The Victor Miller Basis

This module contains functions for quick calculation of a basis of -expansions for the space of modular forms of level 1 and any weight. The basis returned is the Victor Miller basis, which is the unique basis of elliptic modular forms 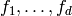for which 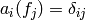for 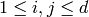(where is the dimension of the space).

This basis is calculated using a standard set of generators for the ring of modular forms, using the fast multiplication algorithms for polynomials and power series provided by the FLINT library. (This is far quicker than using modular symbols).

TESTS:

sage: ModularSymbols(1, 36, 1).cuspidal_submodule().q_expansion_basis(30) == victor_miller_basis(36, 30, cusp_only=True)
True

sage.modular.modform.vm_basis.delta_qexp(prec=10, var='q', K=Integer Ring)

Return the -expansion of the weight 12 cusp form 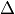as a power series with coefficients in the ring K (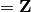 by default).

INPUT:

• prec – integer (default 10), the absolute precision of the output (must be positive)
• var – string (default: ‘q’), variable name
• K – ring (default: ), base ring of answer

OUTPUT:

a power series over K in the variable var

ALGORITHM:

Compute the theta series

a very simple explicit modular form whose 8th power is . Then compute the 8th power using FLINT polynomial arithmetic, which is very fast. (Note that all computations are done over , and coerced into the given coefficient ring afterwards.)

EXAMPLES:

sage: delta_qexp(7)
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 - 6048*q^6 + O(q^7)
sage: delta_qexp(7,'z')
z - 24*z^2 + 252*z^3 - 1472*z^4 + 4830*z^5 - 6048*z^6 + O(z^7)
sage: delta_qexp(-3)
...
ValueError: prec must be positive
sage: delta_qexp(20, K = GF(3))
q + q^4 + 2*q^7 + 2*q^13 + q^16 + 2*q^19 + O(q^20)

AUTHORS:

• William Stein: original code
• David Harvey (2007-05): sped up first squaring step
• Martin Raum (2009-08-02): use FLINT for polynomial arithmetic (instead of NTL)

sage.modular.modform.vm_basis.victor_miller_basis(k, prec=10, cusp_only=False, var='q')

Compute and return the Victor Miller basis for modular forms of weight and level 1 to precision 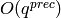. If cusp_only is True, return only a basis for the cuspidal subspace.

INPUT:

• k – an integer
• prec – (default: 10) a positive integer
• cusp_only – bool (default: False)
• var – string (default: ‘q’)

OUTPUT:

A sequence whose entries are power series in ZZ[[var]].

EXAMPLES:

sage: victor_miller_basis(1, 6)
[]
sage: victor_miller_basis(0, 6)
[
1 + O(q^6)
]
sage: victor_miller_basis(2, 6)
[]
sage: victor_miller_basis(4, 6)
[
1 + 240*q + 2160*q^2 + 6720*q^3 + 17520*q^4 + 30240*q^5 + O(q^6)
]

sage: victor_miller_basis(6, 6, var='w')
[
1 - 504*w - 16632*w^2 - 122976*w^3 - 532728*w^4 - 1575504*w^5 + O(w^6)
]

sage: victor_miller_basis(6, 6)
[
1 - 504*q - 16632*q^2 - 122976*q^3 - 532728*q^4 - 1575504*q^5 + O(q^6)
]
sage: victor_miller_basis(12, 6)
[
1 + 196560*q^2 + 16773120*q^3 + 398034000*q^4 + 4629381120*q^5 + O(q^6),
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 + O(q^6)
]

sage: victor_miller_basis(12, 6, cusp_only=True)
[
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 + O(q^6)
]
sage: victor_miller_basis(24, 6, cusp_only=True)
[
q + 195660*q^3 + 12080128*q^4 + 44656110*q^5 + O(q^6),
q^2 - 48*q^3 + 1080*q^4 - 15040*q^5 + O(q^6)
]
sage: victor_miller_basis(24, 6)
[
1 + 52416000*q^3 + 39007332000*q^4 + 6609020221440*q^5 + O(q^6),
q + 195660*q^3 + 12080128*q^4 + 44656110*q^5 + O(q^6),
q^2 - 48*q^3 + 1080*q^4 - 15040*q^5 + O(q^6)
]
sage: victor_miller_basis(32, 6)
[
1 + 2611200*q^3 + 19524758400*q^4 + 19715347537920*q^5 + O(q^6),
q + 50220*q^3 + 87866368*q^4 + 18647219790*q^5 + O(q^6),
q^2 + 432*q^3 + 39960*q^4 - 1418560*q^5 + O(q^6)
]

sage: victor_miller_basis(40,200)[1:] == victor_miller_basis(40,200,cusp_only=True)
True
sage: victor_miller_basis(200,40)[1:] == victor_miller_basis(200,40,cusp_only=True)
True

AUTHORS:

• William Stein, Craig Citro: original code
• Martin Raum (2009-08-02): use FLINT for polynomial arithmetic (instead of NTL)