AUTHORS:
ACKNOWLEDGEMENT: The dimension formulas and implementations in this
module grew out of a program that Bruce Kaskel wrote (around 1996)
in PARI, which Kevin Buzzard subsequently extended. I (William
Stein) then implemented it in C++ for Hecke. I also implemented it
in Magma. Also, the functions for dimensions of spaces with
nontrivial character are based on a paper (that has no proofs) by
Cohen and Oesterle (Springer Lecture notes in math, volume 627,
pages 69-78). The formulas for 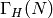 were found
and implemented by Jordi Quer.
were found
and implemented by Jordi Quer.
The formulas here are more complete than in Hecke or Magma.
Currently the input to each function below is an integer and either a Dirichlet
character  or a finite index subgroup of
or a finite index subgroup of 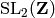 .
If the input is a Dirichlet character
.
If the input is a Dirichlet character  , the dimensions are for
subspaces of
, the dimensions are for
subspaces of 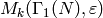 , where
, where  is the modulus of
is the modulus of
 .
.
These functions mostly call the methods dimension_cusp_forms, dimension_modular_forms and so on of the corresponding congruence subgroup classes.
This is used as an intermediate value in computations related to the paper of Cohen-Oesterle.
INPUT:
OUTPUT: element of the base ring of the character
EXAMPLES:
sage: G.<eps> = DirichletGroup(7)
sage: sage.modular.dims.CO_delta(1,5,7,eps^3)
2
This is used as an intermediate value in computations related to the paper of Cohen-Oesterle.
INPUT:
OUTPUT: element of the base ring of the character
EXAMPLES:
sage: G.<eps> = DirichletGroup(7)
sage: G.<eps> = DirichletGroup(7)
sage: sage.modular.dims.CO_nu(1,7,7,eps)
-1
Compute the Cohen-Oesterle function associate to eps,  .
This is a summand in the formula for the dimension of the space of
cusp forms of weight
.
This is a summand in the formula for the dimension of the space of
cusp forms of weight  with character
with character
 .
.
INPUT:
OUTPUT: element of the base ring of eps.
EXAMPLES:
sage: G.<eps> = DirichletGroup(7)
sage: sage.modular.dims.CohenOesterle(eps, 2)
-2/3
sage: sage.modular.dims.CohenOesterle(eps, 4)
-1
The dimension of the space of cusp forms for the given congruence subgroup or Dirichlet character.
INPUT:
EXAMPLES:
sage: dimension_cusp_forms(5,4)
1
sage: dimension_cusp_forms(Gamma0(11),2)
1
sage: dimension_cusp_forms(Gamma1(13),2)
2
sage: dimension_cusp_forms(DirichletGroup(13).0^2,2)
1
sage: dimension_cusp_forms(DirichletGroup(13).0,3)
1
sage: dimension_cusp_forms(Gamma0(11),2)
1
sage: dimension_cusp_forms(Gamma0(11),0)
0
sage: dimension_cusp_forms(Gamma0(1),12)
1
sage: dimension_cusp_forms(Gamma0(1),2)
0
sage: dimension_cusp_forms(Gamma0(1),4)
0
sage: dimension_cusp_forms(Gamma0(389),2)
32
sage: dimension_cusp_forms(Gamma0(389),4)
97
sage: dimension_cusp_forms(Gamma0(2005),2)
199
sage: dimension_cusp_forms(Gamma0(11),1)
0
sage: dimension_cusp_forms(Gamma1(11),2)
1
sage: dimension_cusp_forms(Gamma1(1),12)
1
sage: dimension_cusp_forms(Gamma1(1),2)
0
sage: dimension_cusp_forms(Gamma1(1),4)
0
sage: dimension_cusp_forms(Gamma1(389),2)
6112
sage: dimension_cusp_forms(Gamma1(389),4)
18721
sage: dimension_cusp_forms(Gamma1(2005),2)
159201
sage: dimension_cusp_forms(Gamma1(11),1)
0
sage: e = DirichletGroup(13).0
sage: e.order()
12
sage: dimension_cusp_forms(e,2)
0
sage: dimension_cusp_forms(e^2,2)
1
The dimension of the space of Eisenstein series for the given congruence subgroup.
INPUT:
EXAMPLES:
sage: dimension_eis(5,4)
2
sage: dimension_eis(Gamma0(11),2)
1
sage: dimension_eis(Gamma1(13),2)
11
sage: dimension_eis(Gamma1(2006),2)
3711
sage: e = DirichletGroup(13).0
sage: e.order()
12
sage: dimension_eis(e,2)
0
sage: dimension_eis(e^2,2)
2
sage: e = DirichletGroup(13).0
sage: e.order()
12
sage: dimension_eis(e,2)
0
sage: dimension_eis(e^2,2)
2
sage: dimension_eis(e,13)
2
sage: G = DirichletGroup(20)
sage: dimension_eis(G.0,3)
4
sage: dimension_eis(G.1,3)
6
sage: dimension_eis(G.1^2,2)
6
sage: G = DirichletGroup(200)
sage: e = prod(G.gens(), G(1))
sage: e.conductor()
200
sage: dimension_eis(e,2)
4
sage: dimension_modular_forms(Gamma1(4), 11)
6
The dimension of the space of cusp forms for the given congruence
subgroup (either 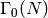 ,
, 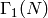 , or
, or
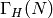 ) or Dirichlet character.
) or Dirichlet character.
INPUT:
EXAMPLES:
sage: dimension_modular_forms(Gamma0(11),2)
2
sage: dimension_modular_forms(Gamma0(11),0)
1
sage: dimension_modular_forms(Gamma1(13),2)
13
sage: dimension_modular_forms(GammaH(11, [10]), 2)
10
sage: dimension_modular_forms(GammaH(11, [10]))
10
sage: dimension_modular_forms(GammaH(11, [10]), 4)
20
sage: e = DirichletGroup(20).1
sage: dimension_modular_forms(e,3)
9
sage: dimension_cusp_forms(e,3)
3
sage: dimension_eis(e,3)
6
sage: dimension_modular_forms(11,2)
2
Return the dimension of the new (or  -new) subspace of
cusp forms for the character or group
-new) subspace of
cusp forms for the character or group  .
.
INPUT:
EXAMPLES:
sage: dimension_new_cusp_forms(100,2)
1
sage: dimension_new_cusp_forms(Gamma0(100),2)
1
sage: dimension_new_cusp_forms(Gamma0(100),4)
5
sage: dimension_new_cusp_forms(Gamma1(100),2)
141
sage: dimension_new_cusp_forms(Gamma1(100),4)
463
sage: dimension_new_cusp_forms(DirichletGroup(100).1^2,2)
2
sage: dimension_new_cusp_forms(DirichletGroup(100).1^2,4)
8
sage: sum(dimension_new_cusp_forms(e,3) for e in DirichletGroup(30))
12
sage: dimension_new_cusp_forms(Gamma1(30),3)
12
Return the Eisenstein number  which is the numerator of
which is the numerator of
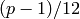 .
.
INPUT:
OUTPUT: Integer
EXAMPLES:
sage: [(p,sage.modular.dims.eisen(p)) for p in prime_range(24)]
[(2, 1), (3, 1), (5, 1), (7, 1), (11, 5), (13, 1), (17, 4), (19, 3), (23, 11)]
Returns the Sturm bound for modular forms with given level and weight. For more details, see the documentation for the sturm_bound method of sage.modular.arithgroup.CongruenceSubgroup objects.
INPUT:
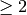 (default: 2)
(default: 2)EXAMPLES:
sage: sturm_bound(11,2)
2
sage: sturm_bound(389,2)
65
sage: sturm_bound(1,12)
1
sage: sturm_bound(100,2)
30
sage: sturm_bound(1,36)
3
sage: sturm_bound(11)
2