Conjectural Slopes of Hecke Polynomial

Interface to Kevin Buzzard’s PARI program for computing conjectural slopes of characteristic polynomials of Hecke operators.

AUTHORS:

• William Stein (2006-03-05): Sage interface
• Kevin Buzzard: PARI program that implements underlying functionality

sage.modular.buzzard.buzzard_tpslopes(p, N, kmax)

Returns a vector of length kmax, whose ‘th entry (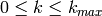) is the conjectural sequence of valuations of eigenvalues of 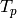on forms of level , weight , and trivial character.

This conjecture is due to Kevin Buzzard, and is only made assuming that does not divide and if is 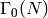-regular.

EXAMPLES:

sage: c = buzzard_tpslopes(2,1,50)
sage: c[50]
[4, 8, 13]

Hence Buzzard would conjecture that the -adic valuations of the eigenvalues of 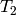on cusp forms of level 1 and weight are , which indeed they are, as one can verify by an explicit computation using, e.g., modular symbols:

sage: M = ModularSymbols(1,50, sign=1).cuspidal_submodule()
sage: T = M.hecke_operator(2)
sage: f = T.charpoly('x')
sage: f.newton_slopes(2)
[13, 8, 4]

AUTHORS:

• Kevin Buzzard: several GP/PARI scripts
• William Stein (2006-03-17): small Sage wrapper of Buzzard’s scripts

sage.modular.buzzard.gp()

Return a copy of the GP interpreter with the appropriate files loaded.

EXAMPLE:

sage: sage.modular.buzzard.gp()
GP/PARI interpreter