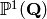 of cusps¶
of cusps¶EXAMPLES:
sage: Cusps
Set P^1(QQ) of all cusps
sage: Cusp(oo)
Infinity
Bases: sage.structure.element.Element
A cusp.
A cusp is either a rational number or infinity, i.e., an element of the projective line over Q. A Cusp is stored as a pair (a,b), where gcd(a,b)=1 and a,b are of type Integer.
EXAMPLES:
sage: a = Cusp(2/3); b = Cusp(oo)
sage: a.parent()
Set P^1(QQ) of all cusps
sage: a.parent() is b.parent()
True
Return g(self), where g=[a,b,c,d] is a list of length 4, which we view as a linear fractional transformation.
EXAMPLES: Apply the identity matrix:
sage: Cusp(0).apply([1,0,0,1])
0
sage: Cusp(0).apply([0,-1,1,0])
Infinity
sage: Cusp(0).apply([1,-3,0,1])
-3
Return the denominator of the cusp a/b.
EXAMPLES:
sage: x=Cusp(6,9); x
2/3
sage: x.denominator()
3
sage: Cusp(oo).denominator()
0
sage: Cusp(-5/10).denominator()
2
Suppose this cusp is  ,
,  is a congruence subgroup of
level
is a congruence subgroup of
level  , and
, and 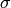 is the automorphism in the Galois
group of
is the automorphism in the Galois
group of 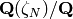 that sends
that sends 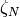 to
to
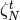 . Then this function computes a cusp
. Then this function computes a cusp 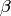 such
that
such
that ![\sigma([\alpha]) = [\beta]](../../_images/math/b8560c4e8d4b3d2f06823c9d7d563a57996939e7.png) , where
, where ![[\alpha]](../../_images/math/d4cda6e2d953f7f4186fa3c8e743caf6bf116ab6.png) is the
equivalence class of
is the
equivalence class of  modulo
modulo  .
.
INPUT:
– integer that is coprime to N
– positive integer (level)
OUTPUT:
- a cusp
EXAMPLES:
sage: Cusp(1/10).galois_action(3, 50)
1/170
sage: Cusp(oo).galois_action(3, 50)
Infinity
sage: Cusp(0).galois_action(3, 50)
0
Here we compute explicitly the permutations of the action for t=3 on cusps for Gamma0(50):
sage: N = 50; t=3; G = Gamma0(N); C = G.cusps()
sage: cl = lambda z: exists(C, lambda y:y.is_gamma0_equiv(z, N))[1]
sage: for i in range(5): print i, t^i, [cl(alpha.galois_action(t^i,N)) for alpha in C]
0 1 [0, 1/25, 1/10, 1/5, 3/10, 2/5, 1/2, 3/5, 7/10, 4/5, 9/10, Infinity]
1 3 [0, 1/25, 7/10, 2/5, 1/10, 4/5, 1/2, 1/5, 9/10, 3/5, 3/10, Infinity]
2 9 [0, 1/25, 9/10, 4/5, 7/10, 3/5, 1/2, 2/5, 3/10, 1/5, 1/10, Infinity]
3 27 [0, 1/25, 3/10, 3/5, 9/10, 1/5, 1/2, 4/5, 1/10, 2/5, 7/10, Infinity]
4 81 [0, 1/25, 1/10, 1/5, 3/10, 2/5, 1/2, 3/5, 7/10, 4/5, 9/10, Infinity]
REFERENCES:
- Section 1.3 of Glenn Stevens, “Arithmetic on Modular Curves”
- There is a long comment about our algorithm in the source code for this function.
 must fit in a long long, i.e., there
must fit in a long long, i.e., thereAUTHORS:
- William Stein, 2009-04-18
Return whether self and other are equivalent modulo the action of
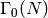 via linear fractional transformations.
via linear fractional transformations.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = Cusp(2,3)
sage: y = Cusp(4,5)
sage: x.is_gamma0_equiv(y, 2)
True
sage: x.is_gamma0_equiv(y, 2, True)
(True, 1)
sage: x.is_gamma0_equiv(y, 3)
False
sage: x.is_gamma0_equiv(y, 3, True)
(False, None)
sage: Cusp(1,0)
Infinity
sage: z = Cusp(1,0)
sage: x.is_gamma0_equiv(z, 3, True)
(True, 2)
ALGORITHM: See Proposition 2.2.3 of Cremona’s book “Algorithms for Modular Elliptic Curves”, or Prop 2.27 of Stein’s Ph.D. thesis.
Return whether self and other are equivalent modulo the action of Gamma_1(N) via linear fractional transformations.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = Cusp(2,3)
sage: y = Cusp(4,5)
sage: x.is_gamma1_equiv(y,2)
(True, 1)
sage: x.is_gamma1_equiv(y,3)
(False, 0)
sage: z = Cusp(QQ(x) + 10)
sage: x.is_gamma1_equiv(z,10)
(True, 1)
sage: z = Cusp(1,0)
sage: x.is_gamma1_equiv(z, 3)
(True, -1)
sage: Cusp(0).is_gamma1_equiv(oo, 1)
(True, 1)
sage: Cusp(0).is_gamma1_equiv(oo, 3)
(False, 0)
Return a pair (b, t), where b is True or False as self and other are equivalent under the action of G, and t is 1 or -1, as described below.
Two cusps 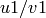 and
and 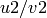 are equivalent modulo
Gamma_H(N) if and only if
are equivalent modulo
Gamma_H(N) if and only if 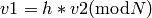 and
and
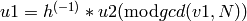 or
or
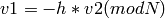 and
and
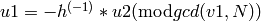 for some
for some
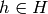 . Then t is 1 or -1 as c and c’ fall into the
first or second case, respectively.
. Then t is 1 or -1 as c and c’ fall into the
first or second case, respectively.
INPUT:
OUTPUT:
EXAMPLES:
sage: x = Cusp(2,3)
sage: y = Cusp(4,5)
sage: x.is_gamma_h_equiv(y,GammaH(13,[2]))
(True, 1)
sage: x.is_gamma_h_equiv(y,GammaH(13,[5]))
(False, 0)
sage: x.is_gamma_h_equiv(y,GammaH(5,[]))
(False, 0)
sage: x.is_gamma_h_equiv(y,GammaH(23,[4]))
(True, -1)
Enumerating the cusps for a space of modular symbols uses this function.
sage: G = GammaH(25,[6]) ; M = G.modular_symbols() ; M
Modular Symbols space of dimension 11 for Congruence Subgroup Gamma_H(25) with H generated by [6] of weight 2 with sign 0 and over Rational Field
sage: M.cusps()
[37/75, 1/2, 31/125, 1/4, -2/5, 2/5, -1/5, 1/10, -3/10, 1/15, 7/15, 9/20]
sage: len(M.cusps())
12
This is always one more than the associated space of weight 2 Eisenstein series.
sage: G.dimension_eis(2)
11
sage: M.cuspidal_subspace()
Modular Symbols subspace of dimension 0 of Modular Symbols space of dimension 11 for Congruence Subgroup Gamma_H(25) with H generated by [6] of weight 2 with sign 0 and over Rational Field
sage: G.dimension_cusp_forms(2)
0
Returns True if this is the cusp infinity.
EXAMPLES:
sage: Cusp(3/5).is_infinity()
False
sage: Cusp(1,0).is_infinity()
True
sage: Cusp(0,1).is_infinity()
False
Return the numerator of the cusp a/b.
EXAMPLES:
sage: x=Cusp(6,9); x
2/3
sage: x.numerator()
2
sage: Cusp(oo).numerator()
1
sage: Cusp(-5/10).numerator()
-1
Bases: sage.structure.parent_base.ParentWithBase
The set of cusps.
EXAMPLES:
sage: C = Cusps; C
Set P^1(QQ) of all cusps
sage: loads(C.dumps()) == C
True