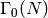Congruence Subgroup $\Gamma_0(N)$ ¶

class sage.modular.arithgroup.congroup_gamma0.Gamma0_class(level)¶

Bases: sage.modular.arithgroup.congroup_gammaH.GammaH_class

The congruence subgroup 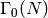$\Gamma_0(N)$ .

TESTS:

sage: Gamma0(11).dimension_cusp_forms(2)
1
sage: a = Gamma0(1).dimension_cusp_forms(2); a
0
sage: type(a)
<type 'sage.rings.integer.Integer'>
sage: Gamma0(5).dimension_cusp_forms(0)
0
sage: Gamma0(20).dimension_cusp_forms(1)
0
sage: Gamma0(20).dimension_cusp_forms(4)
6

sage: Gamma0(23).dimension_cusp_forms(2)
2
sage: Gamma0(1).dimension_cusp_forms(24)
2
sage: Gamma0(3).dimension_cusp_forms(3)
0
sage: Gamma0(11).dimension_cusp_forms(-1)
0

sage: Gamma0(22).dimension_new_cusp_forms()
0
sage: Gamma0(100).dimension_new_cusp_forms(2, 5)
5

Independently compute the dimension 5 above:

sage: m = ModularSymbols(100, 2,sign=1).cuspidal_subspace()
sage: m.new_subspace(5)
Modular Symbols subspace of dimension 5 of Modular Symbols space of dimension 18 for Gamma_0(100) of weight 2 with sign 1 over Rational Field

coset_reps()¶

Return representatives for the right cosets of this congruence subgroup in 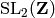${\rm SL}_2(\ZZ)$ as a generator object.

Use list(self.coset_reps()) to obtain coset reps as a list.

EXAMPLES:

sage: list(Gamma0(5).coset_reps())
[[1 0]
[0 1], [ 0 -1]
[ 1  0], [1 0]
[1 1], [ 0 -1]
[ 1  2], [ 0 -1]
[ 1  3], [ 0 -1]
[ 1  4]]
sage: list(Gamma0(4).coset_reps())
 [[1 0] [0 1], 
 [ 0 -1] [ 1  0],
 [1 0] [1 1], 
 [ 0 -1] [ 1  2],
 [ 0 -1] [ 1  3],
 [1 0] [2 1]]
sage: list(Gamma0(1).coset_reps())
[[1 0] [0 1]]

divisor_subgroups()¶

Return the subgroups of SL2Z of the form Gamma0(M) that contain this subgroup, i.e. those for M a divisor of N.

EXAMPLE:

sage: Gamma0(24).divisor_subgroups()
[Modular Group SL(2,Z),
Congruence Subgroup Gamma0(2),
Congruence Subgroup Gamma0(3),
Congruence Subgroup Gamma0(4),
Congruence Subgroup Gamma0(6),
Congruence Subgroup Gamma0(8),
Congruence Subgroup Gamma0(12),
Congruence Subgroup Gamma0(24)]

gamma_h_subgroups()¶

Return the subgroups of the form 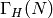$\Gamma_H(N)$ contained in self, where $N$ is the level of self.

EXAMPLES:

sage: G = Gamma0(11)
sage: G.gamma_h_subgroups()
[Congruence Subgroup Gamma_H(11) with H generated by [2], Congruence Subgroup Gamma_H(11) with H generated by [4], Congruence Subgroup Gamma_H(11) with H generated by [10], Congruence Subgroup Gamma_H(11) with H generated by []]
sage: G = Gamma0(12)
sage: G.gamma_h_subgroups()
[Congruence Subgroup Gamma_H(12) with H generated by [5, 7], Congruence Subgroup Gamma_H(12) with H generated by [7], Congruence Subgroup Gamma_H(12) with H generated by [11], Congruence Subgroup Gamma_H(12) with H generated by [5], Congruence Subgroup Gamma_H(12) with H generated by []]

generators(*args, **kwds)¶

Return generators for this congruence subgroup.

The result is cached.

EXAMPLE:

sage: for g in Gamma0(3).generators():
...     print g
...     print '---'
[1 1]
[0 1]
---
[-1  0]
[ 0 -1]
---
...
---
[ 1  0]
[-3  1]
---

index()¶

Return the index of self in the full modular group. This is given by

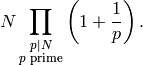
$N \prod_{\substack{p \mid N \\ \text{$p$ prime}}}\left(1 + \frac{1}{p}\right).$

EXAMPLE::: sage: [Gamma0(n).index() for n in [1..19]] [1, 3, 4, 6, 6, 12, 8, 12, 12, 18, 12, 24, 14, 24, 24, 24, 18, 36, 20] sage: Gamma0(32041).index() 32220

is_even()¶

Return True precisely if this subgroup contains the matrix -1.

Since $\Gamma0(N)$ always contains the matrix -1, this always returns True.

EXAMPLES:

sage: Gamma0(12).is_even()
True
sage: SL2Z.is_even()
True

is_subgroup(right)¶

Return True if self is a subgroup of right.

EXAMPLES:

sage: G = Gamma0(20)
sage: G.is_subgroup(SL2Z)
True
sage: G.is_subgroup(Gamma0(4))
True
sage: G.is_subgroup(Gamma0(20))
True
sage: G.is_subgroup(Gamma0(7))
False
sage: G.is_subgroup(Gamma1(20))
False
sage: G.is_subgroup(GammaH(40, []))
False
sage: Gamma0(80).is_subgroup(GammaH(40, [31, 21, 17]))
True
sage: Gamma0(2).is_subgroup(Gamma1(2))
True

ncusps()¶

Return the number of cusps of this subgroup $\Gamma_0(N)$ .

EXAMPLES:

sage: [Gamma0(n).ncusps() for n in [1..19]]
[1, 2, 2, 3, 2, 4, 2, 4, 4, 4, 2, 6, 2, 4, 4, 6, 2, 8, 2]
sage: [Gamma0(n).ncusps() for n in prime_range(2,100)]
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]

nu2()¶

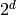Return the number of elliptic points of order 2 for this congruence subgroup $\Gamma_0(N)$ . The number of these is given by a standard formula: 0 if $N$ is divisible by 4 or any prime congruent to -1 mod 4, and otherwise $2^d$ where d is the number of odd primes dividing $N$ .

EXAMPLE:

sage: Gamma0(2).nu2()
1
sage: Gamma0(4).nu2()
0
sage: Gamma0(21).nu2()
0
sage: Gamma0(1105).nu2()
8
sage: [Gamma0(n).nu2() for n in [1..19]]
[1, 1, 0, 0, 2, 0, 0, 0, 0, 2, 0, 0, 2, 0, 0, 0, 2, 0, 0]

nu3()¶

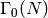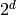Return the number of elliptic points of order 3 for this congruence subgroup $\Gamma_0(N)$ . The number of these is given by a standard formula: 0 if $N$ is divisible by 9 or any prime congruent to -1 mod 3, and otherwise $2^d$ where d is the number of primes other than 3 dividing $N$ .

EXAMPLE:

sage: Gamma0(2).nu3()
0
sage: Gamma0(3).nu3()
1
sage: Gamma0(9).nu3()
0
sage: Gamma0(7).nu3()
2
sage: Gamma0(21).nu3()
2
sage: Gamma0(1729).nu3()
8

sage.modular.arithgroup.congroup_gamma0.Gamma0_constructor(N)¶

Return the congruence subgroup Gamma0(N).

EXAMPLES:

sage: G = Gamma0(51) ; G # indirect doctest
Congruence Subgroup Gamma0(51)
sage: G == Gamma0(51)
True
sage: G is Gamma0(51)
True

sage.modular.arithgroup.congroup_gamma0.is_Gamma0(x)¶

Return True if x is a congruence subgroup of type Gamma0.

EXAMPLES:

sage: from sage.modular.arithgroup.all import is_Gamma0
sage: is_Gamma0(SL2Z)
True
sage: is_Gamma0(Gamma0(13))
True
sage: is_Gamma0(Gamma1(6))
False

Congruence Subgroup $\Gamma_0(N)$ ¶

Previous topic

Next topic

This Page

Navigation

Congruence Subgroup ¶

Previous topic

Next topic

This Page

Quick search

Navigation

Congruence Subgroup $\Gamma_0(N)$ ¶