Arithmetic subgroups defined by permutations

A theorem of Millington states that an arithmetic subgroup of index is uniquely determined by two elements generating a transitive subgroup of the symmetric group 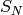and satisfying a certain algebraic relation.

These functions are based on Chris Kurth’s KFarey package.

AUTHORS:

• Chris Kurth (2008): created KFarey package
• David Loeffler (2009): adapted functions from KFarey for inclusion into Sage

class sage.modular.arithgroup.arithgroup_perm.ArithmeticSubgroup_Permutation(L, R)

Bases: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup

An arithmetic subgroup 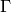defined by two permutations, giving the action of the parabolic generators

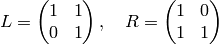
by right multiplication on the coset representatives .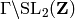

EXAMPLES:

We construct a noncongruence subgroup of index 7 (the smallest possible):

sage: a2 = SymmetricGroup(7)([(1,2),(3,4),(5,6)]); a3 = SymmetricGroup(7)([(1,3,5),(2,6,7)])
sage: G = ArithmeticSubgroup_Permutation(a2*a3, ~a2 * ~a3); G
Arithmetic subgroup corresponding to permutations L=(1,6)(2,3,4,5,7), R=(1,7,6,3,4)(2,5)
sage: G.index()
7
sage: G.dimension_cusp_forms(4)
1
sage: G.is_congruence()
False

We convert some standard congruence subgroups into permutation form:

sage: Gamma0(12).as_permutation_group()
Arithmetic subgroup corresponding to permutations L=(2,3,4,5,6,7,8,9,10,11,12,13)(14,15,16)(17,19,20,18)(21,23,22), R=(1,3,14,17,21,7,24,9,23,20,16,13)(4,18,12)(5,22,11,15)(6,10,19)

The following is the unique index 2 even subgroup of :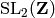

sage: w = SymmetricGroup(2)([2,1])
sage: G = ArithmeticSubgroup_Permutation(w, w)
sage: G.dimension_cusp_forms(6)
1
sage: G.genus()
0

We test unpickling:

sage: G == loads(dumps(G))
True
sage: G is loads(dumps(G))
False

index()

Return the index of self in the full modular group.

EXAMPLE:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.HsuExample18().index()
18

is_congruence()

Return True if this is a congruence subgroup. Uses Hsu’s algorithm, as implemented by Chris Kurth in KFarey.

EXAMPLES:

This example is congruence – it’s Gamma0(3) in disguise:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: G=ap.ArithmeticSubgroup_Permutation(SymmetricGroup(4)((2,3,4)), SymmetricGroup(4)((1,3,4))); G
Arithmetic subgroup corresponding to permutations L=(2,3,4), R=(1,3,4)
sage: G.is_congruence()
True

This one is noncongruence:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.HsuExample10().is_congruence()
False

perm_group()

Return the underlying permutation group.

EXAMPLE:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.HsuExample10().perm_group()
Permutation Group with generators [(1,4)(2,5,9,10,8)(3,7,6), (1,7,9,10,6)(2,3)(4,5,8)]

permutation_action(x)

Given an element x of 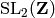, compute the permutation of the cosets of self given by right multiplication by x.

EXAMPLE:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.HsuExample10().permutation_action(SL2Z([32, -21, -67, 44]))
(1,10,5,6,3,8,9,2,7,4)

sage.modular.arithgroup.arithgroup_perm.HsuExample10()

An example of an index 10 arithmetic subgroup studied by Tim Hsu.

EXAMPLE:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.HsuExample10()
Arithmetic subgroup corresponding to permutations L=(1,4)(2,5,9,10,8)(3,7,6), R=(1,7,9,10,6)(2,3)(4,5,8)

sage.modular.arithgroup.arithgroup_perm.HsuExample18()

An example of an index 18 arithmetic subgroup studied by Tim Hsu.

EXAMPLE:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.HsuExample18()
Arithmetic subgroup corresponding to permutations L=(1,2)(3,4)(5,6,7)(8,9,10)(11,12,13,14,15,16,17,18), R=(1,12,18)(2,6,13,9,4,8,17,7)(3,16,14)(5,11)(10,15)

sage.modular.arithgroup.arithgroup_perm.LREvalPerm(w, L, R)

Given a word w as output by sl2z_word_problem, evaluate the word with the given permutations for L and R. Because we are dealing with a right rather than a left action, arguments are evaluated back to front.

EXAMPLE:

sage: import  sage.modular.arithgroup.arithgroup_perm as ap
sage: L = SymmetricGroup(4)('(1,2)(3,4)'); R = SymmetricGroup(4)('(1,2,3,4)')
sage: ap.LREvalPerm([(1,1),(0,1)], L, R) ==  L * R
True

sage.modular.arithgroup.arithgroup_perm.convert_to_permgroup(G)

Given an arbitrary arithmetic subgroup, convert it to permutation form.

Note that the permutation representation is not always unique, so if G is already of permutation type, then the return value won’t necessarily be identical to G, but it will represent the same subgroup.

EXAMPLES:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.convert_to_permgroup(Gamma0(5))
Arithmetic subgroup corresponding to permutations L=(2,3,4,5,6), R=(1,3,5,4,6)
sage: ap.convert_to_permgroup(ap.HsuExample10())
Arithmetic subgroup corresponding to permutations L=(1,2)(3,5,6,7,8)(4,9,10), R=(1,9,6,7,10)(2,5,8)(3,4)

sage.modular.arithgroup.arithgroup_perm.eval_word(B)

Given a word in the format output by sl2z_word_problem, convert it back into an element of SL2(Z).

EXAMPLES:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: ap.eval_word([(0, 1), (1, -1), (0, 0), (1, 3), (0, 2), (1, 9), (0, -1)])
[ 66 -59]
[ 47 -42]

sage.modular.arithgroup.arithgroup_perm.sl2z_word_problem(A, max_iterations=20)

Given an element of SL2Z, express it as a word in the generators L = [1,1,0,1] and R = [1,0,1,1].

The return format is a list of pairs (a,b), where a = 0 or 1 denoting L or R respectively, and b is an integer exponent.

The parameter iterations (default 20) controls the maximum number of iterations to allow in the program’s main loop; an error is raised if the algorithm has not terminated after this many iterations.

EXAMPLE:

sage: import sage.modular.arithgroup.arithgroup_perm as ap
sage: L = SL2Z([1,1,0,1]); R = SL2Z([1,0,1,1])
sage: ap.sl2z_word_problem(L)
[(0, 1)]
sage: ap.sl2z_word_problem(R**(-1))
[(1, -1)]
sage: ap.sl2z_word_problem(L*R)
[(0, 1), (1, -1), (0, 0), (1, 2)]