Dense matrices over the rational field.¶

EXAMPLES:

We create a 3x3 matrix with rational entries and do some operations with it.

sage: a = matrix(QQ, 3,3, [1,2/3, -4/5, 1,1,1, 8,2, -3/19]); a
[    1   2/3  -4/5]
[    1     1     1]
[    8     2 -3/19]
sage: a.det()
2303/285
sage: a.charpoly()
x^3 - 35/19*x^2 + 1259/285*x - 2303/285
sage: b = a^(-1); b
[ -615/2303  -426/2303   418/2303]
[ 2325/2303  1779/2303  -513/2303]
[-1710/2303   950/2303    95/2303]
sage: b.det()
285/2303
sage: a == b
False
sage: a < b
False
sage: b < a
True
sage: a > b
True
sage: a*b
[1 0 0]
[0 1 0]
[0 0 1]

TESTS:

sage: a = matrix(QQ,2,range(4), sparse=False)
sage: TestSuite(a).run()

class sage.matrix.matrix_rational_dense.MatrixWindow¶: Bases: object

class sage.matrix.matrix_rational_dense.Matrix_rational_dense¶

Bases: sage.matrix.matrix_dense.Matrix_dense

antitranspose()¶

Returns the antitranspose of self, without changing self.

EXAMPLES:

sage: A = matrix(QQ,2,3,range(6))
sage: type(A)
<type 'sage.matrix.matrix_rational_dense.Matrix_rational_dense'>
sage: A.antitranspose()
[5 2]
[4 1]
[3 0]
sage: A
[0 1 2]
[3 4 5]

sage: A.subdivide(1,2); A
[0 1|2]
[---+-]
[3 4|5]
sage: A.antitranspose()
[5|2]
[-+-]
[4|1]
[3|0]

change_ring(R)¶

Create the matrix over R with entries the entries of self coerced into R.

EXAMPLES:

sage: a = matrix(QQ,2,[1/2,-1,2,3])
sage: a.change_ring(GF(3))
[2 2]
[2 0]
sage: a.change_ring(ZZ)
...
TypeError: matrix has denominators so can't change to ZZ.
sage: b = a.change_ring(QQ['x']); b
[1/2  -1]
[  2   3]
sage: b.parent()
Full MatrixSpace of 2 by 2 dense matrices over Univariate Polynomial Ring in x over Rational Field

TESTS:

Make sure that subdivisions are preserved when changing rings:

sage: a = matrix(QQ, 3, range(9))
sage: a.subdivide(2,1); a
[0|1 2]
[3|4 5]
[-+---]
[6|7 8]
sage: a.change_ring(ZZ).change_ring(QQ)
[0|1 2]
[3|4 5]
[-+---]
[6|7 8]
sage: a.change_ring(GF(3))
[0|1 2]
[0|1 2]
[-+---]
[0|1 2]

charpoly(var='x', algorithm='linbox')¶

Return the characteristic polynomial of this matrix.

INPUT:

var - ‘x’ (string)
algorithm - ‘linbox’ (default) or ‘generic’

OUTPUT: a polynomial over the rational numbers.

EXAMPLES:

sage: a = matrix(QQ, 3, [4/3, 2/5, 1/5, 4, -3/2, 0, 0, -2/3, 3/4])
sage: f = a.charpoly(); f
x^3 - 7/12*x^2 - 149/40*x + 97/30
sage: f(a)
[0 0 0]
[0 0 0]
[0 0 0]

column(i, from_list=False)¶

Return the i-th column of this matrix as a dense vector.

INPUT:

i - integer
from_list - ignored

EXAMPLES:

sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).column(1)
(-2/3, 4/9)
sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).column(1,from_list=True)
(-2/3, 4/9)
sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).column(-1)
(-2/3, 4/9)
sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).column(-2)
(1/5, 3/4)

decomposition(is_diagonalizable=False, dual=False, algorithm='default', height_guess=None, proof=None)¶

Returns the decomposition of the free module on which this matrix A acts from the right (i.e., the action is x goes to x A), along with whether this matrix acts irreducibly on each factor. The factors are guaranteed to be sorted in the same way as the corresponding factors of the characteristic polynomial.

Let A be the matrix acting from the on the vector space V of column vectors. Assume that A is square. This function computes maximal subspaces W_1, ..., W_n corresponding to Galois conjugacy classes of eigenvalues of A. More precisely, let f(X) be the characteristic polynomial of A. This function computes the subspace 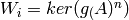$W_i = ker(g_(A)^n)$ , where g_i(X) is an irreducible factor of f(X) and g_i(X) exactly divides f(X). If the optional parameter is_diagonalizable is True, then we let W_i = ker(g(A)), since then we know that ker(g(A)) = 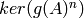$ker(g(A)^n)$ .

If dual is True, also returns the corresponding decomposition of V under the action of the transpose of A. The factors are guaranteed to correspond.

INPUT:

is_diagonalizable - ignored
dual - whether to also return decompositions for the dual
algorithm
- ‘default’: use default algorithm for computing Echelon forms
- ‘multimodular’: much better if the answers factors have small height
height_guess - positive integer; only used by the multimodular algorithm
proof - bool or None (default: None, see proof.linear_algebra or sage.structure.proof); only used by the multimodular algorithm. Note that the Sage global default is proof=True.

Note

IMPORTANT: If you expect that the subspaces in the answer are spanned by vectors with small height coordinates, use algorithm=’multimodular’ and height_guess=1; this is potentially much faster than the default. If you know for a fact the answer will be very small, use algorithm=’multimodular’, height_guess=bound on height, proof=False.

You can get very very fast decomposition with proof=False.

EXAMPLES:

sage: a = matrix(QQ,3,[1..9])
sage: a.decomposition()
[
(Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2  1], True),
(Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[ 1  0 -1]
[ 0  1  2], True)
]

denominator()¶

Return the denominator of this matrix.

OUTPUT: a Sage Integer

EXAMPLES:

sage: b = matrix(QQ,2,range(6)); b[0,0]=-5007/293; b
[-5007/293         1         2]
[        3         4         5]
sage: b.denominator()
293

determinant(algorithm='default', proof=None)¶

Return the determinant of this matrix.

INPUT:

proof - bool or None; if None use proof.linear_algebra(); only relevant for the padic algorithm.
algorithm:

“default” – use PARI for up to 7 rows, then use integer

“pari” – use PARI

“integer” – clear denominators and call det on integer matrix

Note

It would be VERY VERY hard for det to fail even with proof=False.

ALGORITHM: Clear denominators and call the integer determinant function.

EXAMPLES:

sage: m = matrix(QQ,3,[1,2/3,4/5, 2,2,2, 5,3,2/5])
sage: m.determinant()
-34/15
sage: m.charpoly()
x^3 - 17/5*x^2 - 122/15*x + 34/15

echelon_form(algorithm, height_guess='default', proof=None, **kwds=None)¶

INPUT:

algorithm
- ‘default’ (default): use heuristic choice
- ‘padic’: an algorithm based on the IML p-adic solver.
- ‘multimodular’: uses a multimodular algorithm the uses linbox modulo many primes.
- ‘classical’: just clear each column using Gauss elimination
height_guess, **kwds - all passed to the multimodular algorithm; ignored by the p-adic algorithm.
proof - bool or None (default: None, see proof.linear_algebra or sage.structure.proof). Passed to the multimodular algorithm. Note that the Sage global default is proof=True.

OUTPUT: self is no in reduced row echelon form.

EXAMPLES:

sage: a = matrix(QQ, 4, range(16)); a[0,0] = 1/19; a[0,1] = 1/5; a
[1/19  1/5    2    3]
[   4    5    6    7]
[   8    9   10   11]
[  12   13   14   15]
sage: a.echelon_form()
[      1       0       0 -76/157]
[      0       1       0  -5/157]
[      0       0       1 238/157]
[      0       0       0       0]
sage: a.echelon_form(algorithm='multimodular')
[      1       0       0 -76/157]
[      0       1       0  -5/157]
[      0       0       1 238/157]
[      0       0       0       0]

echelonize(algorithm, height_guess='default', proof=None, **kwds=None)¶

INPUT:

algorithm

‘default’ (default): use heuristic choice

‘padic’: an algorithm based on the IML p-adic solver.

‘multimodular’: uses a multimodular algorithm the uses linbox modulo many primes.

‘classical’: just clear each column using Gauss elimination

height_guess, **kwds - all passed to the multimodular algorithm; ignored by the p-adic algorithm.
proof - bool or None (default: None, see proof.linear_algebra or sage.structure.proof). Passed to the multimodular algorithm. Note that the Sage global default is proof=True.

OUTPUT:

matrix - the reduced row echelon for of self.

EXAMPLES:

sage: a = matrix(QQ, 4, range(16)); a[0,0] = 1/19; a[0,1] = 1/5; a
[1/19  1/5    2    3]
[   4    5    6    7]
[   8    9   10   11]
[  12   13   14   15]
sage: a.echelonize(); a
[      1       0       0 -76/157]
[      0       1       0  -5/157]
[      0       0       1 238/157]
[      0       0       0       0]

sage: a = matrix(QQ, 4, range(16)); a[0,0] = 1/19; a[0,1] = 1/5
sage: a.echelonize(algorithm='multimodular'); a
[      1       0       0 -76/157]
[      0       1       0  -5/157]
[      0       0       1 238/157]
[      0       0       0       0]

height()¶

Return the height of this matrix, which is the maximum of the absolute values of all numerators and denominators of entries in this matrix.

OUTPUT: an Integer

EXAMPLES:

sage: b = matrix(QQ,2,range(6)); b[0,0]=-5007/293; b
[-5007/293         1         2]
[        3         4         5]
sage: b.height()
5007

invert(check_invertible=True, algorithm='default')¶

Compute the inverse of this matrix.

Warning

This function is deprecated. Use inverse instead.

EXAMPLES:

sage: a = matrix(QQ,3,range(9))
sage: a.invert()
...
ZeroDivisionError: input matrix must be nonsingular

minpoly(var='x', algorithm='linbox')¶

Return the minimal polynomial of this matrix.

INPUT:

var - ‘x’ (string)
algorithm - ‘linbox’ (default) or ‘generic’

OUTPUT: a polynomial over the rational numbers.

EXAMPLES:

sage: a = matrix(QQ, 3, [4/3, 2/5, 1/5, 4, -3/2, 0, 0, -2/3, 3/4])
sage: f = a.minpoly(); f           
x^3 - 7/12*x^2 - 149/40*x + 97/30
sage: a = Mat(ZZ,4)(range(16))
sage: f = a.minpoly(); f.factor()  
x * (x^2 - 30*x - 80)
sage: f(a) == 0                    
True

sage: a = matrix(QQ, 4, [1..4^2])
sage: factor(a.minpoly())
x * (x^2 - 34*x - 80)
sage: factor(a.minpoly('y'))
y * (y^2 - 34*y - 80)
sage: factor(a.charpoly())
x^2 * (x^2 - 34*x - 80)
sage: b = matrix(QQ, 4, [-1, 2, 2, 0, 0, 4, 2, 2, 0, 0, -1, -2, 0, -4, 0, 4])
sage: a = matrix(QQ, 4, [1, 1, 0,0, 0,1,0,0, 0,0,5,0, 0,0,0,5])
sage: c = b^(-1)*a*b
sage: factor(c.minpoly())
(x - 5) * (x - 1)^2
sage: factor(c.charpoly())
(x - 5)^2 * (x - 1)^2

prod_of_row_sums(cols)¶

randomize(density=1, num_bound=2, den_bound=2, distribution=None, nonzero=False)¶

Randomize density proportion of the entries of this matrix, leaving the rest unchanged.

If x and y are given, randomized entries of this matrix have numerators and denominators bounded by x and y and have density 1.

INPUT:

density - number between 0 and 1 (default: 1)
num_bound - numerator bound (default: 2)
den_bound - denominator bound (default: 2)
distribution - None or ‘1/n’ (default: None); if ‘1/n’ then num_bound, den_bound are ignored and numbers are chosen using the GMP function mpq_randomize_entry_recip_uniform
nonzero - Bool (default: False); whether the new entries are forced to be non-zero

OUTPUT:

None, the matrix is modified in-space

EXAMPLES:

sage: a = matrix(QQ,2,4); a.randomize(); a
[ 0 -1  2 -2]
[ 1 -1  2  1]
sage: a = matrix(QQ,2,4); a.randomize(density=0.5); a
[ -1  -2   0   0]
[  0   0 1/2   0]
sage: a = matrix(QQ,2,4); a.randomize(num_bound=100, den_bound=100); a
[ 14/27  21/25  43/42 -48/67]
[-19/55  64/67 -11/51     76]
sage: a = matrix(QQ,2,4); a.randomize(distribution='1/n'); a
[      3     1/9     1/2     1/4]
[      1    1/39       2 -1955/2]

rank()¶

Return the rank of this matrix.

EXAMPLES::: sage: matrix(QQ,3,[1..9]).rank() 2 sage: matrix(QQ,100,[1..100^2]).rank() 2

right_kernel(algorithm, **kwds='padic')¶

Return the right kernel of this matrix, as a vector space over QQ. For a left kernel use self.left_kernel() or just self.kernel().

INPUT:

algorithm - ‘padic’ (or ‘default’): use IML’s p-adic nullspace algorithm
anything else - passed on to the generic echelon-form based algorithm.
**kwds - passed onto to echelon form algorithm in the echelon case.

EXAMPLES:

A non-trivial right kernel over the rationals::

    sage: A = matrix(QQ, [[2,1,-5,-8],[-1,-1,4,6],[1,0,-1,-2]])
    sage: A.right_kernel()
    Vector space of degree 4 and dimension 2 over Rational Field
    Basis matrix:
    [   1    0   -2  3/2]
    [   0    1    1 -1/2]

A trivial right kernel, plus left kernel (via superclass)::

    sage: M=Matrix(QQ,[[1/2,3],[0,1],[1,1]])
    sage: M.right_kernel()
    Vector space of degree 2 and dimension 0 over Rational Field
    Basis matrix:
    []
    sage: M.left_kernel()
    Vector space of degree 3 and dimension 1 over Rational Field
    Basis matrix:
    [   1 -5/2 -1/2]

row(i, from_list=False)¶

Return the i-th row of this matrix as a dense vector.

INPUT:

i - integer
from_list - ignored

EXAMPLES:

sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).row(1)
(3/4, 4/9)
sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).row(1,from_list=True)
(3/4, 4/9)
sage: matrix(QQ,2,[1/5,-2/3,3/4,4/9]).row(-2)
(1/5, -2/3)

set_row_to_multiple_of_row(i, j, s)¶

Set row i equal to s times row j.

EXAMPLES:

sage: a = matrix(QQ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.set_row_to_multiple_of_row(1,0,-3)
sage: a
[ 0  1  2]
[ 0 -3 -6]

transpose()¶

Returns the transpose of self, without changing self.

EXAMPLES:

We create a matrix, compute its transpose, and note that the original matrix is not changed.

sage: A = matrix(QQ,2,3,xrange(6))
sage: type(A)
<type 'sage.matrix.matrix_rational_dense.Matrix_rational_dense'>
sage: B = A.transpose()
sage: print B
[0 3]
[1 4]
[2 5]
sage: print A
[0 1 2]
[3 4 5]

sage: A.subdivide(None, 1); A
[0|1 2]
[3|4 5]
sage: A.transpose()
[0 3]
[---]
[1 4]
[2 5]

sage.matrix.matrix_rational_dense.clear_mpz_globals()¶

sage.matrix.matrix_rational_dense.gmp_randrange(n1, n2)¶

sage.matrix.matrix_rational_dense.init_mpz_globals()¶

Dense matrices over the rational field.¶

Previous topic

Next topic

This Page

Navigation

Dense matrices over the rational field.¶

Previous topic

Next topic

This Page

Quick search

Navigation