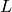Watkins Symmetric Power -function Calculator

SYMPOW is a package to compute special values of symmetric power elliptic curve L-functions. It can compute up to about 64 digits of precision. This interface provides complete access to sympow, which is a standard part of Sage (and includes the extra data files).

Note

Each call to sympow runs a complete sympow process. This incurs about 0.2 seconds overhead.

AUTHORS:

• Mark Watkins (2005-2006): wrote and released sympow
• William Stein (2006-03-05): wrote Sage interface

ACKNOWLEDGEMENT (from sympow readme):

• The quad-double package was modified from David Bailey’s package: http://crd.lbl.gov/~dhbailey/mpdist/
• The squfof implementation was modified from Allan Steel’s version of Arjen Lenstra’s original LIP-based code.
• The ec_ap code was originally written for the kernel of MAGMA, but was modified to use small integers when possible.
• SYMPOW was originally developed using PARI, but due to licensing difficulties, this was eliminated. SYMPOW also does not use the standard math libraries unless Configure is run with the -lm option. SYMPOW still uses GP to compute the meshes of inverse Mellin transforms (this is done when a new symmetric power is added to datafiles).

class sage.lfunctions.sympow.Sympow

Bases: sage.structure.sage_object.SageObject

Watkins Symmetric Power 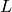-function Calculator

Type sympow.[tab] for a list of useful commands that are implemented using the command line interface, but return objects that make sense in Sage.

You can also use the complete command-line interface of sympow via this class. Type sympow.help() for a list of commands and how to call them.

L(E, n, prec)

Return 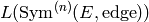to prec digits of precision, where edge is the right edge. Here must be even.

INPUT:

• E - elliptic curve
• n - even integer
• prec - integer

OUTPUT:

• string - real number to prec digits of precision as a string.

Note

Before using this function for the first time for a given , you may have to type sympow('-new_data n'), where n is replaced by your value of .

If you would like to see the extensive output sympow prints when running this function, just type set_verbose(2).

EXAMPLES:

sage: a = sympow.L(EllipticCurve('11a'), 2, 16); a   # optional
'1.057599244590958E+00'
sage: RR(a)                    # optional -- requires precomputations
1.05759924459096

Lderivs(E, n, prec, d)

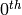Return to 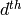derivatives of 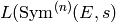to prec digits of precision, where is the right edge if is even and the center if is odd.

INPUT:

• E - elliptic curve
• n - integer (even or odd)
• prec - integer
• d - integer

OUTPUT: a string, exactly as output by sympow

Note

To use this function you may have to run a few commands like sympow('-new_data 1d2'), each which takes a few minutes. If this function fails it will indicate what commands have to be run.

EXAMPLES:

sage: print sympow.Lderivs(EllipticCurve('11a'), 1, 16, 2)  # not tested
...
 1n0: 2.538418608559107E-01
 1w0: 2.538418608559108E-01
 1n1: 1.032321840884568E-01
 1w1: 1.059251499158892E-01
 1n2: 3.238743180659171E-02
 1w2: 3.414818600982502E-02

analytic_rank(E)

Return the analytic rank and leading 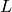-value of the elliptic curve .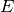

INPUT:

• E - elliptic curve over Q

OUTPUT:

• integer - analytic rank
• string - leading coefficient (as string)

Note

The analytic rank is not computed provably correctly in general.

Note

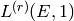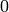In computing the analytic rank we consider to be if .

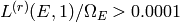EXAMPLES: We compute the analytic ranks of the lowest known conductor curves of the first few ranks:

sage: sympow.analytic_rank(EllipticCurve('11a'))
(0, '2.53842e-01')
sage: sympow.analytic_rank(EllipticCurve('37a'))
(1, '3.06000e-01')
sage: sympow.analytic_rank(EllipticCurve('389a'))
(2, '7.59317e-01')
sage: sympow.analytic_rank(EllipticCurve('5077a'))
(3, '1.73185e+00')
sage: sympow.analytic_rank(EllipticCurve([1, -1, 0, -79, 289]))
(4, '8.94385e+00')
sage: sympow.analytic_rank(EllipticCurve([0, 0, 1, -79, 342]))  # long
(5, '3.02857e+01')
sage: sympow.analytic_rank(EllipticCurve([1, 1, 0, -2582, 48720]))  # long
(6, '3.20781e+02')
sage: sympow.analytic_rank(EllipticCurve([0, 0, 0, -10012, 346900]))  # long
(7, '1.32517e+03')

help()

modular_degree(E)

Return the modular degree of the elliptic curve E, assuming the Stevens conjecture.

INPUT:

• E - elliptic curve over Q

OUTPUT:

• integer - modular degree

EXAMPLES: We compute the modular degrees of the lowest known conductor curves of the first few ranks:

sage: sympow.modular_degree(EllipticCurve('11a'))
1
sage: sympow.modular_degree(EllipticCurve('37a'))
2
sage: sympow.modular_degree(EllipticCurve('389a'))
40
sage: sympow.modular_degree(EllipticCurve('5077a'))
1984
sage: sympow.modular_degree(EllipticCurve([1, -1, 0, -79, 289]))
334976

new_data(n)

Pre-compute data files needed for computation of n-th symmetric powers.