Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- L-Functions »
 -function Calculator¶
-function Calculator¶This a standard part of Sage. This interface provides complete access to Rubinstein’s lcalc calculator with extra PARI functionality compiled in.
Note
Each call to lcalc runs a complete lcalc process. On a typical Linux system, this entails about 0.3 seconds overhead.
AUTHORS:
Bases: sage.structure.sage_object.SageObject
Rubinstein’s  -functions Calculator
-functions Calculator
Type lcalc.[tab] for a list of useful commands that are implemented using the command line interface, but return objects that make sense in Sage. For each command the possible inputs for the L-function are:
 ; defines
; defines 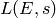
You can also use the complete command-line interface of
Rubinstein’s  -functions calculations program via this
class. Type lcalc.help() for a list of commands and
how to call them.
-functions calculations program via this
class. Type lcalc.help() for a list of commands and
how to call them.
Return the analytic rank of the  -function at the central
critical point.
-function at the central
critical point.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)OUTPUT: integer
Note
Of course this is not provably correct in general, since it is an open problem to compute analytic ranks provably correctly in general.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: lcalc.analytic_rank(E)
1
Return values of 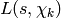 for each quadratic
character
for each quadratic
character 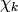 whose discriminant
whose discriminant 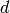 satisfies
satisfies
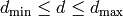 .
.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)OUTPUT:
EXAMPLES:
sage: lcalc.twist_values(0.5, -10, 10)
[(-8, 1.10042141), (-7, 1.14658567), (-4, 0.667691457), (-3, 0.480867558), (5, 0.231750947), (8, 0.373691713)]
Return first  real parts of nontrivial zeros for each
quadratic character
real parts of nontrivial zeros for each
quadratic character 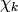 whose discriminant
whose discriminant 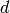 satisfies
satisfies
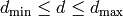 .
.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)OUTPUT:
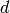 ,
and values are list of corresponding zeros.
,
and values are list of corresponding zeros.EXAMPLES:
sage: lcalc.twist_zeros(3, -3, 6)
{-3: [8.03973716, 11.2492062, 15.7046192], 5: [6.64845335, 9.83144443, 11.9588456]}
Return 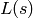 for
for  a complex number.
a complex number.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)EXAMPLES:
sage: I = CC.0
sage: lcalc.value(0.5 + 100*I)
2.69261989 - 0.0203860296*I
Note, Sage can also compute zeta at complex numbers (using the PARI C library):
sage: (0.5 + 100*I).zeta()
2.69261988568132 - 0.0203860296025982*I
Return values of 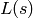 at number_samples
equally-spaced sample points along the line from
at number_samples
equally-spaced sample points along the line from  to
to
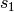 in the complex plane.
in the complex plane.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)OUTPUT:
EXAMPLES:
sage: I = CC.0
sage: lcalc.values_along_line(0.5, 0.5+20*I, 5)
[(0.500000000, -1.46035451), (0.500000000 + 4.00000000*I, 0.606783764 + 0.0911121400*I), (0.500000000 + 8.00000000*I, 1.24161511 + 0.360047588*I), (0.500000000 + 12.0000000*I, 1.01593665 - 0.745112472*I), (0.500000000 + 16.0000000*I, 0.938545408 + 1.21658782*I)]
Sometimes warnings are printed (by lcalc) when this command is run:
sage: E = EllipticCurve('389a')
sage: E.lseries().values_along_line(0.5, 3, 5)
[(0, 0.209951303),
(0.500000000, -...e-16),
(1.00000000, 0.133768433),
(1.50000000, 0.360092864),
(2.00000000, 0.552975867)]
Return the imaginary parts of the first  nontrivial
zeros of the
nontrivial
zeros of the  -function in the upper half plane, as
32-bit reals.
-function in the upper half plane, as
32-bit reals.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)This function also checks the Riemann Hypothesis and makes sure no zeros are missed. This means it looks for several dozen zeros to make sure none have been missed before outputting any zeros at all, so takes longer than self.zeros_of_zeta_in_interval(...).
EXAMPLES:
sage: lcalc.zeros(4) # long
[14.1347251, 21.0220396, 25.0108576, 30.4248761]
sage: lcalc.zeros(5, L='--tau') # long
[9.22237940, 13.9075499, 17.4427770, 19.6565131, 22.3361036]
sage: lcalc.zeros(3, EllipticCurve('37a')) # long
[0.000000000, 5.00317001, 6.87039122]
Return the imaginary parts of (most of) the nontrivial zeros of the
 -function on the line
-function on the line 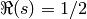 with positive
imaginary part between
with positive
imaginary part between  and
and 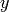 , along with a
technical quantity for each.
, along with a
technical quantity for each.
INPUT:
 -function (default:
Riemann zeta function)
-function (default:
Riemann zeta function)OUTPUT: list of pairs (zero, S(T)).
Rubinstein writes: The first column outputs the imaginary part of
the zero, the second column a quantity related to  (it increases roughly by 2 whenever a sign change, i.e. pair of
zeros, is missed). Higher up the critical strip you should use a
smaller stepsize so as not to miss zeros.
(it increases roughly by 2 whenever a sign change, i.e. pair of
zeros, is missed). Higher up the critical strip you should use a
smaller stepsize so as not to miss zeros.
EXAMPLES:
sage: lcalc.zeros_in_interval(10, 30, 0.1)
[(14.1347251, 0.184672916), (21.0220396, -0.0677893290), (25.0108576, -0.0555872781)]