Basic functionality for dual groups of finite multiplicative Abelian groups

AUTHORS:

• David Joyner (2006-08) (based on abelian_groups)
• David Joyner (2006-10) modifications suggested by William Stein

TODO:

• additive abelian groups should also be supported.

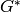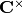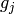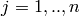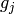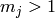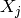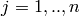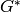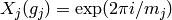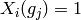The basic idea is very simple. Let G be an abelian group and its dual (i.e., the group of homomorphisms from G to ). Let , , denote generators of - say is of order . There are generators , , of for which and if 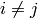. These are used to construct 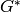in the DualAbelianGroup class below.

Sage supports multiplicative abelian groups on any prescribed finite number 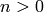of generators. Use the AbelianGroup function to create an abelian group, the DualAbelianGroup function to create its dual, and then the gen and gens functions to obtain the corresponding generators. You can print the generators as arbitrary strings using the optional names argument to the DualAbelianGroup function.

sage.groups.abelian_gps.dual_abelian_group.DualAbelianGroup(G, names='X', base_ring=Complex Field with 53 bits of precision)

Create the dual group of the multiplicative abelian group .

INPUT:

• G - a finite abelian group
• names - (optional) names of generators

OUTPUT: The dual group of G.

EXAMPLES:

sage: F = AbelianGroup(5, [2,5,7,8,9], names='abcde')
sage: (a, b, c, d, e) = F.gens()
sage: Fd = DualAbelianGroup(F,names='ABCDE')
sage: A,B,C,D,E = Fd.gens()
sage: A(a)    ## random
-1.0000000000000000 + 0.00000000000000013834419720915037*I
sage: A(b); A(c); A(d); A(e)
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000

class sage.groups.abelian_gps.dual_abelian_group.DualAbelianGroup_class(G, names='X', bse_ring=None)

Bases: sage.groups.group.AbelianGroup

Dual of abelian group.

EXAMPLES:

sage: F = AbelianGroup(5,[3,5,7,8,9],names = list("abcde"))
sage: DualAbelianGroup(F)
Dual of Abelian Group isomorphic to Z/3Z x Z/5Z x Z/7Z x Z/8Z x Z/9Z  over Complex Field with 53 bits of precision
sage: F = AbelianGroup(4,[15,7,8,9],names = list("abcd"))
sage: DualAbelianGroup(F)
Dual of Abelian Group isomorphic to Z/15Z x Z/7Z x Z/8Z x Z/9Z  over Complex Field with 53 bits of precision

base_ring()

gen(i=0)

The -th generator of the abelian group.

EXAMPLES:

sage: F = AbelianGroup(3,[1,2,3],names='a')
sage: Fd = DualAbelianGroup(F, names="A")
sage: Fd.0
A0
sage: Fd.1
A1
sage: Fd.invariants()
[2, 3]

group()

invariants()

The invariants of the dual group.

EXAMPLES:

sage: F = AbelianGroup(1000)
sage: Fd = DualAbelianGroup(F)
sage: invs = Fd.invariants(); len(invs)
1000

This can be slow for 10000 or more generators.

is_commutative()

Return True since this group is commutative.

EXAMPLES:

sage: G = AbelianGroup([2,3,9])
sage: Gd = DualAbelianGroup(G)
sage: Gd.is_commutative()
True
sage: Gd.is_abelian()
True

list()

Return list of all elements of this group.

EXAMPLES:

sage: G = AbelianGroup([2,3], names = "ab")
sage: Gd = DualAbelianGroup(G, names = "AB")
sage: Gd.list()
[1, B, B^2, A, A*B, A*B^2]

ngens()

The number of generators of the dual group.

EXAMPLES:

sage: F = AbelianGroup(1000)
sage: Fd = DualAbelianGroup(F)
sage: Fd.ngens()
1000

This can be slow for 10000 or more generators.

order()

Return the order of this group.

EXAMPLES:

sage: G = AbelianGroup([2,3,9])
sage: Gd = DualAbelianGroup(G)
sage: Gd.order()
54

random()

Deprecated. Use self.random_element() instead.

random_element()

Return a random element of this dual group.

EXAMPLES:

sage: G = AbelianGroup([2,3,9])
sage: Gd = DualAbelianGroup(G)
sage: Gd.random_element()
X0*X1^2*X2
sage: N = 43^2-1
sage: G = AbelianGroup([N],names="a")
sage: Gd = DualAbelianGroup(G,names="A")
sage: a, = G.gens()
sage: A, = Gd.gens()
sage: x = a^(N/4); y = a^(N/3); z = a^(N/14)
sage: X = Gd.random_element(); X
A^615
sage: len([a for a in [x,y,z] if abs(X(a)-1)>10^(-8)])
2

sage.groups.abelian_gps.dual_abelian_group.is_DualAbelianGroup(x)

Return True if is the dual group of an abelian group.

EXAMPLES:

sage: from sage.groups.abelian_gps.dual_abelian_group import is_DualAbelianGroup
sage: F = AbelianGroup(5,[3,5,7,8,9],names = list("abcde"))
sage: Fd = DualAbelianGroup(F)
sage: is_DualAbelianGroup(Fd)
True
sage: F = AbelianGroup(3,[1,2,3],names='a')
sage: Fd = DualAbelianGroup(F)
sage: Fd.gens()
(X0, X1)
sage: F.gens()
(a0, a1)