Special Linear Groups

AUTHORS:

• William Stein: initial version
• David Joyner (2006-05): added examples, _latex_, __str__, gens, as_matrix_group
• William Stein (2006-12-09): rewrite

EXAMPLES:

sage: SL(2, ZZ)
Special Linear Group of degree 2 over Integer Ring
sage: G = SL(2,GF(3)); G
Special Linear Group of degree 2 over Finite Field of size 3
sage: G.is_finite()
True
sage: G.conjugacy_class_representatives()
[
[1 0]
[0 1],
[0 2]
[1 1],
[0 1]
[2 1],
[2 0]
[0 2],
[0 2]
[1 2],
[0 1]
[2 2],
[0 2]
[1 0]
]
sage: G = SL(6,GF(5))
sage: G.gens()
[
[2 0 0 0 0 0]
[0 3 0 0 0 0]
[0 0 1 0 0 0]
[0 0 0 1 0 0]
[0 0 0 0 1 0]
[0 0 0 0 0 1],
[4 0 0 0 0 1]
[4 0 0 0 0 0]
[0 4 0 0 0 0]
[0 0 4 0 0 0]
[0 0 0 4 0 0]
[0 0 0 0 4 0]
]

sage.groups.matrix_gps.special_linear.SL(n, R, var='a')

Return the special linear group of degree over the ring .

EXAMPLES:

sage: SL(3,GF(2))
Special Linear Group of degree 3 over Finite Field of size 2
sage: G = SL(15,GF(7)); G
Special Linear Group of degree 15 over Finite Field of size 7
sage: G.category()
Category of finite groups
sage: G.order()
1956712595698146962015219062429586341124018007182049478916067369638713066737882363393519966343657677430907011270206265834819092046250232049187967718149558134226774650845658791865745408000000
sage: len(G.gens())
2
sage: G = SL(2,ZZ); G
Special Linear Group of degree 2 over Integer Ring
sage: G.gens()
[
[ 0  1]
[-1  0],
[1 1]
[0 1]
]

Next we compute generators for .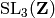

sage: G = SL(3,ZZ); G
Special Linear Group of degree 3 over Integer Ring
sage: G.gens()
[
[0 1 0]
[0 0 1]
[1 0 0],
[ 0  1  0]
[-1  0  0]
[ 0  0  1],
[1 1 0]
[0 1 0]
[0 0 1]
]

sage: TestSuite(G).run()

class sage.groups.matrix_gps.special_linear.SpecialLinearGroup_finite_field(n, R, var='a', category=None)

Bases: sage.groups.matrix_gps.special_linear.SpecialLinearGroup_generic, sage.groups.matrix_gps.matrix_group.MatrixGroup_gap_finite_field

class sage.groups.matrix_gps.special_linear.SpecialLinearGroup_generic(n, R, var='a', category=None)

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.groups.matrix_gps.matrix_group.MatrixGroup_gap