Paraphrased from the GAP manual: The general orthogonal group
 consists of those
consists of those 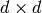 matrices
over the field
matrices
over the field 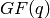 that respect a non-singular
quadratic form specified by
that respect a non-singular
quadratic form specified by  . (Use the GAP command
InvariantQuadraticForm to determine this form explicitly.) The
value of
. (Use the GAP command
InvariantQuadraticForm to determine this form explicitly.) The
value of  must be
must be 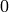 for odd
for odd 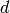 (and
can optionally be omitted in this case), respectively one of
(and
can optionally be omitted in this case), respectively one of
 or
or  for even
for even 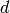 .
.
SpecialOrthogonalGroup returns a group isomorphic to the special
orthogonal group 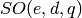 , which is the subgroup of all
those matrices in the general orthogonal group that have
determinant one. (The index of
, which is the subgroup of all
those matrices in the general orthogonal group that have
determinant one. (The index of 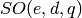 in
in
 is
is  if
if 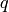 is odd, but
is odd, but
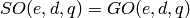 if
if 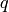 is even.)
is even.)
Warning
GAP notation: GO([e,] d, q), SO([e,] d, q) ([...] denotes and optional value)
Sage notation: GO(d, GF(q), e=0), SO( d, GF(q), e=0)
There is no Python trick I know of to allow the first argument to have the default value e=0 and leave the other two arguments as non-default. This forces us into non-standard notation.
AUTHORS:
Return the general orthogonal group.
EXAMPLES:
Bases: sage.groups.matrix_gps.orthogonal.OrthogonalGroup
EXAMPLES:
sage: GO( 3, GF(7), 0)
General Orthogonal Group of degree 3, form parameter 0, over the Finite Field of size 7
sage: GO( 3, GF(7), 0).order()
672
sage: GO( 3, GF(7), 0).random_element()
[5 1 4]
[1 0 0]
[6 0 1]
This wraps GAP’s command “InvariantQuadraticForm”. From the GAP documentation:
INPUT:
OUTPUT:
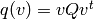 , and the invariance under G is
given by the equation
, and the invariance under G is
given by the equation 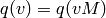 for all
for all
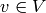 and
and 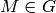 .
.EXAMPLES:
sage: G = GO( 4, GF(7), 1)
sage: G.invariant_quadratic_form()
[0 1 0 0]
[0 0 0 0]
[0 0 3 0]
[0 0 0 1]
Bases: sage.groups.matrix_gps.matrix_group.MatrixGroup_gap
Return the invariant form of this orthogonal group.
TODO: What is the point of this? What does it do? How does it work?
EXAMPLES:
sage: G = SO( 4, GF(7), 1)
sage: G.invariant_form()
1
Return the special orthogonal group of degree  over the
ring
over the
ring 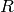 .
.
INPUT:
EXAMPLES:
sage: G = SO(3,GF(5))
sage: G.gens()
[
[2 0 0]
[0 3 0]
[0 0 1],
[3 2 3]
[0 2 0]
[0 3 1],
[1 4 4]
[4 0 0]
[2 0 4]
]
sage: G = SO(3,GF(5))
sage: G.as_matrix_group()
Matrix group over Finite Field of size 5 with 3 generators:
[[[2, 0, 0], [0, 3, 0], [0, 0, 1]], [[3, 2, 3], [0, 2, 0], [0, 3, 1]], [[1, 4, 4], [4, 0, 0], [2, 0, 4]]]
Bases: sage.groups.matrix_gps.orthogonal.OrthogonalGroup
EXAMPLES:
sage: G = SO( 4, GF(7), 1); G
Special Orthogonal Group of degree 4, form parameter 1, over the Finite Field of size 7
sage: G._gap_init_()
'SO(1, 4, 7)'
sage: G.random_element()
[1 2 5 0]
[2 2 1 0]
[1 3 1 5]
[1 3 1 3]
Return the quadratic form 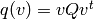 on the space on
which this group
on the space on
which this group 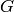 that satisfies the equation
that satisfies the equation
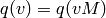 for all
for all 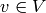 and
and
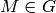 .
.
Note
Uses GAP’s command InvariantQuadraticForm.
OUTPUT:
EXAMPLES:
sage: G = SO( 4, GF(7), 1)
sage: G.invariant_quadratic_form()
[0 1 0 0]
[0 0 0 0]
[0 0 3 0]
[0 0 0 1]