Multivariate Polynomial Systems.¶

We call a finite set of multivariate polynomials an MPolynomialSystem.

In many other computer algebra systems (cf. Singular) this class would be called Ideal but an ideal is a very distinct object from its generators and thus this is not an ideal in Sage.

The idea of polynomial systems is specialized to systems which consist of several “rounds” in Sage. These kind of polynomial systems arise naturally in algebraic cryptanalysis of symmetric cryptographic primitives. The most prominent examples of these systems are: the small scale variants of the AES [CMR05] (cf. mq.SR) and Flurry/Curry [BPW06].

AUTHORS:

Martin Albrecht (2007ff): initial version
Martin Albrecht (2009): refactoring, clean-up, new functions

EXAMPLES:

As an example consider a small scale variant of the AES:

sage: sr = mq.SR(2,1,2,4,gf2=True,polybori=True)
sage: sr
SR(2,1,2,4)

We can construct a polynomial system for a random plaintext-ciphertext pair and study it:

sage: F,s = sr.polynomial_system()
sage: F
Polynomial System with 112 Polynomials in 64 Variables

sage: r2 = F.round(2); r2
(w200 + k100 + x100 + x102 + x103, 
 w201 + k101 + x100 + x101 + x103 + 1, 
 w202 + k102 + x100 + x101 + x102 + 1, 
 w203 + k103 + x101 + x102 + x103, 
 w210 + k110 + x110 + x112 + x113, 
 w211 + k111 + x110 + x111 + x113 + 1, 
 w212 + k112 + x110 + x111 + x112 + 1, 
 w213 + k113 + x111 + x112 + x113, 
 w100*x100 + w100*x103 + w101*x102 + w102*x101 + w103*x100, 
 w100*x100 + w100*x101 + w101*x100 + w101*x103 + w102*x102 + w103*x101, 
 w100*x101 + w100*x102 + w101*x100 + w101*x101 + w102*x100 + w102*x103 + w103*x102, 
 w100*x100 + w100*x101 + w100*x103 + w101*x101 + w102*x100 + w102*x102 + w103*x100 + x100, 
 w100*x102 + w101*x100 + w101*x101 + w101*x103 + w102*x101 + w103*x100 + w103*x102 + x101, 
 w100*x100 + w100*x101 + w100*x102 + w101*x102 + w102*x100 + w102*x101 + w102*x103 + w103*x101 + x102, 
 w100*x101 + w101*x100 + w101*x102 + w102*x100 + w103*x101 + w103*x103 + x103, 
 w100*x100 + w100*x102 + w100*x103 + w101*x100 + w101*x101 + w102*x102 + w103*x100 + w100,
 w100*x101 + w100*x103 + w101*x101 + w101*x102 + w102*x100 + w102*x103 + w103*x101 + w101, 
 w100*x100 + w100*x102 + w101*x100 + w101*x102 + w101*x103 + w102*x100 + w102*x101 + w103*x102 + w102, 
 w100*x101 + w100*x102 + w101*x100 + w101*x103 + w102*x101 + w103*x103 + w103, 
 w100*x102 + w101*x101 + w102*x100 + w103*x103 + 1, 
 w110*x110 + w110*x113 + w111*x112 + w112*x111 + w113*x110, 
 w110*x110 + w110*x111 + w111*x110 + w111*x113 + w112*x112 + w113*x111, 
 w110*x111 + w110*x112 + w111*x110 + w111*x111 + w112*x110 + w112*x113 + w113*x112, 
 w110*x110 + w110*x111 + w110*x113 + w111*x111 + w112*x110 + w112*x112 + w113*x110 + x110, 
 w110*x112 + w111*x110 + w111*x111 + w111*x113 + w112*x111 + w113*x110 + w113*x112 + x111, 
 w110*x110 + w110*x111 + w110*x112 + w111*x112 + w112*x110 + w112*x111 + w112*x113 + w113*x111 + x112, 
 w110*x111 + w111*x110 + w111*x112 + w112*x110 + w113*x111 + w113*x113 + x113, 
 w110*x110 + w110*x112 + w110*x113 + w111*x110 + w111*x111 + w112*x112 + w113*x110 + w110, 
 w110*x111 + w110*x113 + w111*x111 + w111*x112 + w112*x110 + w112*x113 + w113*x111 + w111, 
 w110*x110 + w110*x112 + w111*x110 + w111*x112 + w111*x113 + w112*x110 + w112*x111 + w113*x112 + w112, 
 w110*x111 + w110*x112 + w111*x110 + w111*x113 + w112*x111 + w113*x113 + w113, 
 w110*x112 + w111*x111 + w112*x110 + w113*x113 + 1)

 sage: type(r2)
 <class 'sage.crypto.mq.mpolynomialsystem.MPolynomialRoundSystem_generic'>

As an example, we separate the system in independent subsystems or compute the coefficient matrix:

sage: C = mq.MPolynomialSystem(r2).connected_components(); C
[Polynomial System with 16 Polynomials in 16 Variables, 
 Polynomial System with 16 Polynomials in 16 Variables]

sage: C[0].groebner_basis()
[x111*x110 + w113*x110 + w113*x112 + w113*x113 + w113*w111 + w113*w112 + x111 + x113 + w110 + w111 + w112, 
 x112*x110 + w113*x112 + w113*x113 + w113*w110 + w113*w112 + x110 + x112 + 1, 
 x112*x111 + w113*w110 + x110 + x111 + x113 + w111 + w113, 
 x113*x110 + w113*x110 + w113*x112 + w113*w110 + w113*w111 + w113*w112 + x110 + x111 + x113 + w110 + w111 + 1, 
 x113*x111 + w113*x110 + w113*x112 + w113*x113 + w113*w112 + x111 + x112 + x113 + w111 + w112, 
 x113*x112 + w113*x112 + w113*x113 + w113*w110 + x111 + w110 + w112 + 1, 
 w110*x110 + w113*x110 + w113*w110 + w113*w111 + x110 + x113 + w111 + w112 + 1, 
 w110*x111 + w113*x112 + w113*w110 + w113*w111 + x110 + x112 + x113 + w113, 
 w110*x112 + w113*x110 + w113*x112 + w113*x113 + x112 + x113 + w110 + w111 + w112, 
 w110*x113 + w113*x110 + w113*x113 + x111 + x113 + w111 + w113 + 1, 
 w111*x110 + w113*x110 + w113*x112 + x110 + x111 + w110 + w113 + 1, 
 w111*x111 + w113*x110 + w113*x113 + w113*w110 + w113*w111 + x110 + x111 + x112 + x113, 
 w111*x112 + w113*x110 + w113*x112 + w113*w110 + w113*w111 + x110 + x111 + x112 + w110 + w112, 
 w111*x113 + w113*x113 + w113*w110 + w113*w111 + x111 + x112 + w110 + w111 + w112 + 1, 
 w111*w110 + w113*x110 + w113*x112 + w113*x113 + w113*w111 + w113*w112 + x110 + x111 + x112 + x113 + w111, 
 w112*x110 + w113*x112 + w113*x113 + w113*w110 + w113*w111 + x110 + x111 + w110 + w111 + w112 + 1, 
 w112*x111 + w113*x112 + w113*x113 + x112 + w110 + w113, 
 w112*x112 + w113*x113 + x110 + x111 + w110 + w111 + 1, 
 w112*x113 + w113*x110 + w113*x112 + w113*x113 + w113*w110 + w113*w111 + x111 + x112 + x113 + w110, 
 w112*w110 + w113*x112 + w113*x113 + w113*w110 + w113*w112 + x110 + x111 + x112 + w111 + 1, 
 w112*w111 + w113*x110 + w113*x112 + w113*w110 + w113*w111 + w113*w112 + x110 + w113 + 1, 
 w113*x111 + w113*w110 + w113*w111 + x111 + w110 + w111, 
 w210 + k110 + x110 + x112 + x113, 
 w211 + k111 + x110 + x111 + x113 + 1, 
 w212 + k112 + x110 + x111 + x112 + 1, 
 w213 + k113 + x111 + x112 + x113]

sage: A,v = mq.MPolynomialSystem(r2).coefficient_matrix()
sage: A.rank()
32

Using these building blocks we can implement a simple XL algorithm easily:

sage: sr = mq.SR(1,1,1,4,gf2=True,polybori=True,order='lex')
sage: F,s = sr.polynomial_system()

sage: monomials = [a*b for a in F.variables() for b in F.variables() if a<b]
sage: len(monomials)
190
sage: F2 = mq.MPolynomialSystem(map(mul, cartesian_product_iterator((monomials, F))))
sage: A,v = F2.coefficient_matrix(sparse=False)
sage: A.echelonize()
sage: A
6840 x 4474 dense matrix over Finite Field of size 2 (type 'print A.str()' to see all of the entries)
sage: A.rank()
4056
sage: A[4055]*v
(k002*k003)

The last output tells us that k002 and k003 can’t both be 1.

TEST:

sage: P.<x,y> = PolynomialRing(QQ)
sage: I = [[x^2 + y^2], [x^2 - y^2]]
sage: F = mq.MPolynomialSystem(P,I)
sage: loads(dumps(F)) == F
True

REFERENCES:

[BPW06]

J. Buchmann, A. Pychkine, R.-P. Weinmann Block Ciphers Sensitive to Groebner Basis Attacks in Topics in Cryptology – CT RSA‘06; LNCS 3860; pp. 313–331; Springer Verlag 2006; pre-print available at http://eprint.iacr.org/2005/200

sage.crypto.mq.mpolynomialsystem.MPolynomialRoundSystem(R, gens)¶

Construct an object representing the equations of a single round e.g. of a block cipher or however a “round” is defined.

INPUT:

R - the base ring
gens - list (default: [])

EXAMPLE:

sage: P.<x,y,z> = PolynomialRing(GF(2),3)
sage: mq.MPolynomialRoundSystem(P,[x*y +1, z + 1])
(x*y + 1, z + 1)

class sage.crypto.mq.mpolynomialsystem.MPolynomialRoundSystem_generic(R, gens)¶

Bases: sage.structure.sage_object.SageObject

gens()¶

Return list of polynomials in in the system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: R1 = F.round(1)
sage: l = R1.gens()
sage: l[0]
k000^2 + k000

monomials()¶

Return an unordered list of monomials appearing in polynomials in this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: R1 = F.round(1)
sage: sorted(R1.monomials())
[k003, k002, k001, k000, k003^2, k002^2, k001^2, k000^2]

ngens()¶

Return number of polynomials in the system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: R0 = F.round(0)
sage: R0.ngens()
4

ring()¶

Return the polynomial ring the members of this system live in.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: R0 = F.round(0)
sage: print R0.ring().repr_long()
Polynomial Ring
 Base Ring : Finite Field of size 2
      Size : 20 Variables
  Block  0 : Ordering : degrevlex
             Names    : k100, k101, k102, k103, x100, x101, x102, x103, w100, w101, w102, w103, s000, s001, s002, s003
  Block  1 : Ordering : degrevlex
             Names    : k000, k001, k002, k003

subs(*args, **kwargs)¶

Substitute variables for every polynomial in this system and return a new system. See MPolynomial.subs for calling convention.

INPUT:

args - arguments to be passed to MPolynomial.subs
kwargs - keyword arguments to be passed to MPolynomial.subs

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: R1 = F.round(1)
sage: R1 = R1.subs(s) # the solution
sage: R1
(0, 0, 0, 0)

variables()¶

Return an unordered tuple of variables appearing in polynomials in this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: R1 = F.round(1)
sage: R1.variables()
(k000, k001, k002, k003)
sage: sorted(R1.variables())
[k003, k002, k001, k000]

sage.crypto.mq.mpolynomialsystem.MPolynomialSystem(arg1, arg2=None)¶

Construct a new polynomial system object.

INPUT:

arg1 - a multivariate polynomial ring or an ideal
arg2 - an iterable object of rounds, preferable MPolynomialRoundSystem, or polynomials (default:None)

EXAMPLES:

sage: P.<a,b,c,d> = PolynomialRing(GF(127),4)
sage: I = sage.rings.ideal.Katsura(P)

If a list of MPolynomialRoundSystems is provided, those form the rounds:

sage: mq.MPolynomialSystem(I.ring(), [mq.MPolynomialRoundSystem(I.ring(),I.gens())])
Polynomial System with 4 Polynomials in 4 Variables

If an ideal is provided, the generators are used:

sage: mq.MPolynomialSystem(I)
Polynomial System with 4 Polynomials in 4 Variables

If a list of polynomials is provided, the system has only one round:

sage: mq.MPolynomialSystem(I.ring(), I.gens())
Polynomial System with 4 Polynomials in 4 Variables

class sage.crypto.mq.mpolynomialsystem.MPolynomialSystem_generic(R, rounds)¶

Bases: sage.structure.sage_object.SageObject

coefficient_matrix(sparse=True)¶

Return tuple (A,v) where A is the coefficient matrix of this system and v the matching monomial vector.

Thus value of A[i,j] corresponds the coefficient of the monomial v[j] in the i-th polynomial in this system.

Monomials are order w.r.t. the term ordering of self.ring() in reverse order, i.e. such that the smallest entry comes last.

INPUT:

sparse - construct a sparse matrix (default: True)

EXAMPLE:

sage: P.<a,b,c,d> = PolynomialRing(GF(127),4)
sage: I = sage.rings.ideal.Katsura(P)
sage: I.gens()
(a + 2*b + 2*c + 2*d - 1, a^2 + 2*b^2 + 2*c^2 + 2*d^2 - a, 2*a*b + 2*b*c
+ 2*c*d - b, b^2 + 2*a*c + 2*b*d - c)

sage: F = mq.MPolynomialSystem(I)
sage: A,v = F.coefficient_matrix()
sage: A
[  0   0   0   0   0   0   0   0   0   1   2   2   2 126]
[  1   0   2   0   0   2   0   0   2 126   0   0   0   0]
[  0   2   0   0   2   0   0   2   0   0 126   0   0   0]
[  0   0   1   2   0   0   2   0   0   0   0 126   0   0]

sage: v
[a^2]
[a*b]
[b^2]
[a*c]
[b*c]
[c^2]
[b*d]
[c*d]
[d^2]
[  a]
[  b]
[  c]
[  d]
[  1]

sage: A*v
[        a + 2*b + 2*c + 2*d - 1]
[a^2 + 2*b^2 + 2*c^2 + 2*d^2 - a]
[      2*a*b + 2*b*c + 2*c*d - b]
[        b^2 + 2*a*c + 2*b*d - c]

connected_components()¶

Split the polynomial system in systems which do not share any variables.

EXAMPLE:

As an example consider one round of AES, which naturally splits into four subsystems which are independent:

sage: sr = mq.SR(2,4,4,8,gf2=True,polybori=True)
sage: F,s = sr.polynomial_system()
sage: Fz = mq.MPolynomialSystem(F.round(2))
sage: Fz.connected_components()
[Polynomial System with 128 Polynomials in 128 Variables,
 Polynomial System with 128 Polynomials in 128 Variables,
 Polynomial System with 128 Polynomials in 128 Variables,
 Polynomial System with 128 Polynomials in 128 Variables]

connection_graph()¶

Return the graph which has the variables of this system as vertices and edges between two variables if they appear in the same polynomial.

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing()
sage: F = mq.MPolynomialSystem([x*y + y + 1, z + 1])
sage: F.connection_graph()
Graph on 3 vertices

gen(ij)¶

Return an element in this system indexed by ij.

INPUT:

ij - tuple, slice, integer

EXAMPLES:

sage: P.<a,b,c,d> = PolynomialRing(GF(127),4)
sage: F = mq.MPolynomialSystem(sage.rings.ideal.Katsura(P))

ij-th polynomial overall:

sage: F[0] # indirect doctest
a + 2*b + 2*c + 2*d - 1

i-th to j-th polynomial overall:

sage: F[0:2]
(a + 2*b + 2*c + 2*d - 1, a^2 + 2*b^2 + 2*c^2 + 2*d^2 - a)

i-th round, j-th polynomial:

sage: F[0,1]
a^2 + 2*b^2 + 2*c^2 + 2*d^2 - a

gens()¶

Return tuple of polynomials in this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: l = F.gens()
sage: len(l), type(l)
(40, <type 'tuple'>)

groebner_basis(*args, **kwargs)¶

Compute and return a Groebner basis for the ideal spanned by the polynomials in this system (self.gens()).

INPUT:

args - list of arguments passed to

MPolynomialIdeal.groebner_basis call
kwargs - dictionary of arguments passed to

MPolynomialIdeal.groebner_basis call

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: gb = F.groebner_basis()
sage: Ideal(gb).basis_is_groebner()
True

ideal()¶

Return Sage ideal spanned by the elements of this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: P = F.ring()
sage: I = F.ideal()
sage: I.elimination_ideal(P('s000*s001*s002*s003*w100*w101*w102*w103*x100*x101*x102*x103'))
Ideal (k002 + (a^2)*k003 + 1, 
       k001 + (a^3)*k003 + (a + 1),
       k000 + (a^3 + a^2 + a)*k003 + (a^3 + a^2 + a), 
       k103 + (a^3)*k003 + (a^2 + 1), 
       k102 + (a^3 + a^2 + a)*k003 + (a^3 + 1), 
       k101 + k003 + (a^2 + a), 
       k100 + (a^2)*k003 + (a^2 + a), 
       k003^2 + (a^3 + a^2 + a)*k003 + (a^3 + a^2 + a)) 
of Multivariate Polynomial Ring in k100, k101, k102, k103,
x100, x101, x102, x103, w100, w101, w102, w103, s000,
s001, s002, s003, k000, k001, k002, k003 over Finite Field
in a of size 2^4

monomials()¶

Return an unordered tuple of monomials in this polynomial system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: len(F.monomials())
49

ngens()¶

Return number polynomials in this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: F.ngens()
56

nmonomials()¶

Return the number of monomials present in this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: F.nmonomials()
49

nrounds()¶

Return number of rounds of this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: F.nrounds()
4

nvariables()¶

Return number of variables present in this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: F.nvariables()
20

ring()¶

Return base ring.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True,gf2=True,order='block')
sage: F,s = sr.polynomial_system()
sage: print F.ring().repr_long()
Polynomial Ring
 Base Ring : Finite Field of size 2
      Size : 20 Variables
  Block  0 : Ordering : degrevlex
             Names    : k100, k101, k102, k103, x100, x101, x102, x103, w100, w101, w102, w103, s000, s001, s002, s003
  Block  1 : Ordering : degrevlex
             Names    : k000, k001, k002, k003

round(i)¶

Return i-th round of this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: R0 = F.round(1)
sage: R0
(k000^2 + k001, k001^2 + k002, k002^2 + k003, k003^2 + k000)

rounds()¶

Return a tuple of rounds of this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: l = F.rounds()
sage: len(l)
4

subs(*args, **kwargs)¶

Substitute variables for every polynomial in this system and return a new system. See MPolynomial.subs for calling convention.

INPUT:

args - arguments to be passed to MPolynomial.subs
kwargs - keyword arguments to be passed to MPolynomial.subs

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system(); F
Polynomial System with 40 Polynomials in 20 Variables
sage: F = F.subs(s); F
Polynomial System with 40 Polynomials in 16 Variables

variables()¶

Return all variables present in this system. This tuple may or may not be equal to the generators of the ring of this system.

EXAMPLE:

sage: sr = mq.SR(allow_zero_inversions=True)
sage: F,s = sr.polynomial_system()
sage: F.variables()[:10]
(k003, k002, k001, k000, s003, s002, s001, s000, w103, w102)

class sage.crypto.mq.mpolynomialsystem.MPolynomialSystem_gf2(R, rounds)¶

Bases: sage.crypto.mq.mpolynomialsystem.MPolynomialSystem_generic

Polynomial Systems over 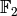$\mathbb{F}_2$ .

eliminate_linear_variables(maxlength=3, skip=<function <lambda> at 0x3e2a050>)¶

Return a new system where “linear variables” are eliminated.

In this function we call a variable “linear” if it appears as a leading term of a linear polynomial.

INPUT:

maxlength - an optional upper bound on the number of monomials by which a variable is replaced.
skip - an optional callable to skip eliminations. It must accept two parameters and return either True or False. The two parameters are the leading term and the tail of a polynomial (default: lambda lm,tail: False).

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing()
sage: F = mq.MPolynomialSystem([c + d + b + 1, a + c + d, a*b + c, b*c*d + c])
sage: F.eliminate_linear_variables().gens() # everything vanishes
()
sage: F.eliminate_linear_variables(maxlength=2).gens()
(b + c + d + 1, b*c + b*d + c, b*c*d + c)
sage: F.eliminate_linear_variables(skip=lambda lm,tail: str(lm)=='a').gens()
(a + c + d, a*c + a*d + a + c, c*d + c)

Note

This is called “massaging” in [CB07].

REFERENCES:

[CB07]

Nicolas T. Courtois, Gregory V. Bard Algebraic Cryptanalysis of the Data Encryption Standard; Cryptography and Coding – 11th IMA International Conference; 2007; available at http://eprint.iacr.org/2006/402

class sage.crypto.mq.mpolynomialsystem.MPolynomialSystem_gf2e(R, rounds)¶

Bases: sage.crypto.mq.mpolynomialsystem.MPolynomialSystem_generic

MPolynomialSystem over 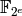$\mathbb{F}_{2^e}$ .

change_ring(k)¶

Project self onto k using the Weil restriction of scalars.

INPUT:

k - GF(2) (parameter only for compatible syntax)

EXAMPLE:

sage: k.<a> = GF(2^2)
sage: P.<x,y> = PolynomialRing(k,2)
sage: a = P.base_ring().gen()
sage: F = mq.MPolynomialSystem(P,[x*y + 1, a*x + 1])
sage: F
Polynomial System with 2 Polynomials in 2 Variables
sage: F2 = F.change_ring(GF(2)); F2
doctest... DeprecationWarning: The use of this function is deprecated please use the weil_restriction() function instead.
Polynomial System with 8 Polynomials in 4 Variables
sage: F2.gens()
(x1*y0 + x0*y1 + x1*y1,
x0*y0 + x1*y1 + 1,
x0 + x1,
x1 + 1,
x0^2 + x0,
x1^2 + x1,
y0^2 + y0,
y1^2 + y1)

Note

This function is deprecated use the weil_restriction() function instead.

weil_restriction()¶

Project this polynomial system to 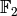$\mathbb{F}_2$ .

That is, compute the Weil restriction of scalars for the variety corresponding to this polynomial system and express it as a polynomial system over 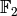$\mathbb{F}_2$ .

EXAMPLE:

sage: k.<a> = GF(2^2)
sage: P.<x,y> = PolynomialRing(k,2)
sage: a = P.base_ring().gen()
sage: F = mq.MPolynomialSystem(P,[x*y + 1, a*x + 1])
sage: F
Polynomial System with 2 Polynomials in 2 Variables
sage: F2 = F.weil_restriction(); F2
Polynomial System with 8 Polynomials in 4 Variables
sage: F2.gens()
(x1*y0 + x0*y1 + x1*y1,
x0*y0 + x1*y1 + 1,
x0 + x1,
x1 + 1,
x0^2 + x0,
x1^2 + x1,
y0^2 + y0,
y1^2 + y1)

Another bigger example for a small scale AES:

sage: sr = mq.SR(1,1,1,4,gf2=False)
sage: F,s = sr.polynomial_system(); F
Polynomial System with 40 Polynomials in 20 Variables
sage: F2 = F.weil_restriction(); F2
Polynomial System with 240 Polynomials in 80 Variables

sage.crypto.mq.mpolynomialsystem.is_MPolynomialRoundSystem(F)¶

Return True if F is an MPolynomialRoundSystem.

INPUT:

F - anything

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQ)
sage: I = [[x^2 + y^2], [x^2 - y^2]]
sage: F = mq.MPolynomialSystem(P,I); F
Polynomial System with 2 Polynomials in 2 Variables
sage: mq.is_MPolynomialRoundSystem(F.round(0))
True

sage.crypto.mq.mpolynomialsystem.is_MPolynomialSystem(F)¶

Return True if F is an MPolynomialSystem.

INPUT:

- ``F`` - anything

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQ)
sage: I = [[x^2 + y^2], [x^2 - y^2]]
sage: F = mq.MPolynomialSystem(P,I); F
Polynomial System with 2 Polynomials in 2 Variables
sage: mq.is_MPolynomialSystem(F)
True

Multivariate Polynomial Systems.¶

Previous topic

Next topic

This Page

Navigation

Multivariate Polynomial Systems.¶

Previous topic

Next topic

This Page

Quick search

Navigation