Word paths

This module implements word paths, which is an application of Combinatorics on Words to Discrete Geometry. A word path is the representation of a word as a discrete path in a vector space using a one-to-one correspondence between the alphabet and a set of vectors called steps. Many problems surrounding 2d lattice polygons (such as questions of self-intersection, area, inertia moment, etc.) can be solved in linear time (linear in the length of the perimeter) using theory from Combinatorics on Words.

On the square grid, the encoding of a path using a four-letter alphabet (for East, North, West and South directions) is also known as the Freeman chain code [1,2] (see [3] for further reading).

AUTHORS:

• Arnaud Bergeron (2008) : Initial version, path on the square grid
• Sebastien Labbe (2009-01-14) : New classes and hierarchy, doc and functions.

EXAMPLES:

The combinatorial class of all paths defined over three given steps:

sage: P = WordPaths('abc', steps=[(1,2), (-3,4), (0,-3)]); P
Word Paths over 3 steps

This defines a one-to-one correspondence between alphabet and steps:

sage: d = P.letters_to_steps()
sage: sorted(d.items())
[('a', (1, 2)), ('b', (-3, 4)), ('c', (0, -3))]

Creation of a path from the combinatorial class P defined above:

sage: p = P('abaccba'); p 
Path: abaccba

Many functions can be used on p: the coordinates of its trajectory, ask whether p is a closed path, plot it and many other:

sage: list(p.points())  
[(0, 0), (1, 2), (-2, 6), (-1, 8), (-1, 5), (-1, 2), (-4, 6), (-3, 8)] 
sage: p.is_closed()
False
sage: p.plot()

To obtain a list of all the available word path specific functions, use help(p):

sage: help(p)
Help on FiniteWordPath_2d_str in module sage.combinat.words.paths object: 
...
Methods inherited from FiniteWordPath_2d:
...
Methods inherited from FiniteWordPath_all:
...
This only works on Python classes that derive from SageObject.

Since p is a finite word, many functions from the word library are available:

sage: p.crochemore_factorization()
(a, b, a, c, c, ba)
sage: p.is_palindrome()
False
sage: p[:3]
Path: aba
sage: len(p)
7

P also herits many functions from Words:

sage: P = WordPaths('rs', steps=[(1,2), (-1,4)]); P
Word Paths over 2 steps
sage: P.alphabet()
Ordered Alphabet ['r', 's']
sage: list(P.iterate_by_length(3))                 
[Path: rrr,
 Path: rrs,
 Path: rsr,
 Path: rss,
 Path: srr,
 Path: srs,
 Path: ssr,
 Path: sss]

When the number of given steps is half the size of alphabet, the opposite of vectors are used:

sage: P = WordPaths('abcd', [(1,0), (0,1)])
sage: sorted(P.letters_to_steps().items())
[('a', (1, 0)), ('b', (0, 1)), ('c', (-1, 0)), ('d', (0, -1))]

Some built-in combinatorial classes of paths:

sage: P = WordPaths('abAB', steps='square_grid'); P
Word Paths on the square grid

sage: D = WordPaths('()', steps='dyck'); D
Finite Dyck paths
sage: d = D('()()()(())'); d
Path: ()()()(())
sage: d.plot()

sage: P = WordPaths('abcdef', steps='triangle_grid')
sage: p = P('babaddefadabcadefaadfafabacdefa')
sage: p.plot()

Vector steps may be in more than 2 dimensions:

sage: d = [(1,0,0), (0,1,0), (0,0,1)]
sage: P = WordPaths(alphabet='abc', steps=d); P
Word Paths over 3 steps
sage: p = P('abcabcabcabcaabacabcababcacbabacacabcaccbcac')
sage: p.plot()

sage: d = [(1,3,5,1), (-5,1,-6,0), (0,0,1,9), (4,2,-1,0)]
sage: P = WordPaths(alphabet='rstu', steps=d); P
Word Paths over 4 steps
sage: p = P('rtusuusususuturrsust'); p
Path: rtusuusususuturrsust
sage: p.end_point()
(5, 31, -26, 30)

sage: CubePaths = WordPaths('abcABC', steps='cube_grid'); CubePaths
Word Paths on the cube grid
sage: CubePaths('abcabaabcabAAAAA').plot() 

The input data may be a str, a list, a tuple, a callable or a finite iterator:

sage: P = WordPaths([0, 1, 2, 3])
sage: P([0,1,2,3,2,1,2,3,2])
Path: 012321232
sage: P((0,1,2,3,2,1,2,3,2))
Path: 012321232
sage: P(lambda n:n%4, length=10)
Path: 0123012301
sage: P(iter([0,3,2,1]), length='finite')
Path: 0321 

REFERENCES:

• [1] Freeman, H.: On the encoding of arbitrary geometric configurations. IRE Trans. Electronic Computer 10 (1961) 260-268.
• [2] Freeman, H.: Boundary encoding and processing. In Lipkin, B., Rosenfeld, A., eds.: Picture Processing and Psychopictorics, Academic Press, New York (1970) 241-266.
• [3] Braquelaire, J.P., Vialard, A.: Euclidean paths: A new representation of boundary of discrete regions. Graphical Models and Image Processing 61 (1999) 16-43.
• [4] http://en.wikipedia.org/wiki/Regular_tiling
• [5] http://en.wikipedia.org/wiki/Dyck_word

class sage.combinat.words.paths.FiniteWordPath_2d

Bases: sage.combinat.words.paths.FiniteWordPath_all

animate()

Returns an animation object illustrating the path growing step by step.

EXAMPLES:

sage: P = WordPaths('abAB')
sage: p = P('aaababbb')
sage: a = p.animate(); a
Animation with 9 frames
sage: show(a)       # optional -- requires convert command
sage: a.gif(delay=35, iterations=3)       # optional

sage: P = WordPaths('abcdef',steps='triangle')
sage: p =  P('abcdef')
sage: p.animate()
Animation with 8 frames

If the path is closed, the plain polygon is added at the end of the animation:

sage: P = WordPaths('abAB')
sage: p = P('ababAbABABaB')
sage: a = p.animate(); a
Animation with 14 frames

Another example illustrating a Fibonacci tile:

sage: w = words.fibonacci_tile(2) 
sage: show(w.animate())      # optional

The first 4 Fibonacci tiles in an animation:

sage: a = words.fibonacci_tile(0).animate()
sage: b = words.fibonacci_tile(1).animate()
sage: c = words.fibonacci_tile(2).animate()
sage: d = words.fibonacci_tile(3).animate()
sage: (a*b*c*d).show()       # optional

Note

If ImageMagick is not installed, you will get an error message like this:

/usr/local/share/sage/local/bin/sage-native-execute: 8: convert:
not found

Error: ImageMagick does not appear to be installed. Saving an
animation to a GIF file or displaying an animation requires
ImageMagick, so please install it and try again.

See www.imagemagick.org, for example.

area()

Returns the area of a closed path.

INPUT:

• self - a closed path

EXAMPLES:

sage: P = WordPaths('abcd',steps=[(1,1),(-1,1),(-1,-1),(1,-1)])
sage: p = P('abcd')
sage: p.area()          #todo: not implemented
2

directive_vector(options={'rgbcolor': 'blue'})

Returns an arrow 2d graphics that goes from the start of the path to the end.

INPUT:

• options - (dictionary, default: {‘rgbcolor’: ‘blue’} graphic options for the arrow

EXAMPLES:

sage: P = WordPaths('abcd'); P
Word Paths on the square grid
sage: p = P('aaaccaccacacacaccccccbbdd'); p
Path: aaaccaccacacacaccccccbbdd
sage: R = p.plot() + p.directive_vector()  
sage: show(R, axes=False, aspect_ratio=1)

TESTS:

A closed path:

sage: P('acbd').directive_vector()                     

height()

Returns the height of self.

The height of a 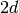-path is merely the difference between the highest and the lowest -coordinate of each points traced by it.

OUTPUT:

non negative real number

EXAMPLES:

sage: Freeman = WordPaths('abAB')
sage: Freeman('aababaabbbAA').height()
5

The function is well-defined if self is not simple or close:

sage: Freeman('aabAAB').height()
1
sage: Freeman('abbABa').height()
2

This works for any 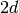-paths:

sage: Paths = WordPaths('ab', steps=[(1,0),(1,1)])
sage: p = Paths('abbaa')
sage: p.height()
2
sage: DyckPaths = WordPaths('ab', steps='dyck')
sage: p = DyckPaths('abaabb')
sage: p.height()
2
sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.height()
2.59807621135332

plot(pathoptions={'rgbcolor': 'red', 'thickness': 3}, fill=True, filloptions={'alpha': 0.20000000000000001, 'rgbcolor': 'red'}, startpoint=True, startoptions={'pointsize': 100, 'rgbcolor': 'red'}, endarrow=True, arrowoptions={'width': 3, 'rgbcolor': 'red', 'arrowsize': 20}, gridlines=False, gridoptions={})

Returns a 2d Graphics illustrating the path.

INPUT:

• pathoptions - (dict, default:dict(rgbcolor=’red’,thickness=3)), options for the path drawing
• fill - (boolean, default: True), if fill is True and if the path is closed, the inside is colored
• filloptions - (dict, default:dict(rgbcolor=’red’,alpha=0.2)), ptions for the inside filling
• startpoint - (boolean, default: True), draw the start point?
• startoptions - (dict, default:dict(rgbcolor=’red’,pointsize=100)) options for the start point drawing
• endarrow - (boolean, default: True), draw an arrow end at the end?
• arrowoptions - (dict, default:dict(rgbcolor=’red’,arrowsize=20, width=3)) options for the end point arrow
• gridlines- (boolean, default: False), show gridlines?
• gridoptions - (dict, default: {}), options for the gridlines

EXAMPLES:

A non closed path on the square grid:

sage: P = WordPaths('abAB')
sage: P('abababAABAB').plot()

A closed path on the square grid:

sage: P('abababAABABB').plot()

A dyck path:

sage: P = WordPaths('()', steps='dyck')
sage: P('()()()((()))').plot()        

A path in the triangle grid:

sage: P = WordPaths('abcdef', steps='triangle_grid')
sage: P('abcdedededefab').plot()

A polygon of length 220 that tiles the plane in two ways:

sage: P = WordPaths('abAB')
sage: P('aBababAbabaBaBABaBabaBaBABAbABABaBabaBaBABaBababAbabaBaBABaBabaBaBABAbABABaBABAbAbabAbABABaBABAbABABaBabaBaBABAbABABaBABAbAbabAbABAbAbabaBababAbABAbAbabAbABABaBABAbAbabAbABAbAbabaBababAbabaBaBABaBababAbabaBababAbABAbAbab').plot()

With gridlines:

sage: P('ababababab').plot(gridlines=True)

TESTS:

sage: P = WordPaths('abAB')
sage: P().plot()     
sage: sum(map(plot,map(P,['a','A','b','B'])))

width()

Returns the width of self.

The height of a 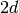-path is merely the difference between the rightmost and the leftmost -coordinate of each points traced by it.

OUTPUT:

non negative real number

EXAMPLES:

sage: Freeman = WordPaths('abAB')
sage: Freeman('aababaabbbAA').width()
5

The function is well-defined if self is not simple or close:

sage: Freeman('aabAAB').width()
2
sage: Freeman('abbABa').width()
1

This works for any 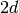-paths:

sage: Paths = WordPaths('ab', steps=[(1,0),(1,1)])
sage: p = Paths('abbaa')
sage: p.width()
5
sage: DyckPaths = WordPaths('ab', steps='dyck')
sage: p = DyckPaths('abaabb')
sage: p.width()
6
sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.width()
4.50000000000000

xmax()

Returns the maximum of the x-coordinates of the path.

EXAMPLES:

sage: P = WordPaths('0123')
sage: p = P('0101013332')
sage: p.xmax()
3

This works for any 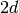-paths:

sage: Paths = WordPaths('ab', steps=[(1,-1),(-1,1)])
sage: p = Paths('ababa')
sage: p.xmax()
1
sage: DyckPaths = WordPaths('ab', steps='dyck')
sage: p = DyckPaths('abaabb')
sage: p.xmax()
6
sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.xmax()
4.50000000000000

xmin()

Returns the minimum of the x-coordinates of the path.

EXAMPLES:

sage: P = WordPaths('0123')
sage: p = P('0101013332')
sage: p.xmin()
0

This works for any 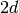-paths:

sage: Paths = WordPaths('ab', steps=[(1,0),(-1,1)])
sage: p = Paths('abbba')
sage: p.xmin()
-2
sage: DyckPaths = WordPaths('ab', steps='dyck')
sage: p = DyckPaths('abaabb')
sage: p.xmin()
0
sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.xmin()
0.000000000000000

ymax()

Returns the maximum of the y-coordinates of the path.

EXAMPLES:

sage: P = WordPaths('0123')
sage: p = P('0101013332')
sage: p.ymax()
3

This works for any 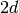-paths:

sage: Paths = WordPaths('ab', steps=[(1,-1),(-1,1)])
sage: p = Paths('ababa')
sage: p.ymax()
0 
sage: DyckPaths = WordPaths('ab', steps='dyck')
sage: p = DyckPaths('abaabb')
sage: p.ymax()
2
sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.ymax()
2.59807621135332

ymin()

Returns the minimum of the y-coordinates of the path.

EXAMPLES:

sage: P = WordPaths('0123')
sage: p = P('0101013332')
sage: p.ymin()
0

This works for any 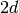-paths:

sage: Paths = WordPaths('ab', steps=[(1,-1),(-1,1)])
sage: p = Paths('ababa')
sage: p.ymin()
-1
sage: DyckPaths = WordPaths('ab', steps='dyck')
sage: p = DyckPaths('abaabb')
sage: p.ymin()
0
sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.ymin()
0.000000000000000

class sage.combinat.words.paths.FiniteWordPath_2d_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_2d_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_2d_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_2d_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_2d_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2),(3,4)])
sage: p = P(['a','b','a']);p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_2d_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_2d_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2),(3,4)])
sage: p = P('aba'); p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_2d_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_2d_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_2d, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2),(3,4)])
sage: p = P(('a','b','a'));p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_2d_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_3d

Bases: sage.combinat.words.paths.FiniteWordPath_all

plot(pathoptions={'arrow_head': True, 'rgbcolor': 'red', 'thickness': 3}, startpoint=True, startoptions={'rgbcolor': 'red', 'size': 10})

INPUT:

• pathoptions - (dict, default:dict(rgbcolor=’red’,arrow_head=True, thickness=3)), options for the path drawing

• startpoint - (boolean, default: True), draw the start point?

• startoptions - (dict, default:dict(rgbcolor=’red’,size=10))

  options for the start point drawing

EXAMPLES:

sage: d = ( vector((1,3,2)), vector((2,-4,5)) )
sage: P = WordPaths(alphabet='ab', steps=d); P
Word Paths over 2 steps
sage: p = P('ababab'); p
Path: ababab
sage: p.plot()

sage: P = WordPaths('abcABC', steps='cube_grid')      
sage: p = P('abcabcAABBC')
sage: p.plot()

class sage.combinat.words.paths.FiniteWordPath_3d_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_3d_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_3d_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_3d_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_3d_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2,0),(3,4,0)])
sage: p = P(['a','b','a']);p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_3d_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_3d_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2,0),(3,4,0)])
sage: p = P('aba'); p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_3d_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_3d_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_3d, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2,0),(3,4,0)])
sage: p = P(('a','b','a'));p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_3d_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_all

Bases: sage.structure.sage_object.SageObject

end_point(*args, **kwds)

Returns the end point of the path.

EXAMPLES:

sage: WordPaths('abcdef')('abababab').end_point()
(6, 2*sqrt3)
sage: WordPaths('abAB')('abababab').end_point()
(4, 4)
sage: P = WordPaths('abcABC', steps='cube_grid')
sage: P('ababababCC').end_point()
(4, 4, -2)
sage: WordPaths('abcdef')('abcdef').end_point() 
(0, 0)
sage: P = WordPaths('abc', steps=[(1,3,7,9),(-4,1,0,0),(0,32,1,8)])
sage: P('abcabababacaacccbbcac').end_point()
(-16, 254, 63, 128)

is_closed()

Returns True if the path is closed, i.e. if the origin and the end of the path are equal.

EXAMPLES:

sage: P = WordPaths('abcd', steps=[(1,0),(0,1),(-1,0),(0,-1)])
sage: P('abcd').is_closed()
True
sage: P('abc').is_closed() 
False
sage: P().is_closed()     
True
sage: P('aacacc').is_closed() 
True

is_simple()

Returns True if the path is simple, i.e. if all its points are distincts.

If the path is closed, the last point is not considered.

EXAMPLES:

sage: P = WordPaths('abcdef',steps='triangle_grid');P
Word Paths on the triangle grid
sage: P('abc').is_simple()
True
sage: P('abcde').is_simple()
True
sage: P('abcdef').is_simple()
True
sage: P('ad').is_simple()    
True
sage: P('aabdee').is_simple()
False

points(include_last=True)

Returns an iterator yielding a list of points used to draw the path represented by this word.

INPUT:

• include_last - bool (default: True) whether to include the last point

EXAMPLES:

A simple closed square:

sage: P = WordPaths('abAB')
sage: list(P('abAB').points())
[(0, 0), (1, 0), (1, 1), (0, 1), (0, 0)]

A simple closed square without the last point:

sage: list(P('abAB').points(include_last=False))
[(0, 0), (1, 0), (1, 1), (0, 1)]

sage: list(P('abaB').points())
[(0, 0), (1, 0), (1, 1), (2, 1), (2, 0)]

start_point()

Return the starting point of self.

OUTPUT:

vector

EXAMPLES:

sage: WordPaths('abcdef')('abcdef').start_point()
(0, 0)
sage: WordPaths('abcdef', steps='cube_grid')('abcdef').start_point()
(0, 0, 0)
sage: P = WordPaths('ab', steps=[(1,0,0,0),(0,1,0,0)])
sage: P('abbba').start_point()
(0, 0, 0, 0)

tikz_trajectory()

Returns the trajectory of self as a tikz str.

EXAMPLES:

sage: P = WordPaths('abcdef')
sage: p = P('abcde')
sage: p.tikz_trajectory()
'(0.000, 0.000) -- (1.00, 0.000) -- (1.50, 0.866) -- (1.00, 1.73) -- (0.000, 1.73) -- (-0.500, 0.866)'

class sage.combinat.words.paths.FiniteWordPath_all_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_all_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_all_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_all_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_all_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths(['a','b'],[(1,2,0,0),(3,4,0,0)])
sage: p = P(['a','b','a']);p
Path: aba
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_all_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_all_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab',[(1,2,0,0),(3,4,0,0)])
sage: p = P('aabbb'); p
Path: aabbb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_all_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_all_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_all, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab',[(1,2,0,0),(3,4,0,0)])
sage: p = P( ('a','b','b') ); p
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_all_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_cube_grid

Bases: sage.combinat.words.paths.FiniteWordPath_3d

class sage.combinat.words.paths.FiniteWordPath_cube_grid_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_cube_grid_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_cube_grid_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_cube_grid_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_cube_grid_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='cube')
sage: p = P(['a','b','b']); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_cube_grid_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_cube_grid_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='cube')
sage: p = P('abb'); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_cube_grid_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_cube_grid_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_cube_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='cube')
sage: p = P(('a','b','b')); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_cube_grid_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_dyck

Bases: sage.combinat.words.paths.FiniteWordPath_2d

class sage.combinat.words.paths.FiniteWordPath_dyck_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_dyck_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_dyck_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_dyck_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_dyck_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab', steps='dyck')
sage: p = P(['a','b','b']); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_dyck_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_dyck_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab', steps='dyck')
sage: p = P('abb'); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_dyck_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_dyck_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_dyck, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab', steps='dyck')
sage: p = P(('a','b','b')); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_dyck_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid(parent, *args, **kwds)

Bases: sage.combinat.words.paths.FiniteWordPath_triangle_grid

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='hexagon')
sage: p = P(['a','b','b']); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='hexagon')
sage: p = P('abb'); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_hexagonal_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='hexagon')
sage: p = P(('a','b','b')); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_hexagonal_grid_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_north_east

Bases: sage.combinat.words.paths.FiniteWordPath_2d

class sage.combinat.words.paths.FiniteWordPath_north_east_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_north_east_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_north_east_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_north_east_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_north_east_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab', steps='ne')
sage: p = P(['a','b','b']); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_north_east_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_north_east_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab', steps='ne')
sage: p = P('abb'); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_north_east_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_north_east_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_north_east, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('ab', steps='ne')
sage: p = P(('a','b','b')); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_north_east_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_square_grid

Bases: sage.combinat.words.paths.FiniteWordPath_2d

area()

Returns the area of a closed path.

INPUT:

• self - a closed path

EXAMPLES:

sage: P = WordPaths('abAB', steps='square_grid')  
sage: P('abAB').area()
1
sage: P('aabbAABB').area()
4
sage: P('aabbABAB').area()
3

The area of the Fibonacci tiles:

sage: [words.fibonacci_tile(i).area() for i in range(6)]
[1, 5, 29, 169, 985, 5741]
sage: [words.dual_fibonacci_tile(i).area() for i in range(6)]
[1, 5, 29, 169, 985, 5741]
sage: sloane_find(_, nresults=1) #optional - internet
Searching Sloane's online database...
[[1653,
  'Numbers n such that 2*n^2 - 1 is a square.',
  [1,
   5,
   29,
   169,
   985,
   5741,
   33461,
   195025,
   1136689,
   6625109,
   38613965,
   225058681,
   1311738121,
   7645370045,
   44560482149,
   259717522849,
   1513744654945,
   8822750406821,
   51422757785981,
   299713796309065,
   1746860020068409]]]

TESTS:

sage: P = WordPaths('abAB', steps='square_grid')  
sage: P('a').area()    
...
TypeError: the path must be closed to compute its area

is_closed()

Returns True if self represents a closed path and False otherwise.

EXAMPLES:

sage: P = WordPaths('abAB', steps='square_grid')
sage: P('aA').is_closed()
True
sage: P('abAB').is_closed()
True
sage: P('ababAABB').is_closed()
True
sage: P('aaabbbAABB').is_closed()
False
sage: P('ab').is_closed()  
False

is_simple()

Returns True if the path is simple, i.e. if all its points are distincts.

If the path is closed, the last point is not considered.

Note

The linear algorithm described in the thesis of Xavier Provençal should be implemented here.

EXAMPLES:

sage: P = WordPaths('abAB', steps='square_grid')  
sage: P('abab').is_simple()
True
sage: P('abAB').is_simple()    
True
sage: P('abA').is_simple() 
True
sage: P('aabABB').is_simple()
False
sage: P().is_simple()        
True
sage: P('A').is_simple()
True
sage: P('aA').is_simple()
True
sage: P('aaA').is_simple()
False

REFERENCES:

• Provençal, X., Combinatoires des mots, geometrie discrete et pavages, These de doctorat en Mathematiques, Montreal, UQAM, septembre 2008, 115 pages.

tikz_trajectory()

Returns the trajectory of self as a tikz str.

EXAMPLES:

sage: f = words.fibonacci_tile(1)
sage: f.tikz_trajectory()
'(0, 0) -- (0, -1) -- (-1, -1) -- (-1, -2) -- (0, -2) -- (0, -3) -- (1, -3) -- (1, -2) -- (2, -2) -- (2, -1) -- (1, -1) -- (1, 0) -- (0, 0)'

class sage.combinat.words.paths.FiniteWordPath_square_grid_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_square_grid_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_square_grid_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_square_grid_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_square_grid_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcd', steps='square')
sage: p = P(['a','b','b']); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_square_grid_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_square_grid_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcd', steps='square')
sage: p = P('abccc'); p 
Path: abccc
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_square_grid_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_square_grid_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_square_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcd', steps='square')
sage: p = P(('a','b','b')); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_square_grid_tuple'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_triangle_grid

Bases: sage.combinat.words.paths.FiniteWordPath_2d

xmax()

Returns the maximum of the x-coordinates of the path.

EXAMPLES:

sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.xmax()
4.50000000000000
sage: w = WordPaths('abcABC', steps='triangle')('ABAcacacababababcbcbAC')
sage: w.xmax()
4.00000000000000

xmin()

Returns the minimum of the x-coordinates of the path.

EXAMPLES:

sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.xmin()
0.000000000000000
sage: w = WordPaths('abcABC', steps='triangle')('ABAcacacababababcbcbAC')
sage: w.xmin()
-3.00000000000000

ymax()

Returns the maximum of the y-coordinates of the path.

EXAMPLES:

sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.ymax()
2.59807621135332
sage: w = WordPaths('abcABC', steps='triangle')('ABAcacacababababcbcbAC')
sage: w.ymax()
8.66025403784439

ymin()

Returns the minimum of the y-coordinates of the path.

EXAMPLES:

sage: w = WordPaths('abcABC', steps='triangle')('ababcaaBC')
sage: w.ymin()
0.000000000000000
sage: w = WordPaths('abcABC', steps='triangle')('ABAcacacababababcbcbAC')
sage: w.ymin()
-0.866025403784439

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_callable(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_callable_with_caching(parent, callable, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_callable_with_caching, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_iter(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_iter_with_caching(parent, iter, length=None)

Bases: sage.combinat.words.word_infinite_datatypes.WordDatatype_iter_with_caching, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_list

Bases: sage.combinat.words.word_datatypes.WordDatatype_list, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='triangle')
sage: p = P(['a','b','b']); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_triangle_grid_list'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_str

Bases: sage.combinat.words.word_datatypes.WordDatatype_str, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='triangle')
sage: p = P('abb'); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_triangle_grid_str'>
sage: p == loads(dumps(p))
True

class sage.combinat.words.paths.FiniteWordPath_triangle_grid_tuple

Bases: sage.combinat.words.word_datatypes.WordDatatype_tuple, sage.combinat.words.paths.FiniteWordPath_triangle_grid, sage.combinat.words.finite_word.FiniteWord_class

TESTS:

sage: P = WordPaths('abcdef', steps='triangle')
sage: p = P(('a','b','b')); p 
Path: abb
sage: type(p)
<class 'sage.combinat.words.paths.FiniteWordPath_triangle_grid_tuple'>
sage: p == loads(dumps(p))
True

sage.combinat.words.paths.WordPaths(alphabet, steps=None)

Returns the combinatorial class of paths of the given type of steps.

INPUT:

• alphabet - ordered alphabet
• steps - (default is None). It can be one of the following:
  • an iterable ordered container of as many vectors as there are letters in the alphabet. The vectors are associated to the letters according to their order in steps. The vectors can be a tuple or anything that can be passed to vector function.
  • an iterable ordered container of k vectors where k is half the size of alphabet. The vectors and their opposites are associated to the letters according to their order in steps (given vectors first, opposite vectors after).
  • None: In this case, the type of steps are guessed from the length of alphabet.
  • ‘square_grid’ or ‘square’ : (default when size of alphabet is 4) The order is : East, North, West, South.
  • ‘triangle_grid’ or ‘triangle’:
  • ‘hexagonal_grid’ or ‘hexagon’ :(default when size of alphabet is 6)
  • ‘cube_grid’ or ‘cube’ :
  • ‘north_east’, ‘ne’ or ‘NE’ : (the default when size of alphabet is 2)
  • ‘dyck’:

OUTPUT:

• The combinatorial class of all paths of the given type.

EXAMPLES:

The steps can be given explicitely:

sage: WordPaths('abc', steps=[(1,2), (-1,4), (0,-3)])
Word Paths over 3 steps

Different type of input alphabet:

sage: WordPaths(range(3), steps=[(1,2), (-1,4), (0,-3)])
Word Paths over 3 steps
sage: WordPaths(['cric','crac','croc'], steps=[(1,2), (1,4), (0,3)])
Word Paths over 3 steps

Directions can be in three dimensions as well:

sage: WordPaths('ab', steps=[(1,2,2),(-1,4,2)])
Word Paths over 2 steps

When the number of given steps is half the size of alphabet, the opposite of vectors are used:

sage: P = WordPaths('abcd', [(1,0), (0,1)])
sage: P
Word Paths over 4 steps
sage: sorted(P.letters_to_steps().items())
[('a', (1, 0)), ('b', (0, 1)), ('c', (-1, 0)), ('d', (0, -1))]

When no steps are given, default classes are returned:

sage: WordPaths('ab')                      
Word Paths in North and East steps
sage: WordPaths(range(4))
Word Paths on the square grid
sage: WordPaths(range(6))
Word Paths on the hexagonal grid

There are many type of built-in steps...

On a two letters alphabet:

sage: WordPaths('ab', steps='north_east')
Word Paths in North and East steps
sage: WordPaths('()', steps='dyck')
Finite Dyck paths

On a four letters alphabet:

sage: WordPaths('ruld', steps='square_grid')
Word Paths on the square grid

On a six letters alphabet:

sage: WordPaths('abcdef', steps='hexagonal_grid')
Word Paths on the hexagonal grid
sage: WordPaths('abcdef', steps='triangle_grid')
Word Paths on the triangle grid
sage: WordPaths('abcdef', steps='cube_grid')
Word Paths on the cube grid

TESTS:

sage: WordPaths(range(5))
...
TypeError: Unable to make a class WordPaths from Ordered Alphabet [0, 1, 2, 3, 4]
sage: WordPaths('abAB', steps='square_gridd')
...
TypeError: Unknown type of steps : square_gridd

class sage.combinat.words.paths.WordPaths_all(alphabet, steps)

Bases: sage.combinat.words.words.Words_over_OrderedAlphabet

The combinatorial class of all paths, i.e of all words over an alphabet where each letter is mapped to a step (a vector).

letters_to_steps()

Returns the dictionary mapping letters to vectors (steps).

EXAMPLES:

sage: d = WordPaths('ab').letters_to_steps()
sage: sorted(d.items())
[('a', (0, 1)), ('b', (1, 0))]
sage: d = WordPaths('abcd').letters_to_steps()
sage: sorted(d.items()) 
[('a', (1, 0)), ('b', (0, 1)), ('c', (-1, 0)), ('d', (0, -1))]
sage: d = WordPaths('abcdef').letters_to_steps()
sage: sorted(d.items())
[('a', (1, 0)), 
 ('b', (1/2, 1/2*sqrt3)), 
 ('c', (-1/2, 1/2*sqrt3)), 
 ('d', (-1, 0)), 
 ('e', (-1/2, -1/2*sqrt3)), 
 ('f', (1/2, -1/2*sqrt3))]

vector_space()

Return the vector space over which the steps of the paths are defined.

EXAMPLES:

sage: WordPaths('ab',steps='dyck').vector_space()
Ambient free module of rank 2 over the principal ideal domain Integer Ring
sage: WordPaths('ab',steps='north_east').vector_space()
Ambient free module of rank 2 over the principal ideal domain Integer Ring
sage: WordPaths('abcd',steps='square_grid').vector_space()
Ambient free module of rank 2 over the principal ideal domain Integer Ring
sage: WordPaths('abcdef',steps='hexagonal_grid').vector_space()
Vector space of dimension 2 over Number Field in sqrt3 with defining polynomial x^2 - 3
sage: WordPaths('abcdef',steps='cube_grid').vector_space()     
Ambient free module of rank 3 over the principal ideal domain Integer Ring
sage: WordPaths('abcdef',steps='triangle_grid').vector_space()
Vector space of dimension 2 over Number Field in sqrt3 with defining polynomial x^2 - 3

class sage.combinat.words.paths.WordPaths_cube_grid(alphabet)

Bases: sage.combinat.words.paths.WordPaths_all

The combinatorial class of all paths on the cube grid.

class sage.combinat.words.paths.WordPaths_dyck(alphabet)

Bases: sage.combinat.words.paths.WordPaths_all

The combinatorial class of all dyck paths.

class sage.combinat.words.paths.WordPaths_hexagonal_grid(alphabet)

Bases: sage.combinat.words.paths.WordPaths_triangle_grid

The combinatorial class of all paths on the hexagonal grid.

class sage.combinat.words.paths.WordPaths_north_east(alphabet)

Bases: sage.combinat.words.paths.WordPaths_all

The combinatorial class of all paths using North and East directions.

class sage.combinat.words.paths.WordPaths_square_grid(alphabet)

Bases: sage.combinat.words.paths.WordPaths_all

The combinatorial class of all paths on the square grid.

class sage.combinat.words.paths.WordPaths_triangle_grid(alphabet)

Bases: sage.combinat.words.paths.WordPaths_all

The combinatorial class of all paths on the triangle grid.