Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Words »

AUTHORS:
EXAMPLES:
Finite words from python strings, lists and tuples:
sage: Word("abbabaab")
word: abbabaab
sage: Word([0, 1, 1, 0, 1, 0, 0, 1])
word: 01101001
sage: Word( ('a', 0, 5, 7, 'b', 9, 8) )
word: a057b98
Finite words from functions:
sage: f = lambda n : n%3
sage: Word(f, length=13)
word: 0120120120120
Finite words from iterators:
sage: from itertools import count
sage: Word(count(), length=10)
word: 0123456789
sage: Word( iter('abbccdef') )
word: abbccdef
Finite words from words via concatenation:
sage: u = Word("abcccabba")
sage: v = Word([0, 4, 8, 8, 3])
sage: u * v
word: abcccabba04883
sage: v * u
word: 04883abcccabba
sage: u + v
word: abcccabba04883
sage: u^3 * v^(8/5)
word: abcccabbaabcccabbaabcccabba04883048
Finite words from infinite words:
sage: vv = v^Infinity
sage: vv[10000:10015]
word: 048830488304883
Finite words in a specific combinatorial class:
sage: W = Words("ab")
sage: W
Words over Ordered Alphabet ['a', 'b']
sage: W("abbabaab")
word: abbabaab
sage: W(["a","b","b","a","b","a","a","b"])
word: abbabaab
sage: W( iter('ababab') )
word: ababab
Finite word as the image under a morphism:
sage: m = WordMorphism({0:[4,4,5,0],5:[0,5,5],4:[4,0,0,0]})
sage: m(0)
word: 4450
sage: m(0, order=2)
word: 400040000554450
sage: m(0, order=3)
word: 4000445044504450400044504450445044500550...
There are more than 100 functions defined on a finite word. Here are some of them:
sage: w = Word('abaabbba'); w
word: abaabbba
sage: w.is_palindrome()
False
sage: w.is_lyndon()
False
sage: w.number_of_factors()
28
sage: w.critical_exponent()
3
sage: print w.lyndon_factorization()
(ab, aabbb, a)
sage: print w.crochemore_factorization()
(a, b, a, ab, bb, a)
sage: st = w.suffix_tree()
sage: st
Implicit Suffix Tree of the word: abaabbba
sage: st.show(word_labels=True)
sage: T = words.FibonacciWord('ab')
sage: T.longest_common_prefix(Word('abaabababbbbbb'))
word: abaababa
As matrix and many other sage objects, words have a parent:
sage: u = Word('xyxxyxyyy')
sage: u.parent()
Words
sage: v = Word('xyxxyxyyy', alphabet='xy')
sage: v.parent()
Words over Ordered Alphabet ['x', 'y']
Bases: tuple
A class to create a callable from a list of words. The concatenation of a list of words is obtained by creating a word from this callable.
Bases: list
A list subclass having a nicer representation for factorization of words.
TESTS:
sage: f = sage.combinat.words.finite_word.Factorization()
sage: f == loads(dumps(f))
True
Bases: sage.combinat.words.abstract_word.Word_class
Returns the Burrows-Wheeler Transform (BWT) of self.
The Burrows-Wheeler transform of a finite word  is obtained
from
is obtained
from  by first listing the conjugates of
by first listing the conjugates of  in lexicographic order
and then concatenating the final letters of the conjugates in this
order. See [1].
in lexicographic order
and then concatenating the final letters of the conjugates in this
order. See [1].
EXAMPLES:
sage: Word('abaccaaba').BWT()
word: cbaabaaca
sage: Word('abaab').BWT()
word: bbaaa
sage: Word('bbabbaca').BWT()
word: cbbbbaaa
sage: Word('aabaab').BWT()
word: bbaaaa
sage: Word().BWT()
word:
sage: Word('a').BWT()
word: a
REFERENCES:
Return the word obtained by applying permutation to the letters of the alphabet of self.
EXAMPLES:
sage: w = Words('abcd')('abcd')
sage: p = [2,1,4,3]
sage: w.apply_permutation_to_letters(p)
word: badc
sage: u = Words('dabc')('abcd')
sage: u.apply_permutation_to_letters(p)
word: dcba
sage: w.apply_permutation_to_letters(Permutation(p))
word: badc
sage: w.apply_permutation_to_letters(PermutationGroupElement(p))
word: badc
Return the word obtained by permuting the positions of the letters in self.
EXAMPLES:
sage: w = Words('abcd')('abcd')
sage: w.apply_permutation_to_positions([2,1,4,3])
word: badc
sage: u = Words('dabc')('abcd')
sage: u.apply_permutation_to_positions([2,1,4,3])
word: badc
sage: w.apply_permutation_to_positions(Permutation([2,1,4,3]))
word: badc
sage: w.apply_permutation_to_positions(PermutationGroupElement([2,1,4,3]))
word: badc
sage: Word([1,2,3,4]).apply_permutation_to_positions([3,4,2,1])
word: 3421
Returns the longest word that is both a proper prefix and a proper suffix of self.
EXAMPLES:
sage: Word('121212').border()
word: 1212
sage: Word('12321').border()
word: 1
sage: Word().border() is None
True
EXAMPLES:
sage: Word([1,1,2,2,3]).charge()
0
sage: Word([3,1,1,2,2]).charge()
1
sage: Word([2,1,1,2,3]).charge()
1
sage: Word([2,1,1,3,2]).charge()
2
sage: Word([3,2,1,1,2]).charge()
2
sage: Word([2,2,1,1,3]).charge()
3
sage: Word([3,2,2,1,1]).charge()
4
TESTS:
sage: Word([3,3,2,1,1]).charge()
...
ValueError: the evaluation of the word must be a partition
Tries to return a pair of words with a common parent; raises an exception if this is not possible.
This function begins by checking if both words have the same parent. If this is the case, then no work is done and both words are returned as-is.
Otherwise it will attempt to convert other to the domain of self. If that fails, it will attempt to convert self to the domain of other. If both attempts fail, it raises a TypeError to signal failure.
EXAMPLES:
sage: W1 = Words('abc'); W2 = Words('ab')
sage: w1 = W1('abc'); w2 = W2('abba'); w3 = W1('baab')
sage: w1.parent() is w2.parent()
False
sage: a, b = w1.coerce(w2)
sage: a.parent() is b.parent()
True
sage: w1.parent() is w2.parent()
False
Returns a vector (Graphics object) illustrating self. Each letter is represented by a coloured rectangle.
If the parent of self is a class of words over a finite alphabet, then each letter in the alphabet is assigned a unique colour, and this colour will be the same every time this method is called. This is especially useful when plotting and comparing words defined on the same alphabet.
If the alphabet is infinite, then the letters appearing in the word are used as the alphabet.
INPUT:
x - (default: 0) bottom left x-coordinate of the vector
y - (default: 0) bottom left y-coordinate of the vector
width - (default: ‘default’) width of the vector. By default, the width is the length of self.
height - (default: 1) height of the vector
thickness - (default: 1) thickness of the contour
type: import matplotlib.cm; matplotlib.cm.datad.keys()
label - str (default: None) a label to add on the colored vector.
OUTPUT:
Graphics
EXAMPLES:
sage: Word(range(20)).colored_vector()
sage: Word(range(100)).colored_vector(0,0,10,1)
sage: Words(range(100))(range(10)).colored_vector()
sage: w = Word('abbabaab')
sage: w.colored_vector()
sage: w.colored_vector(cmap='autumn')
sage: Word(range(20)).colored_vector(label='Rainbow')
When two words are defined under the same parent, same letters are mapped to same colors:
sage: W = Words(range(20))
sage: w = W(range(20))
sage: y = W(range(10,20))
sage: y.colored_vector(y=1, x=10) + w.colored_vector()
TESTS:
The empty word:
sage: Word().colored_vector()
sage: Word().colored_vector(label='empty')
Unknown cmap:
sage: Word(range(100)).colored_vector(cmap='jolies')
...
RuntimeError: Color map jolies not known
sage: Word(range(100)).colored_vector(cmap='__doc__')
...
RuntimeError: Color map __doc__ not known
Returns True if self commutes with other, and False otherwise.
EXAMPLES:
sage: Word('12').commutes_with(Word('12'))
True
sage: Word('12').commutes_with(Word('11'))
False
sage: Word().commutes_with(Word('21'))
True
Returns the set of complete return words of fact in self.
This is the set of all factors starting by the given factor and ending just after the next occurrence of this factor. See for instance [1].
EXAMPLES:
sage: s = Word('21331233213231').complete_return_words(Word('2'))
sage: sorted(s)
[word: 2132, word: 213312, word: 2332]
sage: Word('').complete_return_words(Word('213'))
set([])
sage: Word('121212').complete_return_words(Word('1212'))
set([word: 121212])
REFERENCES:
Returns the concatenation of self and other.
INPUT:
EXAMPLES:
Concatenation may be made using + or * operations:
sage: w = Word('abadafd')
sage: y = Word([5,3,5,8,7])
sage: w * y
word: abadafd53587
sage: w + y
word: abadafd53587
sage: w.concatenate(y)
word: abadafd53587
Both words must be defined over the same alphabet:
sage: z = Word('12223', alphabet = '123')
sage: z + y
...
ValueError: 5 not in alphabet!
Eventually, it should work:
sage: z = Word('12223', alphabet = '123')
sage: z + y #todo: not implemented
word: 1222353587
TESTS:
The empty word is not considered by concatenation:
sage: type(Word([]) * Word('abcd'))
<class 'sage.combinat.words.word.FiniteWord_str'>
sage: type(Word('abcd') * Word())
<class 'sage.combinat.words.word.FiniteWord_str'>
sage: type(Word('abcd') * Word([]))
<class 'sage.combinat.words.word.FiniteWord_str'>
sage: type(Word('abcd') * Word(()))
<class 'sage.combinat.words.word.FiniteWord_str'>
sage: type(Word([1,2,3]) * Word(''))
<class 'sage.combinat.words.word.FiniteWord_list'>
Returns the conjugate at pos of self.
pos can be any integer, the distance used is the modulo by the length of self.
EXAMPLES:
sage: Word('12112').conjugate(1)
word: 21121
sage: Word().conjugate(2)
word:
sage: Word('12112').conjugate(8)
word: 12121
sage: Word('12112').conjugate(-1)
word: 21211
Returns the position where self is conjugate with other. Returns None if there is no such position.
EXAMPLES:
sage: Word('12113').conjugate_position(Word('31211'))
1
sage: Word('12131').conjugate_position(Word('12113')) is None
True
sage: Word().conjugate_position(Word('123')) is None
True
Returns the set of conjugates of self.
TESTS:
sage: Word('cbbca').conjugates() == set([Word('cacbb'),Word('bbcac'),Word('acbbc'),Word('cbbca'),Word('bcacb')])
True
sage: Word('abcabc').conjugates() == set([Word('abcabc'),Word('bcabca'),Word('cabcab')])
True
sage: Word().conjugates() == set([Word()])
True
sage: Word('a').conjugates() == set([Word('a')])
True
Counts the number of occurrences of letter in self.
EXAMPLES:
sage: Word('abbabaab').count('a')
4
Returns the critical exponent of self.
The critical exponent of a word is the supremum of the order of all its (finite) factors. See [1].
Note
The implementation here uses the suffix tree to enumerate all the factors. It should be improved.
EXAMPLES:
sage: Word('aaba').critical_exponent()
2
sage: Word('aabaa').critical_exponent()
2
sage: Word('aabaaba').critical_exponent()
7/3
sage: Word('ab').critical_exponent()
1
sage: Word('aba').critical_exponent()
3/2
sage: words.ThueMorseWord()[:20].critical_exponent()
2
REFERENCES:
Returns the Crochemore factorization of self as an ordered list of factors.
The Crochemore factorization of a finite word  is the unique
factorization:
is the unique
factorization: 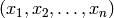 of
of  with each
with each 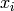 satisfying either:
C1.
satisfying either:
C1. 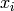 is a letter that does not appear in
is a letter that does not appear in 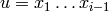 ;
C2.
;
C2. 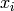 is the longest prefix of
is the longest prefix of 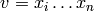 that also
has an occurrence beginning within
that also
has an occurrence beginning within 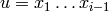 . See [1].
. See [1].
Note
This is not a very good implementation, and should be improved.
EXAMPLES:
sage: x = Word('abababb')
sage: x.crochemore_factorization()
(a, b, abab, b)
sage: mul(x.crochemore_factorization()) == x
True
sage: y = Word('abaababacabba')
sage: y.crochemore_factorization()
(a, b, a, aba, ba, c, ab, ba)
sage: mul(y.crochemore_factorization()) == y
True
sage: x = Word([0,1,0,1,0,1,1])
sage: x.crochemore_factorization()
(0, 1, 0101, 1)
sage: mul(x.crochemore_factorization()) == x
True
REFERENCES:
Returns the defect of self.
The defect of a finite word  is given by
is given by
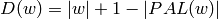 , where
, where 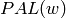 denotes the set of palindromic
factors of
denotes the set of palindromic
factors of  (including the empty word). See [1].
(including the empty word). See [1].
INPUT:
OUTPUT:
- integer – If f is None, the palindromic defect of self;
- otherwise, the f-palindromic defect of self.
EXAMPLES:
sage: words.ThueMorseWord()[:100].defect()
16
sage: words.FibonacciWord()[:100].defect()
0
sage: Word('000000000000').defect()
0
sage: Word('011010011001').defect()
2
sage: Word('0101001010001').defect()
0
sage: Word().defect()
0
sage: Word('abbabaabbaababba').defect()
2
sage: f = WordMorphism('a->b,b->a')
sage: Word('abbabaabbaababba').defect(f)
4
REFERENCES:
Returns True if the word self is degree inverse lexicographically less than other.
EXAMPLES:
sage: Word([1,2,4]).deg_inv_lex_less(Word([1,3,2]))
False
sage: Word([3,2,1]).deg_inv_lex_less(Word([1,2,3]))
True
Returns True if self is degree lexicographically less than other, and False otherwise. The weight of each letter in the ordered alphabet is given by weights, which defaults to [1, 2, 3, ...].
EXAMPLES:
sage: Word([1,2,3]).deg_lex_less(Word([1,3,2]))
True
sage: Word([3,2,1]).deg_lex_less(Word([1,2,3]))
False
sage: W = Words(range(5))
sage: W([1,2,4]).deg_lex_less(W([1,3,2]))
False
sage: Word("abba").deg_lex_less(Word("abbb"), dict(a=1,b=2))
True
sage: Word("abba").deg_lex_less(Word("baba"), dict(a=1,b=2))
True
sage: Word("abba").deg_lex_less(Word("aaba"), dict(a=1,b=2))
False
sage: Word("abba").deg_lex_less(Word("aaba"), dict(a=1,b=0))
True
Returns True if self is degree reverse lexicographically less than other.
EXAMPLES:
sage: Word([3,2,1]).deg_rev_lex_less(Word([1,2,3]))
False
sage: Word([1,2,4]).deg_rev_lex_less(Word([1,3,2]))
False
sage: Word([1,2,3]).deg_rev_lex_less(Word([1,2,4]))
True
Returns the weighted degree of self, where the weighted degree of each letter in the ordered alphabet is given by weights, which defaults to [1, 2, 3, ...].
INPUTS:
EXAMPLES:
sage: Word([1,2,3]).degree()
6
sage: Word([3,2,1]).degree()
6
sage: Words("ab")("abba").degree()
6
sage: Words("ab")("abba").degree([0,2])
4
sage: Words("ab")("abba").degree([-1,-1])
-4
sage: Words("ab")("aabba").degree([1,1])
5
sage: Words([1,2,4])([1,2,4]).degree()
6
sage: Word([1,2,4]).degree()
7
sage: Word("aabba").degree({'a':1,'b':2})
7
sage: Word([0,1,0]).degree({0:17,1:0})
34
Returns the image of self under the delta morphism. This is the word composed of the length of consecutive runs of the same letter in a given word.
EXAMPLES:
sage: W = Words('0123456789')
sage: W('22112122').delta()
word: 22112
sage: W('555008').delta()
word: 321
sage: W().delta()
word:
sage: Word('aabbabaa').delta()
word: 22112
Returns the derivative under delta for self.
EXAMPLES:
sage: W = Words('12')
sage: W('12211').delta_derivate()
word: 22
sage: W('1').delta_derivate(Words([1]))
word: 1
sage: W('2112').delta_derivate()
word: 2
sage: W('2211').delta_derivate()
word: 22
sage: W('112').delta_derivate()
word: 2
sage: W('11222').delta_derivate(Words([1, 2, 3]))
word: 3
Returns the derivative under delta for self.
EXAMPLES:
sage: W = Words('12')
sage: W('12211').delta_derivate_left()
word: 22
sage: W('1').delta_derivate_left(Words([1]))
word: 1
sage: W('2112').delta_derivate_left()
word: 21
sage: W('2211').delta_derivate_left()
word: 22
sage: W('112').delta_derivate_left()
word: 21
sage: W('11222').delta_derivate_left(Words([1, 2, 3]))
word: 3
Returns the right derivative under delta for self.
EXAMPLES:
sage: W = Words('12')
sage: W('12211').delta_derivate_right()
word: 122
sage: W('1').delta_derivate_right(Words([1]))
word: 1
sage: W('2112').delta_derivate_right()
word: 12
sage: W('2211').delta_derivate_right()
word: 22
sage: W('112').delta_derivate_right()
word: 2
sage: W('11222').delta_derivate_right(Words([1, 2, 3]))
word: 23
Lifts self via the delta operator to obtain a word containing the letters in alphabet (default is [0, 1]). The letters used in the construction start with s (default is alphabet[0]) and cycle through alphabet.
INPUT:
EXAMPLES:
sage: W = Words([1, 2])
sage: W([2, 2, 1, 1]).delta_inv()
word: 112212
sage: W([1, 1, 1, 1]).delta_inv(Words('123'))
word: 1231
sage: W([2, 2, 1, 1, 2]).delta_inv(s=2)
word: 22112122
Returns the Parikh vector of self, i.e., the vector containing the number of occurrences of each letter, given in the order of the alphabet.
See also evaluation_dict.
INPUT:
EXAMPLES:
sage: Words('ab')().parikh_vector()
[0, 0]
sage: Word('aabaa').parikh_vector('abc')
[4, 1, 0]
sage: Word('a').parikh_vector('abc')
[1, 0, 0]
sage: Word('a').parikh_vector('cab')
[0, 1, 0]
sage: Word('a').parikh_vector('bca')
[0, 0, 1]
sage: Word().parikh_vector('ab')
[0, 0]
sage: Word().parikh_vector('abc')
[0, 0, 0]
sage: Word().parikh_vector('abcd')
[0, 0, 0, 0]
TESTS:
sage: Word('aabaa').parikh_vector()
...
TypeError: the alphabet is infinite; specify a finite alphabet or use evaluation_dict() instead
Returns a dictionary keyed by the letters occurring in self with values the number of occurrences of the letter.
EXAMPLES:
sage: Word([2,1,4,2,3,4,2]).evaluation_dict()
{1: 1, 2: 3, 3: 1, 4: 2}
sage: Word('badbcdb').evaluation_dict()
{'a': 1, 'c': 1, 'b': 3, 'd': 2}
sage: Word().evaluation_dict()
{}
Returns the evaluation of the word w as a partition.
EXAMPLES:
sage: Word("acdabda").evaluation_partition()
[3, 2, 1, 1]
sage: Word([2,1,4,2,3,4,2]).evaluation_partition()
[3, 2, 1, 1]
Returns a list representing the evaluation of self. The entries of the list are two-element lists [a, n], where a is a letter occurring in self and n is the number of occurrences of a in self.
EXAMPLES:
sage: Word([4,4,2,5,2,1,4,1]).evaluation_sparse()
[(1, 2), (2, 2), (4, 3), (5, 1)]
sage: Word("abcaccab").evaluation_sparse()
[('a', 3), ('c', 3), ('b', 2)]
Returns the exponent of self.
OUTPUT:
integer – the exponent
EXAMPLES:
sage: Word('1231').exponent()
1
sage: Word('121212').exponent()
3
sage: Word().exponent()
0
Generates distinct factors of self.
INPUT:
OUTPUT:
If n is an integer, returns an iterator over all distinct factors of length n. If n is None, returns an iterator generating all distinct factors.
EXAMPLES:
sage: w = Word('1213121')
sage: sorted( w.factor_iterator(0) )
[word: ]
sage: sorted( w.factor_iterator(10) )
[]
sage: sorted( w.factor_iterator(1) )
[word: 1, word: 2, word: 3]
sage: sorted( w.factor_iterator(4) )
[word: 1213, word: 1312, word: 2131, word: 3121]
sage: sorted( w.factor_iterator() )
[word: , word: 1, word: 12, word: 121, word: 1213, word: 12131, word: 121312, word: 1213121, word: 13, word: 131, word: 1312, word: 13121, word: 2, word: 21, word: 213, word: 2131, word: 21312, word: 213121, word: 3, word: 31, word: 312, word: 3121]
sage: u = Word([1,2,1,2,3])
sage: sorted( u.factor_iterator(0) )
[word: ]
sage: sorted( u.factor_iterator(10) )
[]
sage: sorted( u.factor_iterator(1) )
[word: 1, word: 2, word: 3]
sage: sorted( u.factor_iterator(5) )
[word: 12123]
sage: sorted( u.factor_iterator() )
[word: , word: 1, word: 12, word: 121, word: 1212, word: 12123, word: 123, word: 2, word: 21, word: 212, word: 2123, word: 23, word: 3]
sage: xxx = Word("xxx")
sage: sorted( xxx.factor_iterator(0) )
[word: ]
sage: sorted( xxx.factor_iterator(4) )
[]
sage: sorted( xxx.factor_iterator(2) )
[word: xx]
sage: sorted( xxx.factor_iterator() )
[word: , word: x, word: xx, word: xxx]
sage: e = Word()
sage: sorted( e.factor_iterator(0) )
[word: ]
sage: sorted( e.factor_iterator(17) )
[]
sage: sorted( e.factor_iterator() )
[word: ]
TESTS:
sage: type( Word('cacao').factor_iterator() )
<type 'generator'>
Returns an iterator over all occurrences (including overlapping ones) of self in other in their order of appearance.
EXAMPLES:
sage: u = Word('121')
sage: w = Word('121213211213')
sage: list(u.factor_occurrences_in(w))
[0, 2, 8]
Returns the set of factors (of length n) of self.
INPUT:
OUTPUT:
If n is an integer, returns the set of all distinct factors of length n. If n is None, returns the set of all distinct factors.
EXAMPLES:
sage: w = Word('121')
sage: s = w.factor_set()
sage: sorted(s)
[word: , word: 1, word: 12, word: 121, word: 2, word: 21]
sage: w = Word('1213121')
sage: for i in range(w.length()): sorted(w.factor_set(i))
[word: ]
[word: 1, word: 2, word: 3]
[word: 12, word: 13, word: 21, word: 31]
[word: 121, word: 131, word: 213, word: 312]
[word: 1213, word: 1312, word: 2131, word: 3121]
[word: 12131, word: 13121, word: 21312]
[word: 121312, word: 213121]
sage: w = Word([1,2,1,2,3])
sage: s = w.factor_set()
sage: sorted(s)
[word: , word: 1, word: 12, word: 121, word: 1212, word: 12123, word: 123, word: 2, word: 21, word: 212, word: 2123, word: 23, word: 3]
TESTS:
sage: w = Word("xx")
sage: s = w.factor_set()
sage: sorted(s)
[word: , word: x, word: xx]
sage: Set(Word().factor_set())
{word: }
Returns the index of the first occurrence of sub in self, such that sub is contained within self[start:end]. Returns -1 on failure.
INPUT:
OUTPUT:
non negative integer or -1
EXAMPLES:
sage: w = Word([0,1,0,0,1])
sage: w.find(Word([0,1]))
0
sage: w.find(Word([0,1]), start=1)
3
sage: w.find(Word([0,1]), start=1, end=5)
3
sage: w.find(Word([0,1]), start=1, end=4) == -1
True
sage: w.find(Word([1,1])) == -1
True
Instances of Word_str handle string inputs as well:
sage: w = Word('abac')
sage: w.find('a')
0
sage: w.find(Word('a'))
0
Returns the position of the first occurrence of self in other, or None if self is not a factor of other.
EXAMPLES:
sage: Word('12').first_pos_in(Word('131231'))
2
sage: Word('32').first_pos_in(Word('131231')) is None
True
Returns a table of the frequencies of the letters in self.
OUTPUT:
dict – letters associated to their frequency
EXAMPLES:
sage: f = Word('1213121').freq()
doctest:1: DeprecationWarning: freq is deprecated, use evaluation_dict instead!
sage: f # keys appear in random order
{'1': 4, '2': 2, '3': 1}
TESTS:
sage: f = Word('1213121').freq()
sage: f['1'] == 4
True
sage: f['2'] == 2
True
sage: f['3'] == 1
True
Returns a table of the maximum skip you can do in order not to miss a possible occurrence of self in a word.
This is a part of the Boyer-Moore algorithm to find factors. See [1].
EXAMPLES:
sage: Word('121321').good_suffix_table()
[5, 5, 5, 5, 3, 3, 1]
sage: Word('12412').good_suffix_table()
[3, 3, 3, 3, 3, 1]
REFERENCES:
Test whether self has other as a prefix.
INPUT:
- other - a word, or data describing a word
OUTPUT:
- boolean
EXAMPLES:
sage: w = Word("abbabaabababa")
sage: u = Word("abbab")
sage: w.has_prefix(u)
True
sage: u.has_prefix(w)
False
sage: u.has_prefix("abbab")
True
sage: w = Word([0,1,1,0,1,0,0,1,0,1,0,1,0])
sage: u = Word([0,1,1,0,1])
sage: w.has_prefix(u)
True
sage: u.has_prefix(w)
False
sage: u.has_prefix([0,1,1,0,1])
True
Test whether self has other as a suffix.
Note
Some word datatype classes, like WordDatatype_str, override this method.
INPUT:
- other - a word, or data describing a word
OUTPUT:
- boolean
EXAMPLES:
sage: w = Word("abbabaabababa")
sage: u = Word("ababa")
sage: w.has_suffix(u)
True
sage: u.has_suffix(w)
False
sage: u.has_suffix("ababa")
True
sage: w = Word([0,1,1,0,1,0,0,1,0,1,0,1,0])
sage: u = Word([0,1,0,1,0])
sage: w.has_suffix(u)
True
sage: u.has_suffix(w)
False
sage: u.has_suffix([0,1,0,1,0])
True
Returns the implicit suffix tree of self.
The suffix tree of a word  is a compactification of the
suffix trie for
is a compactification of the
suffix trie for  . The compactification removes all nodes that have
exactly one incoming edge and exactly one outgoing edge. It consists of
two components: a tree and a word. Thus, instead of labelling the edges
by factors of
. The compactification removes all nodes that have
exactly one incoming edge and exactly one outgoing edge. It consists of
two components: a tree and a word. Thus, instead of labelling the edges
by factors of  , we can labelled them by indices of the occurrence of
the factors in
, we can labelled them by indices of the occurrence of
the factors in  .
.
See sage.combinat.words.suffix_trees.ImplicitSuffixTree? for more information.
EXAMPLES:
sage: w = Word("cacao")
sage: w.implicit_suffix_tree()
Implicit Suffix Tree of the word: cacao
sage: w = Word([0,1,0,1,1])
sage: w.implicit_suffix_tree()
Implicit Suffix Tree of the word: 01011
Returns True if self is inverse lexicographically less than other.
EXAMPLES:
sage: Word([1,2,4]).inv_lex_less(Word([1,3,2]))
False
sage: Word([3,2,1]).inv_lex_less(Word([1,2,3]))
True
Returns a list of the inversions of self. An inversion is a pair (i,j) of non-negative integers i < j such that self[i] > self[j].
EXAMPLES:
sage: Word([1,2,3,2,2,1]).inversions()
[[1, 5], [2, 3], [2, 4], [2, 5], [3, 5], [4, 5]]
sage: Words([3,2,1])([1,2,3,2,2,1]).inversions()
[[0, 1], [0, 2], [0, 3], [0, 4], [1, 2]]
sage: Word('abbaba').inversions()
[[1, 3], [1, 5], [2, 3], [2, 5], [4, 5]]
sage: Words('ba')('abbaba').inversions()
[[0, 1], [0, 2], [0, 4], [3, 4]]
Returns True if self is  -balanced, and False otherwise.
-balanced, and False otherwise.
A finite or infinite word  is said to be `q`-balanced if for
any two factors
is said to be `q`-balanced if for
any two factors  ,
,  of
of  of the same length, the difference
between the number of
of the same length, the difference
between the number of  ‘s in each of
‘s in each of  and
and  is at most
is at most  for all letters
for all letters  in the alphabet of
in the alphabet of  . A
. A  -balanced word is
simply said to be balanced. See for instance [1] and Chapter 2 of
[2].
-balanced word is
simply said to be balanced. See for instance [1] and Chapter 2 of
[2].
INPUT:
OUTPUT:
boolean – the result
EXAMPLES:
sage: Word('1213121').is_balanced()
True
sage: Word('1122').is_balanced()
False
sage: Word('121333121').is_balanced()
False
sage: Word('121333121').is_balanced(2)
False
sage: Word('121333121').is_balanced(3)
True
sage: Word('121122121').is_balanced()
False
sage: Word('121122121').is_balanced(2)
True
TESTS:
sage: Word('121122121').is_balanced(-1)
...
TypeError: the balance level must be a positive integer
sage: Word('121122121').is_balanced(0)
...
TypeError: the balance level must be a positive integer
sage: Word('121122121').is_balanced('a')
...
TypeError: the balance level must be a positive integer
REFERENCES:
Returns True if seq is a cadence of self, and False otherwise.
A cadence is an increasing sequence of indexes that all map to the same letter.
EXAMPLES:
sage: Word('121132123').is_cadence([0, 2, 6])
True
sage: Word('121132123').is_cadence([0, 1, 2])
False
sage: Word('121132123').is_cadence([])
True
Returns True if self is a conjugate of other, and False otherwise.
EXAMPLES:
sage: Word('11213').is_conjugate_with(Word('31121'))
True
sage: Word().is_conjugate_with(Word('123'))
False
sage: Word('112131').is_conjugate_with(Word('11213'))
False
sage: Word('12131').is_conjugate_with(Word('11213'))
True
Returns True if self is a cube, and False otherwise.
EXAMPLES:
sage: Word('012012012').is_cube()
True
sage: Word('01010101').is_cube()
False
sage: Word().is_cube()
True
sage: Word('012012').is_cube()
False
Returns True if self does not contain cubes, and False otherwise.
EXAMPLES:
sage: Word('12312').is_cube_free()
True
sage: Word('32221').is_cube_free()
False
sage: Word().is_cube_free()
True
TESTS:
We make sure that #8490 is fixed:
sage: Word('111').is_cube_free()
False
sage: Word('2111').is_cube_free()
False
sage: Word('32111').is_cube_free()
False
Returns True if the length of self is zero, and False otherwise.
EXAMPLES:
sage: Word([]).is_empty()
True
sage: Word('a').is_empty()
False
Returns True if self is a factor of other, and False otherwise.
EXAMPLES:
sage: u = Word('2113')
sage: w = Word('123121332131233121132123')
sage: u.is_factor(w)
True
sage: u = Word('321')
sage: w = Word('1231241231312312312')
sage: u.is_factor(w)
False
The empty word is factor of another word:
sage: Word().is_factor(Word())
True
sage: Word().is_factor(Word('a'))
True
sage: Word().is_factor(Word([1,2,3]))
True
sage: Word().is_factor(Word(lambda n:n, length=5))
True
Returns True if self is a factor of other, and False otherwise.
EXAMPLES:
sage: u = Word('2113')
sage: w = Word('123121332131233121132123')
sage: u.is_factor_of(w)
doctest:1: DeprecationWarning: is_factor_of is deprecated, use is_factor instead!
True
sage: u = Word('321')
sage: w = Word('1231241231312312312')
sage: u.is_factor_of(w)
False
Returns True if self has defect 0, and False otherwise.
A word is full if its defect is zero (see [1]).
INPUT:
OUTPUT:
- boolean – If f is None, whether self is full;
- otherwise, whether self is full of
-palindromes.
EXAMPLES:
sage: words.ThueMorseWord()[:100].is_full()
False
sage: words.FibonacciWord()[:100].is_full()
True
sage: Word('000000000000000').is_full()
True
sage: Word('011010011001').is_full()
False
sage: Word('2194').is_full()
True
sage: Word().is_full()
True
sage: f = WordMorphism('a->b,b->a')
sage: Word().is_full(f)
True
sage: w = Word('ab')
sage: w.is_full()
True
sage: w.is_full(f)
False
REFERENCES:
Returns True if self is a Lyndon word, and False otherwise.
A Lyndon word is a non-empty word that is lexicographically
smaller than all of its proper suffixes for the given order
on its alphabet. That is,  is a Lyndon word if
is a Lyndon word if  is non-empty
and for each factorization
is non-empty
and for each factorization 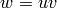 (with
(with  ,
,  both non-empty),
we have
both non-empty),
we have 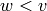 .
.
Equivalently,  is a Lyndon word iff
is a Lyndon word iff  is a non-empty word that is
lexicographically smaller than all of its proper conjugates for the
given order on its alphabet.
is a non-empty word that is
lexicographically smaller than all of its proper conjugates for the
given order on its alphabet.
See for instance [1].
EXAMPLES:
sage: Word('123132133').is_lyndon()
True
sage: Word().is_lyndon()
True
sage: Word('122112').is_lyndon()
False
TESTS:
A sanity check: LyndonWords generates Lyndon words, so we
filter all words of length 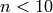 on the alphabet [1,2,3] for
Lyndon words, and compare with the LyndonWords generator:
on the alphabet [1,2,3] for
Lyndon words, and compare with the LyndonWords generator:
sage: for n in range(1,10):
... lw1 = [w for w in Words([1,2,3], n) if w.is_lyndon()]
... lw2 = LyndonWords(3,n)
... if set(lw1) != set(lw2): print False
Filter all words of length 8 on the alphabet [c,a,b] for Lyndon words, and compare with the LyndonWords generator after mapping [a,b,c] to [2,3,1]:
sage: lw = [w for w in Words('cab', 8) if w.is_lyndon()]
sage: phi = WordMorphism({'a':2,'b':3,'c':1})
sage: set(map(phi, lw)) == set(LyndonWords(3,8))
True
REFERENCES:
Returns True if self is an overlap, and False otherwise.
EXAMPLES:
sage: Word('12121').is_overlap()
True
sage: Word('123').is_overlap()
False
sage: Word('1231').is_overlap()
False
sage: Word('123123').is_overlap()
False
sage: Word('1231231').is_overlap()
True
sage: Word().is_overlap()
False
Returns True if self is a palindrome (or a  -palindrome), and
False otherwise.
-palindrome), and
False otherwise.
Let 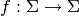 be an involution that extends
to a morphism on
be an involution that extends
to a morphism on 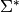 . We say that
. We say that 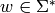 is a
`f`-palindrome if
is a
`f`-palindrome if 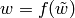 [1]. Also called
`f`-pseudo-palindrome [2].
[1]. Also called
`f`-pseudo-palindrome [2].
INPUT:
EXAMPLES:
sage: Word('esope reste ici et se repose').is_palindrome()
False
sage: Word('esoperesteicietserepose').is_palindrome()
True
sage: Word('I saw I was I').is_palindrome()
True
sage: Word('abbcbba').is_palindrome()
True
sage: Word('abcbdba').is_palindrome()
False
Some  -palindromes:
-palindromes:
sage: f = WordMorphism('a->b,b->a')
sage: Word('aababb').is_palindrome(f)
True
sage: f = WordMorphism('a->b,b->a,c->c')
sage: Word('abacbacbab').is_palindrome(f)
True
sage: f = WordMorphism({'a':'b','b':'a'})
sage: Word('aababb').is_palindrome(f)
True
sage: f = WordMorphism({0:[1],1:[0]})
sage: w = words.ThueMorseWord()[:8]; w
word: 01101001
sage: w.is_palindrome(f)
True
The word must be in the domain of the involution:
sage: f = WordMorphism('a->a')
sage: Word('aababb').is_palindrome(f)
...
KeyError: 'b'
TESTS:
If the given involution is not an involution:
sage: f = WordMorphism('a->b,b->b')
sage: Word('abab').is_palindrome(f)
...
ValueError: f must be an involution
sage: Y = Word
sage: Y().is_palindrome()
True
sage: Y('a').is_palindrome()
True
sage: Y('ab').is_palindrome()
False
sage: Y('aba').is_palindrome()
True
sage: Y('aa').is_palindrome()
True
sage: E = WordMorphism('a->b,b->a')
sage: Y().is_palindrome(E)
True
sage: Y('a').is_palindrome(E)
False
sage: Y('ab').is_palindrome(E)
True
sage: Y('aa').is_palindrome(E)
False
sage: Y('aba').is_palindrome(E)
False
sage: Y('abab').is_palindrome(E)
True
REFERENCES:
 -palindromes,
Mémoire de maîtrise en Mathématiques, Montréal, UQAM, 2008,
109 pages.
-palindromes,
Mémoire de maîtrise en Mathématiques, Montréal, UQAM, 2008,
109 pages.Returns True if self is a prefix of other, and False otherwise.
EXAMPLES:
sage: w = Word('0123456789')
sage: y = Word('012345')
sage: y.is_prefix(w)
True
sage: w.is_prefix(y)
False
sage: w.is_prefix(Word())
False
sage: Word().is_prefix(w)
True
sage: Word().is_prefix(Word())
True
Returns True if self is a prefix of other, and False otherwise.
EXAMPLES:
sage: w = Word('0123456789')
sage: y = Word('012345')
sage: y.is_prefix_of(w)
doctest:1: DeprecationWarning: is_prefix_of is deprecated, use is_prefix instead!
True
sage: w.is_prefix_of(y)
False
sage: w.is_prefix_of(Word())
False
sage: Word().is_prefix_of(w)
True
sage: Word().is_prefix_of(Word())
True
Returns True if self is primitive, and False otherwise.
A finite word  is primitive if it is not a positive integer
power of a shorter word.
is primitive if it is not a positive integer
power of a shorter word.
EXAMPLES:
sage: Word('1231').is_primitive()
True
sage: Word('111').is_primitive()
False
Returns True if self is a proper prefix of other, and False otherwise.
EXAMPLES:
sage: Word('12').is_proper_prefix(Word('123'))
True
sage: Word('12').is_proper_prefix(Word('12'))
False
sage: Word().is_proper_prefix(Word('123'))
True
sage: Word('123').is_proper_prefix(Word('12'))
False
sage: Word().is_proper_prefix(Word())
False
Returns True if self is a proper prefix of other, and False otherwise.
EXAMPLES:
sage: Word('12').is_proper_prefix_of(Word('123'))
doctest:1: DeprecationWarning: is_proper_prefix_of is deprecated, use is_proper_prefix instead!
doctest:...: DeprecationWarning: is_prefix_of is deprecated, use is_prefix instead!
True
sage: Word('12').is_proper_prefix_of(Word('12'))
False
sage: Word().is_proper_prefix_of(Word('123'))
True
sage: Word('123').is_proper_prefix_of(Word('12'))
False
sage: Word().is_proper_prefix_of(Word())
False
Returns True if self is a proper suffix of other, and False otherwise.
EXAMPLES:
sage: Word('23').is_proper_suffix(Word('123'))
True
sage: Word('12').is_proper_suffix(Word('12'))
False
sage: Word().is_proper_suffix(Word('123'))
True
sage: Word('123').is_proper_suffix(Word('12'))
False
Returns True if self is a proper suffix of other, and False otherwise.
EXAMPLES:
sage: Word('23').is_proper_suffix_of(Word('123'))
doctest:1: DeprecationWarning: is_proper_suffix_of is deprecated, use is_proper_suffix instead!
doctest:...: DeprecationWarning: is_suffix_of is deprecated, use is_suffix instead!
True
sage: Word('12').is_proper_suffix_of(Word('12'))
False
sage: Word().is_proper_suffix_of(Word('123'))
True
sage: Word('123').is_proper_suffix_of(Word('12'))
False
Returns True if self is quasiperiodic, and False otherwise.
A finite or infinite word  is quasiperiodic if it can be
constructed by concatenations and superpositions of one of its proper
factors
is quasiperiodic if it can be
constructed by concatenations and superpositions of one of its proper
factors  , which is called a quasiperiod of
, which is called a quasiperiod of  .
See for instance [1], [2], and [3].
.
See for instance [1], [2], and [3].
EXAMPLES:
sage: Word('abaababaabaababaaba').is_quasiperiodic()
True
sage: Word('abacaba').is_quasiperiodic()
False
sage: Word('a').is_quasiperiodic()
False
sage: Word().is_quasiperiodic()
False
sage: Word('abaaba').is_quasiperiodic()
True
REFERENCES:
Returns True if self is the prefix of a smooth word, and False otherwise.
Let 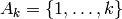 ,
, 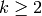 . An infinite word
. An infinite word  in
in
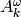 is said to be smooth if and only if for all positive
integers
is said to be smooth if and only if for all positive
integers  ,
, 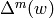 is in
is in 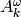 , where
, where 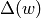 is
the word obtained from
is
the word obtained from  by composing the length of consecutive
runs of the same letter in
by composing the length of consecutive
runs of the same letter in  . See for instance [1] and [2].
. See for instance [1] and [2].
INPUT:
OUTPUT:
boolean – whether self is a smooth prefix or not
EXAMPLES:
sage: W = Words([1, 2])
sage: W([1, 1, 2, 2, 1, 2, 1, 1]).is_smooth_prefix()
True
sage: W([1, 2, 1, 2, 1, 2]).is_smooth_prefix()
False
REFERENCES:
Returns True if self is a square, and False otherwise.
EXAMPLES:
sage: Word([1,0,0,1]).is_square()
False
sage: Word('1212').is_square()
True
sage: Word('1213').is_square()
False
sage: Word('12123').is_square()
False
sage: Word().is_square()
True
Returns True if self does not contain squares, and False otherwise.
EXAMPLES:
sage: Word('12312').is_square_free()
True
sage: Word('31212').is_square_free()
False
sage: Word().is_square_free()
True
TESTS:
We make sure that #8490 is fixed:
sage: Word('11').is_square_free()
False
sage: Word('211').is_square_free()
False
sage: Word('3211').is_square_free()
False
Returns True is self is a subword of other, and False otherwise.
EXAMPLES:
sage: Word().is_subword_of(Word('123'))
True
sage: Word('123').is_subword_of(Word('3211333213233321'))
True
sage: Word('321').is_subword_of(Word('11122212112122133111222332'))
False
Returns True if w is a suffix of other, and False otherwise.
EXAMPLES:
sage: w = Word('0123456789')
sage: y = Word('56789')
sage: y.is_suffix(w)
True
sage: w.is_suffix(y)
False
sage: Word('579').is_suffix(w)
False
sage: Word().is_suffix(y)
True
sage: w.is_suffix(Word())
False
sage: Word().is_suffix(Word())
True
Returns True if w is a suffix of other, and False otherwise.
EXAMPLES:
sage: w = Word('0123456789')
sage: y = Word('56789')
sage: y.is_suffix_of(w)
doctest:1: DeprecationWarning: is_suffix_of is deprecated, use is_suffix instead!
True
sage: w.is_suffix_of(y)
False
sage: Word('579').is_suffix_of(w)
False
sage: Word().is_suffix_of(y)
True
sage: w.is_suffix_of(Word())
False
sage: Word().is_suffix_of(Word())
True
Returns True if self is symmetric (or  -symmetric), and
False otherwise.
-symmetric), and
False otherwise.
A word is symmetric (resp.  -symmetric) if it is the
product of two palindromes (resp.
-symmetric) if it is the
product of two palindromes (resp.  -palindromes). See [1] and [2].
-palindromes). See [1] and [2].
INPUT:
EXAMPLES:
sage: Word('abbabab').is_symmetric()
True
sage: Word('ababa').is_symmetric()
True
sage: Word('aababaabba').is_symmetric()
False
sage: Word('aabbbaababba').is_symmetric()
False
sage: f = WordMorphism('a->b,b->a')
sage: Word('aabbbaababba').is_symmetric(f)
True
REFERENCES:
Returns the iterated left ( -)palindromic closure of self.
-)palindromic closure of self.
INPUT:
OUTPUT:
word – the left iterated f-palindromic closure of self.
EXAMPLES:
sage: Word('123').iterated_left_palindromic_closure()
word: 3231323
sage: f = WordMorphism('a->b,b->a')
sage: Word('ab').iterated_left_palindromic_closure(f=f)
word: abbaab
sage: Word('aab').iterated_left_palindromic_closure(f=f)
word: abbaabbaab
TESTS:
If f is not a involution:
sage: f = WordMorphism('a->b,b->b')
sage: Word('aab').iterated_left_palindromic_closure(f=f)
...
ValueError: f must be an involution
REFERENCES:
Returns the iterated ( -)palindromic closure of self.
-)palindromic closure of self.
INPUT:
OUTPUT:
word – If f is None, the right iterated palindromic closure of self; otherwise, the right iterated f-palindromic closure of self. If side is ‘left’, the left palindromic closure.
EXAMPLES:
sage: Word('123').iterated_palindromic_closure()
doctest:1: DeprecationWarning: iterated_palindromic_closure is deprecated, use iterated_left_palindromic_closure or iterated_right_palindromic_closure instead!
word: 1213121
sage: Word('123').iterated_palindromic_closure(side='left')
word: 3231323
sage: Word('1').iterated_palindromic_closure()
word: 1
sage: Word().iterated_palindromic_closure()
word:
sage: Word = Words('ab')
sage: f = WordMorphism('a->b,b->a')
sage: Word('ab').iterated_palindromic_closure(f=f)
word: abbaab
sage: Word('ab').iterated_palindromic_closure(f=f, side='left')
word: abbaab
sage: Word('aab').iterated_palindromic_closure(f=f)
word: ababbaabab
sage: Word('aab').iterated_palindromic_closure(f=f, side='left')
word: abbaabbaab
TESTS:
sage: Word('aab').iterated_palindromic_closure(f=f, side='leftt')
...
ValueError: side must be either 'left' or 'right' (not leftt)
REFERENCES:
Returns the list of all the lacunas of self.
A lacuna is a position in a word where the longest palindromic suffix is not unioccurrent (see [1]).
INPUT:
OUTPUT:
list – list of all the lacunas of self.
EXAMPLES:
sage: w = Word([0,1,1,2,3,4,5,1,13,3])
sage: w.lacunas()
[7, 9]
sage: words.ThueMorseWord()[:100].lacunas()
[8, 9, 24, 25, 32, 33, 34, 35, 36, 37, 38, 39, 96, 97, 98, 99]
sage: f = WordMorphism({0:[1],1:[0]})
sage: words.ThueMorseWord()[:50].lacunas(f)
[0, 2, 4, 12, 16, 17, 18, 19, 48, 49]
REFERENCES:
Returns a dictionary that contains the last position of each letter in self.
EXAMPLES:
sage: Word('1231232').last_position_dict()
{'1': 3, '3': 5, '2': 6}
Returns a dictionary that contains the last position of each letter in self.
EXAMPLES:
sage: Word('1231232').last_position_table()
doctest:1: DeprecationWarning: last_position_table is deprecated, use last_position_dict instead!
{'1': 3, '3': 5, '2': 6}
Returns the length of self.
TESTS:
sage: from sage.combinat.words.word import Word_class
sage: w = Word(iter('abba'*40), length="finite")
sage: w._len is None
True
sage: w.length()
160
sage: w = Word(iter('abba'), length=4)
sage: w._len
4
sage: w.length()
4
sage: def f(n):
... return range(2,12,2)[n]
sage: w = Word(f, length=5)
sage: w.length()
5
Returns the length of the border of self.
The border of a word is the longest word that is both a proper prefix and a proper suffix of self.
EXAMPLES:
sage: Word('121').length_border()
1
sage: Word('1').length_border()
0
sage: Word('1212').length_border()
2
sage: Word('111').length_border()
2
sage: Word().length_border() is None
True
Returns the list of the length of the longest palindromic suffix (lps) for each non-empty prefix of self.
It corresponds to the function 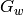 defined in [1].
defined in [1].
INPUT:
OUTPUT:
- list – list of the length of the longest palindromic
- suffix (lps) for each non-empty prefix of self.
EXAMPLES:
sage: Word().lengths_lps()
[]
sage: Word('a').lengths_lps()
[1]
sage: Word('aaa').lengths_lps()
[1, 2, 3]
sage: Word('abbabaabbaab').lengths_lps()
[1, 1, 2, 4, 3, 3, 2, 4, 2, 4, 6, 8]
sage: f = WordMorphism('a->b,b->a')
sage: Word('abbabaabbaab').lengths_lps(f)
[0, 2, 0, 2, 2, 4, 6, 8, 4, 6, 4, 6]
sage: f = WordMorphism({5:[8],8:[5]})
sage: Word([5,8,5,5,8,8,5,5,8,8,5,8,5]).lengths_lps(f)
[0, 2, 2, 0, 2, 4, 6, 4, 6, 8, 10, 12, 4]
REFERENCES:
Returns the list of the lengths of the unioccurrent longest palindromic suffixes (lps) for each non-empty prefix of self. No unioccurrent lps are indicated by None.
It corresponds to the function 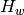 defined in [1] and [2].
defined in [1] and [2].
INPUT:
OUTPUT:
- list – list of the length of the unioccurrent longest palindromic
- suffix (lps) for each non-empty prefix of self. No unioccurrent lps are indicated by None.
EXAMPLES:
sage: w = Word([0,1,1,2,3,4,5,1,13,3])
sage: w.lengths_unioccurrent_lps()
[1, 1, 2, 1, 1, 1, 1, None, 1, None]
sage: f = words.FibonacciWord()[:20]
sage: f.lengths_unioccurrent_lps() == f.lengths_lps()
True
sage: t = words.ThueMorseWord()
sage: t[:20].lengths_unioccurrent_lps()
[1, 1, 2, 4, 3, 3, 2, 4, None, None, 6, 8, 10, 12, 14, 16, 6, 8, 10, 12]
sage: f = WordMorphism({1:[0],0:[1]})
sage: t[:15].lengths_unioccurrent_lps(f)
[None, 2, None, 2, None, 4, 6, 8, 4, 6, 4, 6, None, 4, 6]
REFERENCES:
Return a list of the letters that appear in self, listed in the order of first appearance.
EXAMPLES:
sage: Word([0,1,1,0,1,0,0,1]).letters()
[0, 1]
sage: Word("cacao").letters()
['c', 'a', 'o']
Returns the longest common suffix of self and other.
EXAMPLES:
sage: w = Word('112345678')
sage: u = Word('1115678')
sage: w.longest_common_suffix(u)
word: 5678
sage: u.longest_common_suffix(u)
word: 1115678
sage: u.longest_common_suffix(w)
word: 5678
sage: w.longest_common_suffix(w)
word: 112345678
sage: y = Word('549332345')
sage: w.longest_common_suffix(y)
word:
TESTS:
With the empty word:
sage: w.longest_common_suffix(Word())
word:
sage: Word().longest_common_suffix(w)
word:
sage: Word().longest_common_suffix(Word())
word:
With an infinite word:
sage: t=words.ThueMorseWord('ab')
sage: w.longest_common_suffix(t)
...
TypeError: other must be a finite word
Returns the longest palindromic (or  -palindromic) suffix of self.
-palindromic) suffix of self.
INPUT:
OUTPUT:
- word – If f is None, the longest palindromic suffix of self;
- otherwise, the longest f-palindromic suffix of self.
EXAMPLES:
sage: Word('0111').lps()
word: 111
sage: Word('011101').lps()
word: 101
sage: Word('6667').lps()
word: 7
sage: Word('abbabaab').lps()
word: baab
sage: Word().lps()
word:
sage: f = WordMorphism('a->b,b->a')
sage: Word('abbabaab').lps(f=f)
word: abbabaab
sage: w = Word('33412321')
sage: w.lps(l=3)
word: 12321
sage: Y = Word
sage: w = Y('01101001')
sage: w.lps(l=2)
word: 1001
sage: w.lps()
word: 1001
sage: w.lps(l=None)
word: 1001
sage: Y().lps(l=2)
...
IndexError: list index out of range
sage: v = Word('abbabaab')
sage: pal = v[:0]
sage: for i in range(1, v.length()+1):
... pal = v[:i].lps(l=pal.length())
... print pal
...
word: a
word: b
word: bb
word: abba
word: bab
word: aba
word: aa
word: baab
sage: f = WordMorphism('a->b,b->a')
sage: v = Word('abbabaab')
sage: pal = v[:0]
sage: for i in range(1, v.length()+1):
... pal = v[:i].lps(f=f, l=pal.length())
... print pal
...
word:
word: ab
word:
word: ba
word: ab
word: baba
word: bbabaa
word: abbabaab
Returns the Lyndon factorization of self.
The Lyndon factorization of a finite word  is the unique
factorization of
is the unique
factorization of  as a non-increasing product of Lyndon words,
i.e.,
as a non-increasing product of Lyndon words,
i.e., 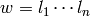 where each
where each 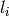 is a Lyndon word and
is a Lyndon word and
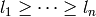 . See for instance [1].
. See for instance [1].
OUTPUT:
list – the list of factors obtained
EXAMPLES:
sage: Word('010010010001000').lyndon_factorization()
(01, 001, 001, 0001, 0, 0, 0)
sage: Words('10')('010010010001000').lyndon_factorization()
(0, 10010010001000)
sage: Word('abbababbaababba').lyndon_factorization()
(abb, ababb, aababb, a)
sage: Words('ba')('abbababbaababba').lyndon_factorization()
(a, bbababbaaba, bba)
sage: Word([1,2,1,3,1,2,1]).lyndon_factorization()
(1213, 12, 1)
TESTS:
sage: Words('01')('').lyndon_factorization()
()
sage: Word('01').lyndon_factorization()
(01)
sage: Words('10')('01').lyndon_factorization()
(0, 1)
sage: lynfac = Word('abbababbaababba').lyndon_factorization()
sage: [x.is_lyndon() for x in lynfac]
[True, True, True, True]
sage: lynfac = Words('ba')('abbababbaababba').lyndon_factorization()
sage: [x.is_lyndon() for x in lynfac]
[True, True, True]
sage: w = words.ThueMorseWord()[:1000]
sage: w == prod(w.lyndon_factorization())
True
REFERENCES:
Returns the period of self.
Let  be an alphabet. An integer
be an alphabet. An integer 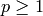 is a period of a
word
is a period of a
word 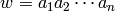 where
where 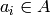 if
if 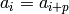 for
for
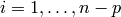 . The smallest period of
. The smallest period of  is called the
period of
is called the
period of  . See Chapter 1 of [1].
. See Chapter 1 of [1].
EXAMPLES:
sage: Word('aba').minimal_period()
2
sage: Word('abab').minimal_period()
2
sage: Word('ababa').minimal_period()
2
sage: Word('ababaa').minimal_period()
5
sage: Word('ababac').minimal_period()
6
sage: Word('aaaaaa').minimal_period()
1
sage: Word('a').minimal_period()
1
sage: Word().minimal_period()
1
REFERENCES:
Returns the number of times self appears as a factor in other.
EXAMPLES:
sage: Word().nb_factor_occurrences_in(Word('123'))
...
NotImplementedError: undefined value
sage: Word('123').nb_factor_occurrences_in(Word('112332312313112332121123'))
4
sage: Word('321').nb_factor_occurrences_in(Word('11233231231311233221123'))
0
Returns the number of times self appears in other as a subword.
EXAMPLES:
sage: Word().nb_subword_occurrences_in(Word('123'))
...
NotImplementedError: undefined value
sage: Word('123').nb_subword_occurrences_in(Word('1133432311132311112'))
11
sage: Word('4321').nb_subword_occurrences_in(Word('1132231112233212342231112'))
0
sage: Word('3').nb_subword_occurrences_in(Word('122332112321213'))
4
Counts the number of distinct factors of self.
INPUT:
OUTPUT:
If n is an integer, returns the number of distinct factors of length n. If n is None, returns the total number of distinct factors.
EXAMPLES:
sage: w = Word([1,2,1,2,3])
sage: w.number_of_factors()
13
sage: map(w.number_of_factors, range(6))
[1, 3, 3, 3, 2, 1]
sage: w = words.ThueMorseWord()[:100]
sage: [w.number_of_factors(i) for i in range(10)]
[1, 2, 4, 6, 10, 12, 16, 20, 22, 24]
sage: Word('1213121').number_of_factors()
22
sage: Word('1213121').number_of_factors(1)
3
sage: Word('a'*100).number_of_factors()
101
sage: Word('a'*100).number_of_factors(77)
1
sage: Word().number_of_factors()
1
sage: Word().number_of_factors(17)
0
sage: blueberry = Word("blueberry")
sage: blueberry.number_of_factors()
43
sage: map(blueberry.number_of_factors, range(10))
[1, 6, 8, 7, 6, 5, 4, 3, 2, 1]
Returns the order of self.
Let 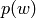 be the period of a word
be the period of a word  . The positive rational number
. The positive rational number
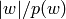 is the order of
is the order of  . See Chapter 8 of [1].
. See Chapter 8 of [1].
OUTPUT:
rational – the order
EXAMPLES:
sage: Word('abaaba').order()
2
sage: Word('ababaaba').order()
8/5
sage: Word('a').order()
1
sage: Word('aa').order()
2
sage: Word().order()
0
REFERENCES:
Returns the partition of the alphabet induced by the overlap of self and other with the given delay.
The partition of the alphabet is given by the equivalence
relation obtained from the symmetric, reflexive and transitive
closure of the set of pairs of letters
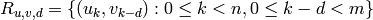 where
where 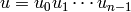 ,
, 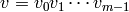 are
two words on the alphabet
are
two words on the alphabet  and
and  is an integer.
is an integer.
The equivalence relation defined by  is inspired from [1].
is inspired from [1].
INPUT:
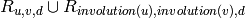 is considered.
is considered.OUTPUT:
EXAMPLES:
sage: W = Words(list('abc')+range(6))
sage: u = W('abc')
sage: v = W(range(5))
sage: u.overlap_partition(v)
{{0, 'a'}, {1, 'b'}, {2, 'c'}, {3}, {4}, {5}}
sage: u.overlap_partition(v, 2)
{{'a'}, {'b'}, {0, 'c'}, {1}, {2}, {3}, {4}, {5}}
sage: u.overlap_partition(v, -1)
{{0}, {1, 'a'}, {2, 'b'}, {3, 'c'}, {4}, {5}}
You can re-use the same disjoint set and do more than one overlap:
sage: p = u.overlap_partition(v, 2)
sage: p
{{'a'}, {'b'}, {0, 'c'}, {1}, {2}, {3}, {4}, {5}}
sage: u.overlap_partition(v, 1, p)
{{'a'}, {0, 1, 'b', 'c'}, {2}, {3}, {4}, {5}}
The function overlap_partition can be used to study equations
on words. For example, if a word  overlaps itself with delay
overlaps itself with delay  , then
, then
 is a period of
is a period of  :
:
sage: W = Words(range(20))
sage: w = W(range(14)); w
word: 0,1,2,3,4,5,6,7,8,9,10,11,12,13
sage: d = 5
sage: p = w.overlap_partition(w, d)
sage: m = WordMorphism(p.element_to_root_dict())
sage: w2 = m(w); w2
word: 56789567895678
sage: w2.minimal_period() == d
True
If a word is equal to its reversal, then it is a palindrome:
sage: W = Words(range(20))
sage: w = W(range(17)); w
word: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16
sage: p = w.overlap_partition(w.reversal(), 0)
sage: m = WordMorphism(p.element_to_root_dict())
sage: w2 = m(w); w2
word: 01234567876543210
sage: w2.parent()
Words over Ordered Alphabet [0, 1, 2, 3, 4, 5, 6, 7, 8, 17, 18, 19]
sage: w2.is_palindrome()
True
If the reversal of a word  is factor of its square
is factor of its square 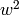 , then
, then
 is symmetric, i.e. the product of two palindromes:
is symmetric, i.e. the product of two palindromes:
sage: W = Words(range(10))
sage: w = W(range(10)); w
word: 0123456789
sage: p = (w*w).overlap_partition(w.reversal(), 4)
sage: m = WordMorphism(p.element_to_root_dict())
sage: w2 = m(w); w2
word: 0110456654
sage: w2.is_symmetric()
True
If the image of the reversal of a word  under an involution
under an involution  is factor of its square
is factor of its square 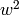 , then
, then  is
is  -symmetric:
-symmetric:
sage: W = Words([-11,-9,..,11])
sage: w = W([1,3,..,11])
sage: w
word: 1,3,5,7,9,11
sage: inv = lambda x:-x
sage: f = WordMorphism(dict( (a, inv(a)) for a in W.alphabet()))
sage: p = (w*w).overlap_partition(f(w).reversal(), 2, involution=f)
sage: m = WordMorphism(p.element_to_root_dict())
sage: m(w)
word: 1,-1,5,7,-7,-5
sage: m(w).is_symmetric(f)
True
TESTS:
sage: W = Words('abcdef')
sage: w = W('abc')
sage: y = W('def')
sage: w.overlap_partition(y, -3)
{{'a'}, {'b'}, {'c'}, {'d'}, {'e'}, {'f'}}
sage: w.overlap_partition(y, -2)
{{'a', 'f'}, {'b'}, {'c'}, {'d'}, {'e'}}
sage: w.overlap_partition(y, -1)
{{'a', 'e'}, {'b', 'f'}, {'c'}, {'d'}}
sage: w.overlap_partition(y, 0)
{{'a', 'd'}, {'b', 'e'}, {'c', 'f'}}
sage: w.overlap_partition(y, 1)
{{'a'}, {'b', 'd'}, {'c', 'e'}, {'f'}}
sage: w.overlap_partition(y, 2)
{{'a'}, {'b'}, {'c', 'd'}, {'e'}, {'f'}}
sage: w.overlap_partition(y, 3)
{{'a'}, {'b'}, {'c'}, {'d'}, {'e'}, {'f'}}
sage: w.overlap_partition(y, 4)
{{'a'}, {'b'}, {'c'}, {'d'}, {'e'}, {'f'}}
sage: W = Words(range(2))
sage: w = W([0,1,0,1,0,1]); w
word: 010101
sage: w.overlap_partition(w, 0)
{{0}, {1}}
sage: w.overlap_partition(w, 1)
{{0, 1}}
sage: empty = Word()
sage: empty.overlap_partition(empty, 'yo')
...
TypeError: delay (=yo) must be an integer
sage: empty.overlap_partition(empty,2,'yo')
...
TypeError: p(=yo) is not a DisjointSet
The involution input can be any callable:
sage: w = Words([-5,..,5])([-5..5])
sage: inv = lambda x:-x
sage: w.overlap_partition(w, 2, involution=inv)
{{-4, -2, 0, 2, 4}, {-5, -3, -1, 1, 3, 5}}
REFERENCES:
 -palindromes,
Mémoire de maîtrise en Mathématiques, Montréal, UQAM, 2008,
109 pages.
-palindromes,
Mémoire de maîtrise en Mathématiques, Montréal, UQAM, 2008,
109 pages.Returns a list of all palindrome prefixes of self.
OUTPUT:
list – A list of all palindrome prefixes of self.
EXAMPLES:
sage: w = Word('abaaba')
sage: w.palindrome_prefixes()
[word: , word: a, word: aba, word: abaaba]
sage: w = Word('abbbbbbbbbb')
sage: w.palindrome_prefixes()
[word: , word: a]
Returns the set of all palindromic (or  -palindromic) factors of self.
-palindromic) factors of self.
INPUT:
OUTPUT:
- set – If f is None, the set of all palindromic factors of self;
- otherwise, the set of all f-palindromic factors of self.
EXAMPLES:
sage: sorted(Word('01101001').palindromes())
[word: , word: 0, word: 00, word: 010, word: 0110, word: 1, word: 1001, word: 101, word: 11]
sage: sorted(Word('00000').palindromes())
[word: , word: 0, word: 00, word: 000, word: 0000, word: 00000]
sage: sorted(Word('0').palindromes())
[word: , word: 0]
sage: sorted(Word('').palindromes())
[word: ]
sage: sorted(Word().palindromes())
[word: ]
sage: f = WordMorphism('a->b,b->a')
sage: sorted(Word('abbabaab').palindromes(f))
[word: , word: ab, word: abbabaab, word: ba, word: baba, word: bbabaa]
Returns the shortest palindrome having self as a prefix (or as a suffix if side==’left’).
See [1].
INPUT:
OUTPUT:
- word – If f is None, the right palindromic closure of self;
- otherwise, the right f-palindromic closure of self. If side is ‘left’, the left palindromic closure.
EXAMPLES:
sage: Word('1233').palindromic_closure()
word: 123321
sage: Word('12332').palindromic_closure()
word: 123321
sage: Word('0110343').palindromic_closure()
word: 01103430110
sage: Word('0110343').palindromic_closure(side='left')
word: 3430110343
sage: Word('01105678').palindromic_closure(side='left')
word: 876501105678
sage: w = Word('abbaba')
sage: w.palindromic_closure()
word: abbababba
sage: f = WordMorphism('a->b,b->a')
sage: w.palindromic_closure(f=f)
word: abbabaab
sage: w.palindromic_closure(f=f, side='left')
word: babaabbaba
TESTS:
sage: f = WordMorphism('a->c,c->a')
sage: w.palindromic_closure(f=f, side='left')
...
KeyError: 'b'
REFERENCES:
Returns interesting statistics about longest ( -)palindromic suffixes
and lacunas of self (see [1] and [2]).
-)palindromic suffixes
and lacunas of self (see [1] and [2]).
Note that a word  has at most
has at most 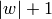 different palindromic factors
(see [3]).
different palindromic factors
(see [3]).
INPUT:
OUTPUT:
EXAMPLES:
sage: a,b,c = Word('abbabaabbaab').palindromic_lacunas_study()
sage: a
[1, 1, 2, 4, 3, 3, 2, 4, 2, 4, 6, 8]
sage: b
[8, 9]
sage: c # random order
set([word: , word: b, word: bab, word: abba, word: bb, word: aa, word: baabbaab, word: baab, word: aba, word: aabbaa, word: a])
sage: f = WordMorphism('a->b,b->a')
sage: a,b,c = Word('abbabaab').palindromic_lacunas_study(f=f)
sage: a
[0, 2, 0, 2, 2, 4, 6, 8]
sage: b
[0, 2, 4]
sage: c # random order
set([word: , word: ba, word: baba, word: ab, word: bbabaa, word: abbabaab])
sage: c == set([Word(), Word('ba'), Word('baba'), Word('ab'), Word('bbabaa'), Word('abbabaab')])
True
REFERENCES:
Returns the Parikh vector of self, i.e., the vector containing the number of occurrences of each letter, given in the order of the alphabet.
See also evaluation_dict.
INPUT:
EXAMPLES:
sage: Words('ab')().parikh_vector()
[0, 0]
sage: Word('aabaa').parikh_vector('abc')
[4, 1, 0]
sage: Word('a').parikh_vector('abc')
[1, 0, 0]
sage: Word('a').parikh_vector('cab')
[0, 1, 0]
sage: Word('a').parikh_vector('bca')
[0, 0, 1]
sage: Word().parikh_vector('ab')
[0, 0]
sage: Word().parikh_vector('abc')
[0, 0, 0]
sage: Word().parikh_vector('abcd')
[0, 0, 0, 0]
TESTS:
sage: Word('aabaa').parikh_vector()
...
TypeError: the alphabet is infinite; specify a finite alphabet or use evaluation_dict() instead
Applies the phi function to self and returns the result. This is the word obtained by taking the first letter of the words obtained by iterating delta on self.
OUTPUT:
word – the result of the phi function
EXAMPLES:
sage: W = Words([1, 2])
sage: W([2,2,1,1,2,1,2,2,1,2,2,1,1,2]).phi()
word: 222222
sage: W([2,1,2,2,1,2,2,1,2,1]).phi()
word: 212113
sage: W().phi()
word:
sage: Word([2,1,2,2,1,2,2,1,2,1]).phi()
word: 212113
sage: Word([2,3,1,1,2,1,2,3,1,2,2,3,1,2]).phi()
word: 21215
sage: Word("aabbabaabaabba").phi()
word: a22222
sage: w = Word([2,3,1,1,2,1,2,3,1,2,2,3,1,2])
REFERENCES:
Apply the inverse of the phi function to self.
INPUT:
OUTPUT:
word – the inverse of the phi function
EXAMPLES:
sage: W = Words([1, 2])
sage: W([2, 2, 2, 2, 1, 2]).phi_inv()
word: 22112122
sage: W([2, 2, 2]).phi_inv(Words([2, 3]))
word: 2233
Returns a vector containing the length of the proper prefix-suffixes for all the non-empty prefixes of self.
EXAMPLES:
sage: Word('121321').prefix_function_table()
[0, 0, 1, 0, 0, 1]
sage: Word('1241245').prefix_function_table()
[0, 0, 0, 1, 2, 3, 0]
sage: Word().prefix_function_table()
[]
Returns the primitive of self.
EXAMPLES:
sage: Word('12312').primitive()
word: 12312
sage: Word('121212').primitive()
word: 12
Returns the length of the primitive of self.
EXAMPLES:
sage: Word('1231').primitive_length()
4
sage: Word('121212').primitive_length()
2
Returns the quasiperiods of self as a list ordered from shortest to longest.
Let  be a finite or infinite word. A quasiperiod of
be a finite or infinite word. A quasiperiod of  is a
proper factor
is a
proper factor  of
of  such that the occurrences of
such that the occurrences of  in
in  entirely cover
entirely cover  , i.e., every position of
, i.e., every position of  falls within some
occurrence of
falls within some
occurrence of  in
in  . See for instance [1], [2], and [3].
. See for instance [1], [2], and [3].
EXAMPLES:
sage: Word('abaababaabaababaaba').quasiperiods()
[word: aba, word: abaaba, word: abaababaaba]
sage: Word('abaaba').quasiperiods()
[word: aba]
sage: Word('abacaba').quasiperiods()
[]
REFERENCES:
Returns the Rauzy graph of the factors of length n of self.
The vertices are the factors of length  and there is an edge from
and there is an edge from
 to
to  if
if 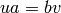 is a factor of length
is a factor of length 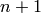 for some letters
for some letters
 and
and  .
.
INPUT:
EXAMPLES:
sage: w = Word(range(10)); w
word: 0123456789
sage: g = w.rauzy_graph(3); g
Looped digraph on 8 vertices
sage: WordOptions(identifier='')
sage: g.vertices()
[012, 123, 234, 345, 456, 567, 678, 789]
sage: g.edges()
[(012, 123, 3),
(123, 234, 4),
(234, 345, 5),
(345, 456, 6),
(456, 567, 7),
(567, 678, 8),
(678, 789, 9)]
sage: WordOptions(identifier='word: ')
sage: f = words.FibonacciWord()[:100]
sage: f.rauzy_graph(8)
Looped digraph on 9 vertices
sage: w = Word('1111111')
sage: g = w.rauzy_graph(3)
sage: g.edges()
[(word: 111, word: 111, word: 1)]
sage: w = Word('111')
sage: for i in range(5) : w.rauzy_graph(i)
Looped multi-digraph on 1 vertex
Looped digraph on 1 vertex
Looped digraph on 1 vertex
Looped digraph on 1 vertex
Looped digraph on 0 vertices
Multi-edges are allowed for the empty word:
sage: W = Words('abcde')
sage: w = W('abc')
sage: w.rauzy_graph(0)
Looped multi-digraph on 1 vertex
sage: _.edges()
[(word: , word: , word: a),
(word: , word: , word: b),
(word: , word: , word: c)]
Returns the reduced Rauzy graph of order  of self.
of self.
INPUT:
 is a factor of length
is a factor of length  of self.
of self.OUTPUT:
Looped multi-digraph
DEFINITION:
For infinite periodic words (resp. for finite words of type ![u^i
u[0:j]](../../../_images/math/9e47946858a360d82949e13f19b88ce212f7bdac.png) ), the reduced Rauzy graph of order
), the reduced Rauzy graph of order  (resp. for
(resp. for  smaller or equal to
smaller or equal to 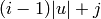 ) is the directed graph whose
unique vertex is the prefix
) is the directed graph whose
unique vertex is the prefix  of length
of length  of self and which has
an only edge which is a loop on
of self and which has
an only edge which is a loop on  labelled by
labelled by ![w[n+1:|w|] p](../../../_images/math/d23f48a83709af682fbf98df334cae9c4c5cec38.png) where
where  is the unique return word to
is the unique return word to  .
.
In other cases, it is the directed graph defined as followed. Let
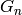 be the Rauzy graph of order
be the Rauzy graph of order  of self. The vertices are the
vertices of
of self. The vertices are the
vertices of 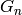 that are either special or not prolongable to the
right or to the left. For each couple (
that are either special or not prolongable to the
right or to the left. For each couple ( ,
,  ) of such vertices
and each directed path in
) of such vertices
and each directed path in 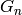 from
from  to
to  that contains no
other vertices that are special, there is an edge from
that contains no
other vertices that are special, there is an edge from  to
to  in the reduced Rauzy graph of order
in the reduced Rauzy graph of order  whose label is the label of
the path in
whose label is the label of
the path in 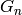 .
.
Note
In the case of infinite recurrent non periodic words, this definition correspond to the following one that can be found in [1] and [2] where a simple path is a path that begins with a special factor, ends with a special factor and contains no other vertices that are special:
The reduced Rauzy graph of factors of length  is obtained
from
is obtained
from 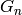 by replacing each simple path
by replacing each simple path 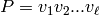 with an edge
with an edge 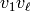 whose label is the
concatenation of the labels of the edges of
whose label is the
concatenation of the labels of the edges of  .
.
EXAMPLES:
sage: w = Word(range(10)); w
word: 0123456789
sage: g = w.reduced_rauzy_graph(3); g
Looped multi-digraph on 2 vertices
sage: g.vertices()
[word: 012, word: 789]
sage: g.edges()
[(word: 012, word: 789, word: 3456789)]
For the Fibonacci word:
sage: f = words.FibonacciWord()[:100]
sage: g = f.reduced_rauzy_graph(8);g
Looped multi-digraph on 2 vertices
sage: g.vertices()
[word: 01001010, word: 01010010]
sage: g.edges()
[(word: 01001010, word: 01010010, word: 010), (word: 01010010, word: 01001010, word: 01010), (word: 01010010, word: 01001010, word: 10)]
For periodic words:
sage: from itertools import cycle
sage: w = Word(cycle('abcd'))[:100]
sage: g = w.reduced_rauzy_graph(3)
sage: g.edges()
[(word: abc, word: abc, word: dabc)]
sage: w = Word('111')
sage: for i in range(5) : w.reduced_rauzy_graph(i)
Looped digraph on 1 vertex
Looped digraph on 1 vertex
Looped digraph on 1 vertex
Looped multi-digraph on 1 vertex
Looped multi-digraph on 0 vertices
For ultimately periodic words:
sage: sigma = WordMorphism('a->abcd,b->cd,c->cd,d->cd')
sage: w = sigma.fixed_point('a')[:100]; w
word: abcdcdcdcdcdcdcdcdcdcdcdcdcdcdcdcdcdcdcd...
sage: g = w.reduced_rauzy_graph(5)
sage: g.vertices()
[word: abcdc, word: cdcdc]
sage: g.edges()
[(word: abcdc, word: cdcdc, word: dc), (word: cdcdc, word: cdcdc, word: dc)]
AUTHOR:
Julien Leroy (March 2010): initial version
REFERENCES:
Returns the set of return words of fact in self.
This is the set of all factors starting by the given factor and ending just before the next occurrence of this factor. See [1] and [2].
EXAMPLES:
sage: Word('21331233213231').return_words(Word('2'))
set([word: 213, word: 21331, word: 233])
sage: Word().return_words(Word('213'))
set([])
sage: Word('121212').return_words(Word('1212'))
set([word: 12])
REFERENCES:
Returns the word generated by mapping a letter to each occurrence of the return words for the given factor dropping any dangling prefix and suffix. See for instance [1].
EXAMPLES:
sage: Word('12131221312313122').return_words_derivate(Word('1'))
word: 123242
REFERENCES:
Returns True if the word self is reverse lexicographically less than other.
EXAMPLES:
sage: Word([1,2,4]).rev_lex_less(Word([1,3,2]))
True
sage: Word([3,2,1]).rev_lex_less(Word([1,2,3]))
False
Returns the reversal of self.
EXAMPLES:
sage: Word('124563').reversal()
word: 365421
Returns the index of the last occurrence of sub in self, such that sub is contained within self[start:end]. Returns -1 on failure.
INPUT:
OUTPUT:
non negative integer or -1
EXAMPLES:
sage: w = Word([0,1,0,0,1])
sage: w.rfind(Word([0,1]))
3
sage: w.rfind(Word([0,1]), end=4)
0
sage: w.rfind(Word([0,1]), end=5)
3
sage: w.rfind(Word([0,0]), start=2, end=5)
2
sage: w.rfind(Word([0,0]), start=3, end=5) == -1
True
Instances of Word_str handle string inputs as well:
sage: w = Word('abac')
sage: w.rfind('a')
2
sage: w.rfind(Word('a'))
2
Returns the combinatorial class representing the shifted shuffle product between words self and other. This is the same as the shuffle product of self with the word obtained from other by incrementing its values (i.e. its letters) by the given shift.
INPUT:
OUTPUT:
Combinatorial class of shifted shuffle products of self and other.
EXAMPLES:
sage: w = Word([0,1,1])
sage: sp = w.shifted_shuffle(w); sp
Shuffle product of word: 011 and word: 344
sage: sp = w.shifted_shuffle(w, 2); sp
Shuffle product of word: 011 and word: 233
sage: sp.cardinality()
20
sage: WordOptions(identifier='')
sage: sp.list()
[011233, 012133, 012313, 012331, 021133, 021313, 021331, 023113, 023131, 023311, 201133, 201313, 201331, 203113, 203131, 203311, 230113, 230131, 230311, 233011]
sage: WordOptions(identifier='word: ')
sage: y = Word('aba')
sage: y.shifted_shuffle(w,2)
...
ValueError: for shifted shuffle, words must only contain integers as letters
Returns the combinatorial class representing the shuffle product between words self and other. This consists of all words of length self.length()+other.length() that have both self and other as subwords.
If overlap is non-zero, then the combinatorial class representing the shuffle product with overlaps is returned. The calculation of the shift in each overlap is done relative to the order of the alphabet. For example, “a” shifted by “a” is “b” in the alphabet [a, b, c] and 0 shifted by 1 in [0, 1, 2, 3] is 2.
INPUT:
OUTPUT:
Combinatorial class of shuffle product of self and other
EXAMPLES:
sage: ab = Word("ab")
sage: cd = Word("cd")
sage: sp = ab.shuffle(cd); sp
Shuffle product of word: ab and word: cd
sage: sp.cardinality()
6
sage: sp.list()
[word: abcd, word: acbd, word: acdb, word: cabd, word: cadb, word: cdab]
sage: w = Word([0,1])
sage: u = Word([2,3])
sage: w.shuffle(w)
Shuffle product of word: 01 and word: 01
sage: u.shuffle(u)
Shuffle product of word: 23 and word: 23
sage: w.shuffle(u)
Shuffle product of word: 01 and word: 23
sage: w.shuffle(u,2)
Overlapping shuffle product of word: 01 and word: 23 with 2 overlaps
EXAMPLES:
sage: w = Word('abaccefa')
sage: w.size_of_alphabet()
doctest:1: DeprecationWarning: size_of_alphabet() is deprecated, use parent().size_of_alphabet() instead!
+Infinity
sage: y = Words('456')('64654564')
sage: y.size_of_alphabet()
3
Returns the standard factorization of self.
The standard factorization of a word  is the unique
factorization:
is the unique
factorization: 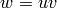 where
where  is the longest proper suffix
of
is the longest proper suffix
of  that is a Lyndon word.
that is a Lyndon word.
Note that if  is a Lyndon word with standard factorization
is a Lyndon word with standard factorization
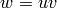 , then
, then  and
and  are also Lyndon words and
are also Lyndon words and 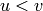 .
.
See for instance [1] and [2].
OUTPUT:
list – the list of factors
EXAMPLES:
sage: Words('01')('0010110011').standard_factorization()
(001011, 0011)
sage: Words('123')('1223312').standard_factorization()
(12233, 12)
sage: Word([3,2,1]).standard_factorization()
(32, 1)
sage: Words('123')('').standard_factorization()
()
sage: w = Word('0010110011',alphabet='01')
sage: w.standard_factorization()
(001011, 0011)
sage: w = Word('0010110011',alphabet='10')
sage: w.standard_factorization()
(001011001, 1)
sage: w = Word('1223312',alphabet='123')
sage: w.standard_factorization()
(12233, 12)
REFERENCES:
Returns the standard factorization of the Lyndon factorization of self.
OUTPUT:
list of lists – the factorization
EXAMPLES:
sage: Words('123')('1221131122').standard_factorization_of_lyndon_factorization()
[(12, 2), (1, 13), (1, 122)]
Returns the standard permutation of the word self on the ordered alphabet. It is defined as the permutation with exactly the same number of inversions as w. Equivalently, it is the permutation of minimal length whose inverse sorts self.
EXAMPLES:
sage: w = Word([1,2,3,2,2,1]); w
word: 123221
sage: p = w.standard_permutation(); p
[1, 3, 6, 4, 5, 2]
sage: v = Word(p.inverse().action(w)); v
word: 112223
sage: Permutations(w.length()).filter( \
... lambda q: q.length() <= p.length() and \
... q.inverse().action(w) == list(v) ).list()
[[1, 3, 6, 4, 5, 2]]
sage: w = Words([1,2,3])([1,2,3,2,2,1,2,1]); w
word: 12322121
sage: p = w.standard_permutation(); p
[1, 4, 8, 5, 6, 2, 7, 3]
sage: Word(p.inverse().action(w))
word: 11122223
sage: w = Words([3,2,1])([1,2,3,2,2,1,2,1]); w
word: 12322121
sage: p = w.standard_permutation(); p
[6, 2, 1, 3, 4, 7, 5, 8]
sage: Word(p.inverse().action(w))
word: 32222111
sage: w = Words('ab')('abbaba'); w
word: abbaba
sage: p = w.standard_permutation(); p
[1, 4, 5, 2, 6, 3]
sage: Word(p.inverse().action(w))
word: aaabbb
sage: w = Words('ba')('abbaba'); w
word: abbaba
sage: p = w.standard_permutation(); p
[4, 1, 2, 5, 3, 6]
sage: Word(p.inverse().action(w))
word: bbbaaa
Alias for implicit_suffix_tree().
EXAMPLES:
sage: Word('abbabaab').suffix_tree()
Implicit Suffix Tree of the word: abbabaab
Returns the suffix trie of self.
The suffix trie of a finite word  is a data structure
representing the factors of
is a data structure
representing the factors of  . It is a tree whose edges are
labelled with letters of
. It is a tree whose edges are
labelled with letters of  , and whose leafs correspond to
suffixes of
, and whose leafs correspond to
suffixes of  .
.
See sage.combinat.words.suffix_trees.SuffixTrie? for more information.
EXAMPLES:
sage: w = Word("cacao")
sage: w.suffix_trie()
Suffix Trie of the word: cacao
sage: w = Word([0,1,0,1,1])
sage: w.suffix_trie()
Suffix Trie of the word: 01011
Returns the word w with entries at positions i and j swapped. By default, j = i+1.
EXAMPLES:
sage: Word([1,2,3]).swap(0,2)
word: 321
sage: Word([1,2,3]).swap(1)
word: 132
sage: Word("abba").swap(1,-1)
word: aabb
Returns the word with positions i and i+1 exchanged if self[i] < self[i+1]. Otherwise, it returns self.
EXAMPLES:
sage: w = Word([1,3,2])
sage: w.swap_decrease(0)
word: 312
sage: w.swap_decrease(1)
word: 132
sage: w.swap_decrease(1) is w
True
sage: Words("ab")("abba").swap_decrease(0)
word: baba
sage: Words("ba")("abba").swap_decrease(0)
word: abba
Returns the word with positions i and i+1 exchanged if self[i] > self[i+1]. Otherwise, it returns self.
EXAMPLES:
sage: w = Word([1,3,2])
sage: w.swap_increase(1)
word: 123
sage: w.swap_increase(0)
word: 132
sage: w.swap_increase(0) is w
True
sage: Words("ab")("abba").swap_increase(0)
word: abba
sage: Words("ba")("abba").swap_increase(0)
word: baba
Returns a list of integers from [0,1,...,self.length()-1] in the same relative order as the letters in self in the parent.
EXAMPLES:
sage: from itertools import count
sage: w = Word('abbabaab')
sage: w.to_integer_list()
[0, 1, 1, 0, 1, 0, 0, 1]
sage: w = Word(iter("cacao"), length="finite")
sage: w.to_integer_list()
[1, 0, 1, 0, 2]
sage: w = Words([3,2,1])([2,3,3,1])
sage: w.to_integer_list()
[1, 0, 0, 2]
Returns a word defined over the integers [0,1,...,self.length()-1] whose letters are in the same relative order in the parent.
EXAMPLES:
sage: from itertools import count
sage: w = Word('abbabaab')
sage: w.to_integer_word()
word: 01101001
sage: w = Word(iter("cacao"), length="finite")
sage: w.to_integer_word()
word: 10102
sage: w = Words([3,2,1])([2,3,3,1])
sage: w.to_integer_word()
word: 1002