Functions that compute some of the sequences in Sloane’s tables
EXAMPLES:
Type sloane.[tab] to see a list of the sequences that are defined.
sage: a = sloane.A000005; a
The integer sequence tau(n), which is the number of divisors of n.
sage: a(1)
1
sage: a(6)
4
sage: a(100)
9
Type d._eval?? to see how the function that
computes an individual term of the sequence is implemented.
The input must be a positive integer:
sage: a(0)
...
ValueError: input n (=0) must be a positive integer
sage: a(1/3)
...
TypeError: input must be an int, long, or Integer
You can also change how a sequence prints:
sage: a = sloane.A000005; a
The integer sequence tau(n), which is the number of divisors of n.
sage: a.rename('(..., tau(n), ...)')
sage: a
(..., tau(n), ...)
sage: a.reset_name()
sage: a
The integer sequence tau(n), which is the number of divisors of n.
TESTS:
sage: a = sloane.A000001;
sage: a == loads(dumps(a))
True
AUTHORS:
- William Stein: framework
- Jaap Spies: most sequences
- Nick Alexander: updated framework
-
class sage.combinat.sloane_functions.A000001
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000004
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000005
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000007
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000008
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000009
Bases: sage.combinat.sloane_functions.SloaneSequence
-
cf()
EXAMPLES:
sage: it = sloane.A000009.cf()
sage: [it.next() for i in range(14)]
[1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, 12, 15, 18]
-
list(n)
EXAMPLES:
sage: sloane.A000009.list(14)
[1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, 12, 15, 18]
-
class sage.combinat.sloane_functions.A000010
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000012
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000015
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000016
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000027
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000030
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000032
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000035
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000040
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000041
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000043
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000045
Bases: sage.combinat.sloane_functions.SloaneSequence
-
fib()
Returns a generator over all Fibonacci numbers, starting with 0.
EXAMPLES:
sage: it = sloane.A000045.fib()
sage: [it.next() for i in range(10)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
-
list(n)
EXAMPLES:
sage: sloane.A000045.list(10)
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
-
class sage.combinat.sloane_functions.A000069
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000073
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A000073.list(10)
[0, 0, 1, 1, 2, 4, 7, 13, 24, 44]
-
class sage.combinat.sloane_functions.A000079
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000085
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000100
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000108
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000110
- Bases: sage.combinat.sloane_functions.ExponentialNumbers
-
class sage.combinat.sloane_functions.A000120
Bases: sage.combinat.sloane_functions.SloaneSequence
-
f(n)
EXAMPLES:
sage: [sloane.A000120.f(n) for n in range(10)]
[0, 1, 1, 2, 1, 2, 2, 3, 1, 2]
-
class sage.combinat.sloane_functions.A000124
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000129
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A000142
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000153
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence
-
class sage.combinat.sloane_functions.A000165
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000166
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000169
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000203
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000204
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000213
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A000213.list(10)
[1, 1, 1, 3, 5, 9, 17, 31, 57, 105]
-
class sage.combinat.sloane_functions.A000217
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000225
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000244
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000255
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence
-
class sage.combinat.sloane_functions.A000261
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence
-
class sage.combinat.sloane_functions.A000272
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000290
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000292
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000302
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000312
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000326
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000330
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000396
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000578
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000583
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000587
- Bases: sage.combinat.sloane_functions.ExponentialNumbers
-
class sage.combinat.sloane_functions.A000668
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000670
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000720
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A000796
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A000796.list(10)
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]
-
pi()
Based on an algorithm of Lambert Meertens The ABC-programming
language!!!
EXAMPLES:
sage: it = sloane.A000796.pi()
sage: [it.next() for i in range(10)]
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]
-
class sage.combinat.sloane_functions.A000961
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A000961.list(10)
[1, 2, 3, 4, 5, 7, 8, 9, 11, 13]
-
class sage.combinat.sloane_functions.A000984
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001006
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001045
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A001055
Bases: sage.combinat.sloane_functions.SloaneSequence
-
nwf(n, m)
EXAMPLES:
sage: sloane.A001055.nwf(4,1)
0
sage: sloane.A001055.nwf(4,2)
1
sage: sloane.A001055.nwf(4,3)
1
sage: sloane.A001055.nwf(4,4)
2
-
class sage.combinat.sloane_functions.A001109
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A001110
Bases: sage.combinat.sloane_functions.RecurrenceSequence
-
g(k)
EXAMPLES:
sage: sloane.A001110.g(2)
2
sage: sloane.A001110.g(1)
0
-
class sage.combinat.sloane_functions.A001147
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001157
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001189
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001221
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001222
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001227
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001333
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A001358
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A001358.list(9)
[4, 6, 9, 10, 14, 15, 21, 22, 25]
-
class sage.combinat.sloane_functions.A001405
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001477
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A001694
Bases: sage.combinat.sloane_functions.SloaneSequence
-
is_powerful(n)
This function returns True if and only if  is a Powerful
Number:
is a Powerful
Number:
A positive integer  is powerful if for every prime
is powerful if for every prime
 dividing
dividing  ,
, 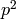 also divides
also divides
 . See Sloane’s OEIS A001694.
. See Sloane’s OEIS A001694.
INPUT:
OUTPUT:
- True - if
 is a Powerful number, else
False
is a Powerful number, else
False
EXAMPLES:
sage: a = sloane.A001694
sage: a.is_powerful(2500)
True
sage: a.is_powerful(20)
False
AUTHORS:
-
list(n)
EXAMPLES:
sage: sloane.A001694.list(9)
[1, 4, 8, 9, 16, 25, 27, 32, 36]
-
class sage.combinat.sloane_functions.A001836
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A001836.list(9)
[53, 83, 158, 263, 293, 368, 578, 683, 743]
-
class sage.combinat.sloane_functions.A001906
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A001909
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence
-
class sage.combinat.sloane_functions.A001910
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence
-
class sage.combinat.sloane_functions.A001969
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A002110
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A002113
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A002113.list(15)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55]
-
class sage.combinat.sloane_functions.A002275
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A002378
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A002620
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A002808
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A002808.list(10)
[4, 6, 8, 9, 10, 12, 14, 15, 16, 18]
-
class sage.combinat.sloane_functions.A003418
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A004086
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A004526
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A005100
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A005100.list(10)
[1, 2, 3, 4, 5, 7, 8, 9, 10, 11]
-
class sage.combinat.sloane_functions.A005101
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A005101.list(10)
[12, 18, 20, 24, 30, 36, 40, 42, 48, 54]
-
class sage.combinat.sloane_functions.A005117
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A005117.list(10)
[1, 2, 3, 5, 6, 7, 10, 11, 13, 14]
-
class sage.combinat.sloane_functions.A005408
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A005843
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A006318
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A006530
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A006882
Bases: sage.combinat.sloane_functions.SloaneSequence
-
df()
Double factorials n!!: a(n)=n*a(n-2).
EXAMPLES:
sage: it = sloane.A006882.df()
sage: [it.next() for i in range(10)]
[1, 1, 2, 3, 8, 15, 48, 105, 384, 945]
-
list(n)
EXAMPLES:
sage: sloane.A006882.list(10)
[1, 1, 2, 3, 8, 15, 48, 105, 384, 945]
-
class sage.combinat.sloane_functions.A007318
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A008275
Bases: sage.combinat.sloane_functions.SloaneSequence
-
s(n, k)
EXAMPLES:
sage: sloane.A008275.s(4,2)
11
sage: sloane.A008275.s(5,2)
-50
sage: sloane.A008275.s(5,3)
35
-
class sage.combinat.sloane_functions.A008277
Bases: sage.combinat.sloane_functions.SloaneSequence
-
s2(n, k)
Returns the Stirling number S2(n,k) of the 2nd kind.
EXAMPLES:
sage: sloane.A008277.s2(4,2)
7
-
class sage.combinat.sloane_functions.A008683
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A010060
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A015521
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A015523
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A015530
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A015531
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A015551
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A018252
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A020639
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A020639.list(10)
[1, 2, 3, 2, 5, 2, 7, 2, 3, 2]
-
class sage.combinat.sloane_functions.A046660(offset=1)
Bases: sage.combinat.sloane_functions.SloaneSequence
Excess of  = number of prime divisors (with
multiplicity) - number of prime divisors (without multiplicity).
= number of prime divisors (with
multiplicity) - number of prime divisors (without multiplicity).
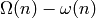 .
.
INPUT:
OUTPUT:
EXAMPLES:
sage: a = sloane.A046660; a
Excess of n = Bigomega (with multiplicity) - omega (without multiplicity).
sage: a(0)
...
ValueError: input n (=0) must be a positive integer
sage: a(1)
0
sage: a(8)
2
sage: a(41)
0
sage: a(84792)
2
sage: a.list(12)
[0, 0, 0, 1, 0, 0, 0, 2, 1, 0, 0, 1]
AUTHORS:
-
class sage.combinat.sloane_functions.A049310
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A051959
Bases: sage.combinat.sloane_functions.RecurrenceSequence
-
g(k)
EXAMPLES:
sage: sloane.A051959.g(2)
15
sage: sloane.A051959.g(1)
0
-
class sage.combinat.sloane_functions.A055790
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence2
-
class sage.combinat.sloane_functions.A061084
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A064553
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A079922(offset=1)
Bases: sage.combinat.sloane_functions.SloaneSequence
function returns solutions to the Dancing School problem with
 girls and
girls and 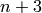 boys.
boys.
The value is 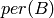 , the permanent of the (0,1)-matrix
, the permanent of the (0,1)-matrix
 of size
of size 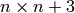 with
with 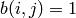 if and only if
if and only if 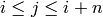 .
.
REFERENCES:
- Jaap Spies, Nieuw Archief voor Wiskunde, 5/7 nr 4, December 2006
INPUT:
OUTPUT:
EXAMPLES:
sage: a = sloane.A079922; a
Solutions to the Dancing School problem with n girls and n+3 boys
sage: a.offset
1
sage: a(1)
4
sage: a(8)
2227
sage: a.list(8)
[4, 13, 36, 90, 212, 478, 1044, 2227]
Compare: Searching Sloane’s online database... Solution to the
Dancing School Problem with n girls and n+3 boys: f(n,3). [4, 13,
36, 90, 212, 478, 1044, 2227]
sage: a(-1)
...
ValueError: input n (=-1) must be a positive integer
AUTHORS:
-
class sage.combinat.sloane_functions.A079923(offset=1)
Bases: sage.combinat.sloane_functions.SloaneSequence
function returns solutions to the Dancing School problem with
 girls and
girls and 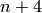 boys.
boys.
The value is 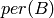 , the permanent of the (0,1)-matrix
, the permanent of the (0,1)-matrix
 of size
of size 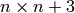 with
with 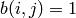 if and only if
if and only if 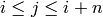 .
.
REFERENCES:
- Jaap Spies, Nieuw Archief voor Wiskunde, 5/7 nr 4,
December 2006
INPUT:
OUTPUT:
EXAMPLES:
sage: a = sloane.A079923; a
Solutions to the Dancing School problem with n girls and n+4 boys
sage: a.offset
1
sage: a(1)
5
sage: a(8)
15458
sage: a.list(8)
[5, 21, 76, 246, 738, 2108, 5794, 15458]
Compare: Searching Sloane’s online database... Solution to the
Dancing School Problem with n girls and n+4 boys: f(n,4). [5, 21,
76, 246, 738, 2108, 5794, 15458]
sage: a(0)
...
ValueError: input n (=0) must be a positive integer
AUTHORS:
-
class sage.combinat.sloane_functions.A082411
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A083103
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A083104
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A083105
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A083216
- Bases: sage.combinat.sloane_functions.RecurrenceSequence2
-
class sage.combinat.sloane_functions.A090010
- Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence2
-
class sage.combinat.sloane_functions.A090012
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A090013
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A090014
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A090015
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A090016
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A111774
Bases: sage.combinat.sloane_functions.SloaneSequence
-
is_number_of_the_third_kind(n)
This function returns True if and only if  is a number
of the third kind.
is a number
of the third kind.
A number is of the third kind if it can be written as a sum of at
least three consecutive positive integers. Odd primes can only be
written as a sum of two consecutive integers. Powers of 2 do not
have a representation as a sum of  consecutive integers
(other than the trivial
consecutive integers
(other than the trivial  for
for 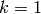 ).
).
See: http://www.jaapspies.nl/mathfiles/problem2005-2C.pdf
INPUT:
OUTPUT:
- True - if n is not prime and not a power of 2
False -
EXAMPLES:
sage: a = sloane.A111774
sage: a.is_number_of_the_third_kind(6)
True
sage: a.is_number_of_the_third_kind(100)
True
sage: a.is_number_of_the_third_kind(16)
False
sage: a.is_number_of_the_third_kind(97)
False
AUTHORS:
-
list(n)
EXAMPLES:
sage: sloane.A111774.list(12)
[6, 9, 10, 12, 14, 15, 18, 20, 21, 22, 24, 25]
-
class sage.combinat.sloane_functions.A111775
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A111776
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.A111787
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.ExponentialNumbers(a)
- Bases: sage.combinat.sloane_functions.SloaneSequence
-
class sage.combinat.sloane_functions.ExtremesOfPermanentsSequence(offset=1)
Bases: sage.combinat.sloane_functions.SloaneSequence
-
gen(a0, a1, d)
EXAMPLES:
sage: it = sloane.A000153.gen(0,1,2)
sage: [it.next() for i in range(5)]
[0, 1, 2, 7, 32]
-
list(n)
EXAMPLES:
sage: sloane.A000153.list(8)
[0, 1, 2, 7, 32, 181, 1214, 9403]
-
class sage.combinat.sloane_functions.ExtremesOfPermanentsSequence2(offset=1)
Bases: sage.combinat.sloane_functions.ExtremesOfPermanentsSequence
-
gen(a0, a1, d)
EXAMPLES:
sage: from sage.combinat.sloane_functions import ExtremesOfPermanentsSequence2
sage: e = ExtremesOfPermanentsSequence2()
sage: it = e.gen(6,43,6)
sage: [it.next() for i in range(5)]
[6, 43, 307, 2542, 23799]
-
class sage.combinat.sloane_functions.RecurrenceSequence(offset=1)
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A001110.list(8)
[0, 1, 36, 1225, 41616, 1413721, 48024900, 1631432881]
-
class sage.combinat.sloane_functions.RecurrenceSequence2(offset=1)
Bases: sage.combinat.sloane_functions.SloaneSequence
-
list(n)
EXAMPLES:
sage: sloane.A001906.list(10)
[0, 1, 3, 8, 21, 55, 144, 377, 987, 2584]
-
class sage.combinat.sloane_functions.Sloane
Bases: sage.structure.sage_object.SageObject
A collection of Sloane generating functions.
This class inspects sage.combinat.sloane_functions, accumulating
all the SloaneSequence classes starting with ‘A’. These are listed
for tab completion, but not instantiated until requested.
EXAMPLES: Ensure we have lots of entries:
sage: len(sloane.trait_names()) > 100
True
And ensure none are being incorrectly returned:
sage: [ None for n in sloane.trait_names() if not n.startswith('A') ]
[]
Ensure we can access dynamic constructions and cache correctly:
sage: s = sloane.A000587
sage: s is sloane.A000587
True
And that we can access other functions in parent classes:
sage: sloane.__class__
<class 'sage.combinat.sloane_functions.Sloane'>
AUTHORS:
-
trait_names()
List Sloane generating functions for tab-completion.
The member classes are inspected from module
sage.combinat.sloane_functions.
They must be sub classes of SloaneSequence and must start with ‘A’.
These restrictions are only to prevent typos, incorrect inspecting,
etc.
EXAMPLES:
sage: type(sloane.trait_names())
<type 'list'>
-
class sage.combinat.sloane_functions.SloaneSequence(offset=1)
Bases: sage.structure.sage_object.SageObject
Base class for a Sloane integer sequence.
EXAMPLES:
We create a dummy sequence:
-
list(n)
Return n terms of the sequence: sequence[offset], sequence[offset+1], ... , sequence[offset+n-1].
EXAMPLES:
sage: sloane.A000012.list(4)
[1, 1, 1, 1]
-
sage.combinat.sloane_functions.perm_mh(m, h)
This functions calculates 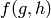 from Sloane’s sequences
A079908-A079928
from Sloane’s sequences
A079908-A079928
INPUT:
- m - positive integer
- h - non negative integer
OUTPUT: permanent of the m x (m+h) matrix, etc.
EXAMPLES:
sage: from sage.combinat.sloane_functions import perm_mh
sage: perm_mh(3,3)
36
sage: perm_mh(3,4)
76
AUTHORS:
-
sage.combinat.sloane_functions.recur_gen2(a0, a1, a2, a3)
homogeneous general second-order linear recurrence generator with
fixed coefficients
a(0) = a0, a(1) = a1, a(n) = a2*a(n-1) + a3*a(n-2)
EXAMPLES:
sage: from sage.combinat.sloane_functions import recur_gen2
sage: it = recur_gen2(1,1,1,1)
sage: [it.next() for i in range(10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
-
sage.combinat.sloane_functions.recur_gen2b(a0, a1, a2, a3, b)
inhomogenous second-order linear recurrence generator with fixed
coefficients and 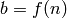
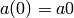 ,
, 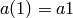 ,
,
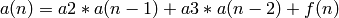 .
.
EXAMPLES:
sage: from sage.combinat.sloane_functions import recur_gen2b
sage: it = recur_gen2b(1,1,1,1, lambda n: 0)
sage: [it.next() for i in range(10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
-
sage.combinat.sloane_functions.recur_gen3(a0, a1, a2, a3, a4, a5)
homogeneous general third-order linear recurrence generator with
fixed coefficients
a(0) = a0, a(1) = a1, a(2) = a2, a(n) = a3*a(n-1) + a4*a(n-2) +
a5*a(n-3)
EXAMPLES:
sage: from sage.combinat.sloane_functions import recur_gen3
sage: it = recur_gen3(1,1,1,1,1,1)
sage: [it.next() for i in range(10)]
[1, 1, 1, 3, 5, 9, 17, 31, 57, 105]

 is a Powerful
Number:
is a Powerful
Number: is powerful if for every prime
is powerful if for every prime
 dividing
dividing  ,
, 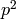 also divides
also divides
 . See Sloane’s OEIS A001694.
. See Sloane’s OEIS A001694. is a Powerful number, else
False
is a Powerful number, else
False = number of prime divisors (with
multiplicity) - number of prime divisors (without multiplicity).
= number of prime divisors (with
multiplicity) - number of prime divisors (without multiplicity).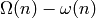 .
. girls and
girls and 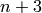 boys.
boys.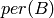 , the permanent of the (0,1)-matrix
, the permanent of the (0,1)-matrix
 of size
of size 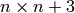 with
with 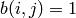 if and only if
if and only if 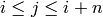 .
. girls and
girls and 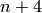 boys.
boys.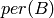 , the permanent of the (0,1)-matrix
, the permanent of the (0,1)-matrix
 of size
of size 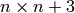 with
with 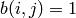 if and only if
if and only if 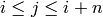 .
. is a number
of the third kind.
is a number
of the third kind. consecutive integers
(other than the trivial
consecutive integers
(other than the trivial  for
for 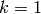 ).
).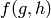 from Sloane’s sequences
A079908-A079928
from Sloane’s sequences
A079908-A079928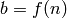
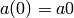 ,
, 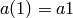 ,
,
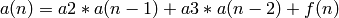 .
.