Compute Bell and Uppuluri-Carpenter numbers.

AUTHORS:

• Nick Alexander

sage.combinat.expnums.clear_mpz_globals()

sage.combinat.expnums.expnums(n, aa)

Compute the first exponential numbers around 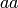, starting with the zero-th.

INPUT:

• n - C machine int
• aa - C machine int

OUTPUT: A list of length .

ALGORITHM: We use the same integer addition algorithm as GAP. This is an extension of Bell’s triangle to the general case of exponential numbers. The recursion performs 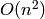additions, but the running time is dominated by the cost of the last integer addition, because the growth of the integer results of partial computations is exponential in . The algorithm stores integers, but each is exponential in .

EXAMPLES:

sage: expnums(10, 1)
[1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147]

sage: expnums(10, -1)
[1, -1, 0, 1, 1, -2, -9, -9, 50, 267]

sage: expnums(1, 1)
[1]
sage: expnums(0, 1)
[]
sage: expnums(-1, 0)
[]

AUTHORS:

• Nick Alexander

sage.combinat.expnums.expnums2(n, aa)

A vanilla python (but compiled via Cython) implementation of expnums.

We Compute the first exponential numbers around 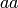, starting with the zero-th.

EXAMPLES:

sage: from sage.combinat.expnums import expnums2
sage: expnums2(10, 1)
[1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147]

sage.combinat.expnums.gmp_randrange(n1, n2)

sage.combinat.expnums.init_mpz_globals()