LLT Polynomials

sage.combinat.sf.llt.LLT(R, k, t=None)

Returns a class for working with LLT polynomials.

EXAMPLES:

sage: L3 = LLT(QQ,3); L3
LLT polynomials at level 3 over Fraction Field of Univariate Polynomial Ring in t over Rational Field
sage: L3.cospin([3,2,1])
(t+1)*m[1, 1] + m[2]
sage: L3.hcospin()
LLT polynomials in the HCosp basis at level 3 with t=t over Fraction Field of Univariate Polynomial Ring in t over Rational Field

sage.combinat.sf.llt.LLTHCospin(R, level, t=None)

Returns the LLT polynomials in the HCospin basis at level level.

EXAMPLES:

sage: HCosp3 = LLTHCospin(QQ,3)
sage: HCosp3([1])^2
1/t*HCosp3[1, 1] + ((t-1)/t)*HCosp3[2]

sage: s = SFASchur(HCosp3.base_ring())
sage: HCosp3(s([2]))
HCosp3[2]
sage: HCosp3(s([1,1]))
1/t*HCosp3[1, 1] - 1/t*HCosp3[2]

sage.combinat.sf.llt.LLTHSpin(R, level, t=None)

Returns the LLT polynomials in the HSpin basis at level level.

EXAMPLES:

sage: HSp3 = LLTHSpin(QQ,3)
sage: HSp3([1])^2
HSp[1, 1] + (-t+1)*HSp[2]

sage: s = SFASchur(HSp3.base_ring())
sage: HSp3(s([2]))
HSp[2]
sage: HSp3(s([1,1]))
HSp[1, 1] - t*HSp[2]

class sage.combinat.sf.llt.LLT_class(R, k, t=None)

base_ring()

Returns the base ring of self.

EXAMPLES:

sage: LLT(QQ,3).base_ring()
Fraction Field of Univariate Polynomial Ring in t over Rational Field

cospin(skp)

EXAMPLES:

sage: L3 = LLT(QQ,3)
sage: L3.cospin([2,1])
m[1]
sage: L3.cospin([3,2,1])
(t+1)*m[1, 1] + m[2]
sage: s = SFASchur(L3.base_ring())
sage: s(L3.cospin([[2],[1],[2]]))
t^4*s[2, 2, 1] + t^3*s[3, 1, 1] + (t^3+t^2)*s[3, 2] + (t^2+t)*s[4, 1] + s[5]

hcospin()

Returns the HCopsin basis.

EXAMPLES:

sage: LLT(QQ,3).hcospin()
LLT polynomials in the HCosp basis at level 3 with t=t over Fraction Field of Univariate Polynomial Ring in t over Rational Field

hspin()

Returns the HSpin basis.

EXAMPLES:

sage: LLT(QQ,3).hspin()
LLT polynomials in the HSp basis at level 3 with t=t over Fraction Field of Univariate Polynomial Ring in t over Rational Field

level()

Returns the level of self.

EXAMPLES:

sage: LLT(QQ,3).level()
3

spin_square(skp)

Returns the spin polynomial associated with skp with the substitution 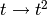made.

EXAMPLES:

sage: L3 = LLT(QQ,3)
sage: L3.spin_square([2,1])
t*m[1]
sage: L3.spin_square([3,2,1])
(t^3+t)*m[1, 1] + t^3*m[2]
sage: L3.spin_square([[1],[1],[1]])
(t^6+2*t^4+2*t^2+1)*m[1, 1, 1] + (t^6+t^4+t^2)*m[2, 1] + t^6*m[3]

class sage.combinat.sf.llt.LLT_cospin(R, level, t=None)

Bases: sage.combinat.sf.llt.LLT_generic

class Element(M, x)

Bases: sage.combinat.sf.llt.LLT_generic.Element

class sage.combinat.sf.llt.LLT_generic(R, level, t=None)

Bases: sage.combinat.sf.sfa.SymmetricFunctionAlgebra_generic

class Element(M, x)

Bases: sage.combinat.sf.sfa.SymmetricFunctionAlgebra_generic_Element

LLT_generic.level()

Returns the level of self.

EXAMPLES:

sage: from sage.combinat.sf.llt import *
sage: HSp3 = LLT_spin(QQ, 3)
sage: HSp3.level()
3

class sage.combinat.sf.llt.LLT_spin(R, level, t=None)

Bases: sage.combinat.sf.llt.LLT_generic

class Element(M, x)

Bases: sage.combinat.sf.llt.LLT_generic.Element