Macdonald Polynomials¶

sage.combinat.sf.macdonald.MacdonaldPolynomialsH(R, q=None, t=None)¶

Returns the Macdonald polynomials on the H basis. When the H basis is expanded on the Schur basis, the coefficients are the qt-Kostka numbers.

EXAMPLES:

sage: H = MacdonaldPolynomialsH(QQ)
sage: s = SFASchur(H.base_ring())
sage: s(H([2]))
q*s[1, 1] + s[2]
sage: s(H([1,1]))
s[1, 1] + t*s[2]

Coercions to/from the Schur basis are implemented:

sage: H = MacdonaldPolynomialsH(QQ)
sage: s = SFASchur(H.base_ring())
sage: H(s([2]))
((-q)/(-q*t+1))*McdH[1, 1] + (1/(-q*t+1))*McdH[2]

sage.combinat.sf.macdonald.MacdonaldPolynomialsHt(R, q=None, t=None)¶

Returns the Macdonald polynomials on the Ht basis. The elements of the Ht basis are eigenvectors of the nabla operator. When expanded on the Schur basis, the coefficients are the modified qt-Kostka numbers.

EXAMPLES:

sage: Ht = MacdonaldPolynomialsHt(QQ)
sage: [Ht(p).nabla() for p in Partitions(3)]
[q^3*McdHt[3], q*t*McdHt[2, 1], t^3*McdHt[1, 1, 1]]

sage: s = SFASchur(Ht.base_ring())
sage: from sage.combinat.sf.macdonald import qt_kostka
sage: q,t = Ht.base_ring().gens()
sage: s(Ht([2,1]))
q*t*s[1, 1, 1] + (q+t)*s[2, 1] + s[3]
sage: qt_kostka([1,1,1],[2,1]).subs(t=1/t)*t^Partition([2,1]).weighted_size()
q*t
sage: qt_kostka([2,1],[2,1]).subs(t=1/t)*t^Partition([2,1]).weighted_size()
q + t
sage: qt_kostka([3],[2,1]).subs(t=1/t)*t^Partition([2,1]).weighted_size()
1

Coercions to/from the Schur basis are implemented:

sage: Ht = MacdonaldPolynomialsHt(QQ)
sage: s = SFASchur(Ht.base_ring())
sage: Ht(s([2,1]))
((-q)/(-q*t^2+t^3+q^2-q*t))*McdHt[1, 1, 1] + ((q^2+q*t+t^2)/(-q^2*t^2+q^3+t^3-q*t))*McdHt[2, 1] + ((-t)/(q^3-q^2*t-q*t+t^2))*McdHt[3]
sage: Ht(s([2]))
((-q)/(-q+t))*McdHt[1, 1] + (t/(-q+t))*McdHt[2]

sage.combinat.sf.macdonald.MacdonaldPolynomialsJ(R, q=None, t=None)¶

Returns the Macdonald polynomials on the J basis also known as the integral form of the Macdonald polynomials. These are scalar multiples of both the P and Q bases. When expressed in the P or Q basis, the scaling coefficients are polynomials in q and t rather than rational functions.

EXAMPLES:

sage: J = MacdonaldPolynomialsJ(QQ); J
Macdonald polynomials in the J basis over Fraction Field of Multivariate Polynomial Ring in q, t over Rational Field
sage: P = MacdonaldPolynomialsP(QQ)
sage: Q = MacdonaldPolynomialsQ(QQ)
sage: P(J([2]))
(q*t^2-q*t-t+1)*McdP[2]
sage: P(J([1,1]))
(t^3-t^2-t+1)*McdP[1, 1]
sage: Q(J([2]))
(q^3-q^2-q+1)*McdQ[2]
sage: Q(J([1,1]))
(q^2*t-q*t-q+1)*McdQ[1, 1]

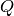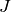Coercions from the $Q$ and $J$ basis (proportional) and to/from the Schur basis are implemented:

sage: P = MacdonaldPolynomialsP(QQ)
sage: Q = MacdonaldPolynomialsQ(QQ)
sage: J = MacdonaldPolynomialsJ(QQ)
sage: s = SFASchur(P.base_ring())

sage: J(P([2]))
(1/(q*t^2-q*t-t+1))*McdJ[2]

sage: J(Q([2]))
(1/(q^3-q^2-q+1))*McdJ[2]

sage: s(J([2]))
(-q*t+t^2+q-t)*s[1, 1] + (q*t^2-q*t-t+1)*s[2]
sage: J(s([2]))
((q-t)/(q*t^4-q*t^3-q*t^2-t^3+q*t+t^2+t-1))*McdJ[1, 1] + (1/(q*t^2-q*t-t+1))*McdJ[2]

sage.combinat.sf.macdonald.MacdonaldPolynomialsP(R, q=None, t=None)¶

Returns the Macdonald polynomials on the P basis. These are upper triangularly related to the monomial symmetric functions and are orthogonal with respect to the qt-Hall scalar product.

EXAMPLES:

sage: P = MacdonaldPolynomialsP(QQ); P
Macdonald polynomials in the P basis over Fraction Field of Multivariate Polynomial Ring in q, t over Rational Field
sage: m = SFAMonomial(P.base_ring())
sage: P.transition_matrix(m,2)
[                          1 (q*t - q + t - 1)/(q*t - 1)]
[                          0                           1]
sage: P([1,1]).scalar_qt(P([2]))
0
sage: P([2]).scalar_qt(P([2]))
(q^3 - q^2 - q + 1)/(q*t^2 - q*t - t + 1)
sage: P([1,1]).scalar_qt(P([1,1]))
(q^2*t - q*t - q + 1)/(t^3 - t^2 - t + 1)

When q = 0, the Macdonald polynomials on the P basis are the same as the Hall-Littlewood polynomials on the P basis.

sage: P = MacdonaldPolynomialsP(QQ,q=0)
sage: P([2])^2
(t+1)*McdP[2, 2] + (-t+1)*McdP[3, 1] + McdP[4]
sage: HLP = HallLittlewoodP(QQ)
sage: HLP([2])^2
(t+1)*P[2, 2] + (-t+1)*P[3, 1] + P[4]

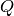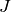Coercions from the $Q$ and $J$ basis (proportional) are implemented:

sage: P = MacdonaldPolynomialsP(QQ)
sage: Q = MacdonaldPolynomialsQ(QQ)
sage: J = MacdonaldPolynomialsJ(QQ)
sage: s = SFASchur(P.base_ring())

sage: P(Q([2]))
((q*t^2-q*t-t+1)/(q^3-q^2-q+1))*McdP[2]
sage: P(Q([2,1]))
((-q*t^4+2*q*t^3-q*t^2+t^2-2*t+1)/(-q^4*t+2*q^3*t-q^2*t+q^2-2*q+1))*McdP[2, 1]

sage: P(J([2]))
(q*t^2-q*t-t+1)*McdP[2]
sage: P(J([2,1]))
(-q*t^4+2*q*t^3-q*t^2+t^2-2*t+1)*McdP[2, 1]

By transitivity, one get coercions from the classical bases:

sage: P(s([2]))
((q-t)/(q*t-1))*McdP[1, 1] + McdP[2]
sage: P(s([2,1]))
((q*t-t^2+q-t)/(q*t^2-1))*McdP[1, 1, 1] + McdP[2, 1]

sage.combinat.sf.macdonald.MacdonaldPolynomialsQ(R, q=None, t=None)¶

Returns the Macdonald polynomials on the Q basis. These are dual to the Macdonald polynomials on the P basis with respect to the qt-Hall scalar product.

EXAMPLES:

sage: Q = MacdonaldPolynomialsQ(QQ); Q
Macdonald polynomials in the Q basis over Fraction Field of Multivariate Polynomial Ring in q, t over Rational Field
sage: P = MacdonaldPolynomialsP(QQ)
sage: Q([2]).scalar_qt(P([2]))
1
sage: Q([2]).scalar_qt(P([1,1]))
0
sage: Q([1,1]).scalar_qt(P([2]))
0
sage: Q([1,1]).scalar_qt(P([1,1]))
1
sage: Q(P([2]))
((q^3-q^2-q+1)/(q*t^2-q*t-t+1))*McdQ[2]
sage: Q(P([1,1]))
((q^2*t-q*t-q+1)/(t^3-t^2-t+1))*McdQ[1, 1]

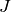Coercions from the $P$ and $J$ basis (proportional) are implemented:

sage: P = MacdonaldPolynomialsP(QQ)
sage: Q = MacdonaldPolynomialsQ(QQ)
sage: J = MacdonaldPolynomialsJ(QQ)
sage: s = SFASchur(P.base_ring())

sage: Q(J([2]))
(q^3-q^2-q+1)*McdQ[2]

sage: Q(P([2]))
((q^3-q^2-q+1)/(q*t^2-q*t-t+1))*McdQ[2]
sage: P(Q(P([2])))
McdP[2]
sage: Q(P(Q([2])))
McdQ[2]

By transitivity, one get coercions from the classical bases:

sage: Q(s([2]))
((q^2-q*t-q+t)/(t^3-t^2-t+1))*McdQ[1, 1] + ((q^3-q^2-q+1)/(q*t^2-q*t-t+1))*McdQ[2]

sage.combinat.sf.macdonald.MacdonaldPolynomialsS(R, q=None, t=None)¶

Returns the modified Schur functions defined by the plethystic substitution $S_{\mu} = s_{\mu}[X(1-t)]$ . When the Macdonald polynomials in the J basis are expressed in terms of the modified Schur functions, the coefficients are qt-Kostka numbers.

EXAMPLES:

sage: S = MacdonaldPolynomialsS(QQ)
sage: J = MacdonaldPolynomialsJ(QQ)
sage: S(J([2]))
q*McdS[1, 1] + McdS[2]
sage: S(J([1,1]))
McdS[1, 1] + t*McdS[2]
sage: from sage.combinat.sf.macdonald import qt_kostka
sage: qt_kostka([2],[1,1])
t
sage: qt_kostka([1,1],[2])
q

Coercions to/from the Schur basis are implemented:

sage: S = MacdonaldPolynomialsS(QQ)
sage: J = MacdonaldPolynomialsJ(QQ)
sage: S(J([2]))
q*McdS[1, 1] + McdS[2]
sage: S(J([1,1]))
McdS[1, 1] + t*McdS[2]

class sage.combinat.sf.macdonald.MacdonaldPolynomials_generic(R, q=None, t=None)¶

Bases: sage.combinat.sf.sfa.SymmetricFunctionAlgebra_generic

class Element(M, x)¶

Bases: sage.combinat.sf.sfa.SymmetricFunctionAlgebra_generic_Element

nabla()¶

Returns the value of the nabla operator applied to self. The eigenvectors of the nabla operator are the Macdonald polynomials in the Ht basis.

EXAMPLES:

sage: from sage.combinat.sf.macdonald import *
sage: P = MacdonaldPolynomialsP(QQ)
sage: P([1,1]).nabla()
((q^2*t+q*t^2-2*t)/(q*t-1))*McdP[1, 1] + McdP[2]

omega_qt()¶

Returns the image of self under the 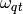$\omega_{qt}$ automorphism.

EXAMPLES:

sage: H = MacdonaldPolynomialsH(QQ)
sage: H([1,1]).omega_qt()
((2*q^2-2*q*t-2*q+2*t)/(t^3-t^2-t+1))*McdH[1, 1] + ((q-1)/(t-1))*McdH[2]

scalar_qt(x)¶

Returns the qt-Hall scalar product of self and x by converting both to the power-sum basis.

EXAMPLES:

sage: H = MacdonaldPolynomialsH(QQ)
sage: H([1]).scalar_qt(H([1]))
(-q + 1)/(-t + 1)

MacdonaldPolynomials_generic.c1(part)¶

Returns the qt-Hall scalar product between J(part) and P(part).

EXAMPLES:

sage: P = MacdonaldPolynomialsP(QQ)
sage: P.c1(Partition([2,1]))
-q^4*t + 2*q^3*t - q^2*t + q^2 - 2*q + 1

MacdonaldPolynomials_generic.c2(part)¶

Returns the qt-Hall scalar product between J(part) and Q(part).

EXAMPLES:

sage: P = MacdonaldPolynomialsP(QQ)
sage: P.c2(Partition([2,1]))
-q*t^4 + 2*q*t^3 - q*t^2 + t^2 - 2*t + 1

class sage.combinat.sf.macdonald.MacdonaldPolynomials_h(R, q=None, t=None)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic

class Element(M, x)¶: Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic.Element

class sage.combinat.sf.macdonald.MacdonaldPolynomials_ht(R, q=None, t=None)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic

class Element(M, x)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic.Element

nabla()¶

Returns the value of the nabla operator applied to self. The eigenvectors of the nabla operator are the Macdonald polynomials in the Ht basis.

EXAMPLES:

sage: Ht = MacdonaldPolynomialsHt(QQ)
sage: t = Ht.t; q = Ht.q;
sage: a = sum(Ht(p) for p in Partitions(3))
sage: a.nabla() == t^3*Ht([1,1,1])+q*t*Ht([2,1]) + q^3*Ht([3])
True

class sage.combinat.sf.macdonald.MacdonaldPolynomials_j(R, q=None, t=None)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic

class Element(M, x)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic.Element

scalar_qt(x)¶

Returns the qt-Hall scalar product of self and x. If x is in the Macdonald J basis, then specialized code is used; otherwise, both are converted to the power-sums and the scalar product is carried out there.

EXAMPLES:

sage: J = MacdonaldPolynomialsJ(QQ)
sage: J([1,1]).scalar_qt(J([1,1]))
q^2*t^4 - q^2*t^3 - q*t^4 - q^2*t^2 + q^2*t + 2*q*t^2 + t^3 - t^2 - q - t + 1
sage: J([1,1]).scalar_qt(J([2]))
0
sage: J([2]).scalar_qt(J([2]))
q^4*t^2 - q^4*t - q^3*t^2 - q^2*t^2 + q^3 + 2*q^2*t + q*t^2 - q^2 - q - t + 1

class sage.combinat.sf.macdonald.MacdonaldPolynomials_p(R, q=None, t=None)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic

class Element(M, x)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic.Element

scalar_qt(x)¶

Returns the qt-Hall scalar product of self and x. If x is in the Macdonald P or Q basis, then specialized code is used; otherwise, both are converted to the power-sums and the scalar product is carried out there.

EXAMPLES:

sage: Q = MacdonaldPolynomialsQ(QQ)
sage: P = MacdonaldPolynomialsP(QQ)
sage: a = P([2])
sage: b = Q([2])
sage: a.scalar_qt(a)
(q^3 - q^2 - q + 1)/(q*t^2 - q*t - t + 1)
sage: a.scalar_qt(b)
1

MacdonaldPolynomials_p.scalar_qt_basis(part1, part2=None)¶

Returns the scalar product of P[part1] and P[part2]

EXAMPLES:: sage: P = MacdonaldPolynomialsP(QQ) sage: P.scalar_qt_basis(Partition([2,1]), Partition([1,1,1])) 0 sage: f = P.scalar_qt_basis(Partition([3,2,1]), Partition([3,2,1])) sage: factor(f.numerator()) (q - 1)^3 * (q^2*t - 1)^2 * (q^3*t^2 - 1) sage: factor(f.denominator()) (t - 1)^3 * (q*t^2 - 1)^2 * (q^2*t^3 - 1)
With a single argument, takes part2 = part1: sage: P.scalar_qt_basis(Partition([2,1]), Partition([2,1])) (-q^4*t + 2*q^3*t - q^2*t + q^2 - 2*q + 1)/(-q*t^4 + 2*q*t^3 - q*t^2 + t^2 - 2*t + 1)

NT: those results do not quite with Macdonald Symmetric Function and Orthogonal Polynomials p.12 (11.3). Is this P basis a normalization variant of that of Macdo?

class sage.combinat.sf.macdonald.MacdonaldPolynomials_q(R, q=None, t=None)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic

class Element(M, x)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic.Element

scalar_qt(x)¶

Returns the qt-Hall scalar product of self and x. If x is in the Macdonald P basis, then specialized code is used; otherwise, both are converted to the power-sums and the scalar product is carried out there.

EXAMPLES:

sage: Q = MacdonaldPolynomialsQ(QQ)
sage: H = MacdonaldPolynomialsH(QQ)
sage: a = Q([2])
sage: a.scalar_qt(a)
(-q*t^2 + q*t + t - 1)/(-q^3 + q^2 + q - 1)
sage: a.scalar_qt(H([1,1]))
t

class sage.combinat.sf.macdonald.MacdonaldPolynomials_s(R, q=None, t=None)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic

class Element(M, x)¶

Bases: sage.combinat.sf.macdonald.MacdonaldPolynomials_generic.Element

creation(k)¶

EXAMPLES:

sage: S = MacdonaldPolynomialsS(QQ)
sage: a = S(1)
sage: a.creation(1)
(-q+1)*McdS[1]
sage: a.creation(2)
(q^2*t-q*t-q+1)*McdS[1, 1] + (q^2-q*t-q+t)*McdS[2]

omega_qt()¶

Returns the image of self under the Frobenius / omega automorphism.

EXAMPLES:

sage: S = MacdonaldPolynomialsS(QQ)
sage: S([1,1]).omega_qt()
(t/(t^3-t^2-t+1))*McdS[1, 1] + ((-1)/(-t^3+t^2+t-1))*McdS[2]

sage.combinat.sf.macdonald.c1(part, q, t)¶

This function returns the qt-Hall scalar product between J(part) and P(part).

EXAMPLES:

sage: from sage.combinat.sf.macdonald import c1
sage: R.<q,t> = QQ[]
sage: c1(Partition([2,1]),q,t)
-q^4*t + 2*q^3*t - q^2*t + q^2 - 2*q + 1
sage: c1(Partition([1,1]),q,t)
q^2*t - q*t - q + 1

sage.combinat.sf.macdonald.c2(part, q, t)¶

This function returns the qt-Hall scalar product between J(part) and Q(part).

EXAMPLES:

sage: from sage.combinat.sf.macdonald import c2
sage: R.<q,t> = QQ[]
sage: c2(Partition([1,1]),q,t)
t^3 - t^2 - t + 1
sage: c2(Partition([2,1]),q,t)
-q*t^4 + 2*q*t^3 - q*t^2 + t^2 - 2*t + 1

sage.combinat.sf.macdonald.qt_kostka(lam, mu)¶

Returns the 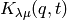$K_{\lambda\mu}(q,t)$ by computing the change of basis from the Macdonald H basis to the Schurs.

EXAMPLES:

sage: from sage.combinat.sf.macdonald import qt_kostka
sage: qt_kostka([2,1,1],[1,1,1,1])
t^3 + t^2 + t
sage: qt_kostka([1,1,1,1],[2,1,1])
q
sage: qt_kostka([1,1,1,1],[3,1])
q^3
sage: qt_kostka([1,1,1,1],[1,1,1,1])
1
sage: qt_kostka([2,1,1],[2,2])
q^2*t + q*t + q
sage: qt_kostka([2,2],[2,2])
q^2*t^2 + 1
sage: qt_kostka([4],[3,1])
t
sage: qt_kostka([2,2],[3,1])
q^2*t + q
sage: qt_kostka([3,1],[2,1,1])
q*t^3 + t^2 + t
sage: qt_kostka([2,1,1],[2,1,1])
q*t^2 + q*t + 1
sage: qt_kostka([2,1],[1,1,1,1])
0

Macdonald Polynomials¶

Previous topic

Next topic

This Page

Navigation

Macdonald Polynomials¶

Previous topic

Next topic

This Page

Quick search

Navigation