k-Schur Functions¶

sage.combinat.sf.kschur.kSchurFunctions(R, k, t=None)¶

Returns the k-Schur functions. See the examples below for caveats on their use.

EXAMPLES:

sage: ks3 = kSchurFunctions(QQ, 3); ks3
k-Schur Functions at level 3 over Univariate Polynomial Ring in t over Rational Field
sage: s = SFASchur(ks3.base_ring()) # Allow 't' coefficients for the Schurs.
sage: t = ks3.t # Allow 't' as input
sage: s(ks3([3,2,1]))
s[3, 2, 1] + t*s[4, 1, 1] + t*s[4, 2] + t^2*s[5, 1]

sage: ks3(s([3, 2, 1]) + t*s([4, 1, 1]) + t*s([4, 2]) + t^2*s([5, 1]))
ks3[3, 2, 1]

k-Schurs are indexed by partitions with first part 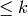$\le k$ . Constructing a k-Schur function for a larger partition raises an error:

sage: ks3([4,3,2,1])  # 
...
TypeError: do not know how to make x (= [4, 3, 2, 1]) an element of self (=k-Schur Functions at level 3 over Univariate Polynomial Ring in t over Rational Field)

Note: this used to return 0 instead. What is preferable?

Similarly, attempting to convert a function that is not in the linear span of the k-Schur’s raises an error:

sage: ks3(s([4]))
...
ValueError: s[4] is not in the space spanned by k-Schur Functions at level 3 over Univariate Polynomial Ring in t over Rational Field.

Note that the product of k-Schurs is not guaranteed to be in the space spanned by the k-Schurs. In general, we only have that a k-Schur times a j-Schur is a (k+j)-Schur. This fact is not currently incorporated into the Sage design, so the multiplication of k-Schur functions may return an error. This example shows how to get around this ‘manually’.

sage: ks2 = kSchurFunctions(QQ, 2)
sage: ks2([2,1])^2
...
ValueError: s[2, 2, 1, 1] + s[2, 2, 2] + s[3, 1, 1, 1] + (2*t+2)*s[3, 2, 1] + (t^2+1)*s[3,
3] + (2*t+1)*s[4, 1, 1] + (t^2+2*t+1)*s[4, 2] + (t^2+2*t)*s[5, 1] + t^2*s[6] is not in the
space spanned by k-Schur Functions at level 2 over Univariate Polynomial Ring in t over
Rational Field.

sage: f = s(ks2([2,1]))^2; f # Convert to Schur functions first and multiply there.
s[2, 2, 1, 1] + s[2, 2, 2] + s[3, 1, 1, 1] + (2*t+2)*s[3, 2, 1] + (t^2+1)*s[3,
3] + (2*t+1)*s[4, 1, 1] + (t^2+2*t+1)*s[4, 2] + (t^2+2*t)*s[5, 1] + t^2*s[6]
sage: ks4 = kSchurFunctions(QQ, 4)
sage: ks4(f) # The product of two 'ks2's is a 'ks4'.
ks4[2, 2, 1, 1] + ks4[2, 2, 2] + ks4[3, 1, 1, 1] + (t+2)*ks4[3, 2, 1] + (t^2+1)*ks4[3, 3] + (t+1)*ks4[4, 1, 1] + ks4[4, 2]

However, at t=1, the product of k-Schurs is in the span of the k-Schurs. Below are some examples at t=1.

sage: ks3 = kSchurFunctions(QQ, 3, 1); ks3
k-Schur Functions at level 3 with t=1 over Rational Field
sage: s = SFASchur(ks3.base_ring())
sage: ks3(s([3]))
ks3[3]
sage: s(ks3([3,2,1]))
s[3, 2, 1] + s[4, 1, 1] + s[4, 2] + s[5, 1]
sage: ks3([2,1])^2
ks3[2, 2, 1, 1] + ks3[2, 2, 2] + ks3[3, 1, 1, 1]