Kostka-Foulkes Polynomials

Based on the algorithms in John Stembridge’s SF package for Maple which can be found at http://www.math.lsa.umich.edu/~jrs/maple.html .

sage.combinat.sf.kfpoly.KostkaFoulkesPolynomial(mu, nu, t=None)

Returns the Kostka-Foulkes polynomial .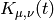

EXAMPLES:

sage: KostkaFoulkesPolynomial([2,2],[2,2])
1
sage: KostkaFoulkesPolynomial([2,2],[4])
0
sage: KostkaFoulkesPolynomial([2,2],[1,1,1,1])
t^4 + t^2
sage: KostkaFoulkesPolynomial([2,2],[2,1,1])
t
sage: q = PolynomialRing(QQ,'q').gen()
sage: KostkaFoulkesPolynomial([2,2],[2,1,1],q)
q

sage.combinat.sf.kfpoly.compat(n, mu, nu)

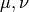Generate all possible partitions of that can precede in a rigging sequence.

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import *
sage: compat(4, [1], [2,1])
[[1, 1, 1, 1], [2, 1, 1], [2, 2], [3, 1], [4]]
sage: compat(3, [1], [2,1])
[[1, 1, 1], [2, 1], [3]]
sage: compat(2, [1], [])
[[2]]
sage: compat(3, [1], [])
[[2, 1], [3]]
sage: compat(3, [2], [1])
[[3]]
sage: compat(4, [1,1], [])
[[2, 2], [3, 1], [4]]
sage: compat(4, [2], [])
[[4]]

sage.combinat.sf.kfpoly.dom(mu, snu)

Returns True if sum(mu[:i+1]) >= snu[i] for all 0 <= i < len(snu); otherwise, it returns False.

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import *
sage: dom([3,2,1],[2,4,5])
True
sage: dom([3,2,1],[2,4,7])
False
sage: dom([3,2,1],[2,6,5])
False
sage: dom([3,2,1],[4,4,4])
False

sage.combinat.sf.kfpoly.kfpoly(mu, nu, t=None)

Returns the Kostka-Foulkes polynomial 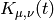by generating all rigging sequences for the shape 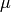, and then selecting those of content .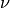

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import kfpoly
sage: kfpoly([2,2], [2,1,1])
t
sage: kfpoly([4], [2,1,1])
t^3
sage: kfpoly([4], [2,2])
t^2
sage: kfpoly([1,1,1,1], [2,2])
0

sage.combinat.sf.kfpoly.q_bin(a, b, t=None)

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import *
sage: t = PolynomialRing(ZZ, 't').gen()        
sage: q_bin(4,2, t)
t^8 + t^7 + 2*t^6 + 2*t^5 + 3*t^4 + 2*t^3 + 2*t^2 + t + 1
sage: q_bin(4,3, t)
t^12 + t^11 + 2*t^10 + 3*t^9 + 4*t^8 + 4*t^7 + 5*t^6 + 4*t^5 + 4*t^4 + 3*t^3 + 2*t^2 + t + 1

sage.combinat.sf.kfpoly.riggings(part)

Generate all possible rigging sequences for a fixed sage.combinat.partition.

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import *
sage: riggings([3])
[[[1, 1, 1]], [[2, 1]], [[3]]]
sage: riggings([2,1])
[[[2, 1], [1]], [[3], [1]]]
sage: riggings([1,1,1])
[[[3], [2], [1]]]
sage: riggings([2,2])
[[[2, 2], [1, 1]], [[3, 1], [1, 1]], [[4], [1, 1]], [[4], [2]]]
sage: riggings([2,2,2])
[[[3, 3], [2, 2], [1, 1]],
 [[4, 2], [2, 2], [1, 1]],
 [[5, 1], [2, 2], [1, 1]],
 [[6], [2, 2], [1, 1]],
 [[5, 1], [3, 1], [1, 1]],
 [[6], [3, 1], [1, 1]],
 [[6], [4], [2]]]

sage.combinat.sf.kfpoly.schur_to_hl(mu, t=None)

Returns a dictionary corresponding to 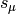in Hall-Littlewood P basis.

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import *    
sage: schur_to_hl([1,1,1])
{[1, 1, 1]: 1}
sage: a = schur_to_hl([2,1])
sage: for m,c in sorted(a.iteritems()): print m, c
[1, 1, 1] t^2 + t
[2, 1] 1
sage: a = schur_to_hl([3])
sage: for m,c in sorted(a.iteritems()): print m, c
[1, 1, 1] t^3
[2, 1] t
[3] 1
sage: a = schur_to_hl([4])
sage: for m,c in sorted(a.iteritems()): print m, c
[1, 1, 1, 1] t^6
[2, 1, 1] t^3
[2, 2] t^2
[3, 1] t
[4] 1
sage: a = schur_to_hl([3,1])
sage: for m,c in sorted(a.iteritems()): print m, c
[1, 1, 1, 1] t^5 + t^4 + t^3
[2, 1, 1] t^2 + t
[2, 2] t
[3, 1] 1
sage: a = schur_to_hl([2,2])
sage: for m,c in sorted(a.iteritems()): print m, c
[1, 1, 1, 1] t^4 + t^2
[2, 1, 1] t
[2, 2] 1
sage: a = schur_to_hl([2,1,1])
sage: for m,c in sorted(a.iteritems()): print m, c        
[1, 1, 1, 1] t^3 + t^2 + t
[2, 1, 1] 1
sage: a = schur_to_hl([1,1,1,1])
sage: for m,c in sorted(a.iteritems()): print m, c   
[1, 1, 1, 1] 1
sage: a = schur_to_hl([2,2,2])
sage: for m,c in sorted(a.iteritems()): print m, c   
[1, 1, 1, 1, 1, 1] t^9 + t^7 + t^6 + t^5 + t^3
[2, 1, 1, 1, 1] t^4 + t^2
[2, 2, 1, 1] t
[2, 2, 2] 1

sage.combinat.sf.kfpoly.weight(rg, t=None)

Returns the weight of a rigging.

EXAMPLES:

sage: from sage.combinat.sf.kfpoly import *
sage: t = PolynomialRing(ZZ, 't').gen()
sage: weight([[2,1], [1]], t)
1
sage: weight([[3],[1]], t)
t^2 + t
sage: weight([[2,1],[3]], t)
t^4
sage: weight([[2, 2], [1, 1]],t)
1
sage: weight([[3, 1], [1, 1]],t)
t
sage: weight([[4], [1, 1]],t)
t^4
sage: weight([[4], [2]],t)
t^2