Hall-Littlewood Polynomials¶

class sage.combinat.sf.hall_littlewood.ElementHallLittlewood_generic_Element(M, x)¶

Bases: sage.combinat.sf.sfa.SymmetricFunctionAlgebra_generic_Element

expand(n, alphabet='x')¶

Expands the symmetric function as a symmetric polynomial in $n$ variables.

EXAMPLES:

sage: HLP  = HallLittlewoodP(QQ)
sage: HLQ  = HallLittlewoodQ(QQ)
sage: HLQp = HallLittlewoodQp(QQ)
sage: HLP([2]).expand(2)
x0^2 + (-t + 1)*x0*x1 + x1^2
sage: HLQ([2]).expand(2)
(-t + 1)*x0^2 + (t^2 - 2*t + 1)*x0*x1 + (-t + 1)*x1^2
sage: HLQp([2]).expand(2)
x0^2 + x0*x1 + x1^2

scalar(x)¶

Returns standard scalar product between self and s.

This is the default implementation that converts both self and x into Schur functions and performs the scalar product that basis.

EXAMPLES:

sage: HLP  = HallLittlewoodP(QQ)
sage: HLQ  = HallLittlewoodQ(QQ)
sage: HLQp = HallLittlewoodQp(QQ)
sage: HLP([2]).scalar(HLQp([2]))
1
sage: HLP([2]).scalar(HLQp([1,1]))
0

scalar_hl(x, t=None)¶

Returns the standard Hall-Littlewood scalar product of self and x.

EXAMPLES:

sage: HLP  = HallLittlewoodP(QQ)
sage: HLQ  = HallLittlewoodQ(QQ)
sage: HLQp = HallLittlewoodQp(QQ)
sage: HLP([2]).scalar_hl(HLQ([2]))
1
sage: HLP([2]).scalar_hl(HLQ([1,1]))
0

sage.combinat.sf.hall_littlewood.HallLittlewoodP(R, t=None)¶

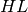Returns the algebra of symmetric functions in Hall-Littlewood $P$ basis. This is the same as the $HL$ basis in John Stembridge’s SF examples file.

If $t$ is not specified, then the base ring will be obtained by making the univariate polynomial ring over $R$ with the variable $t$ and taking its fraction field.

EXAMPLES:

sage: HallLittlewoodP(QQ)
Hall-Littlewood polynomials in the P basis over Fraction Field of Univariate Polynomial Ring in t over Rational Field
sage: HallLittlewoodP(QQ, t=-1)
Hall-Littlewood polynomials in the P basis with t=-1 over Rational Field
sage: HLP = HallLittlewoodP(QQ)
sage: s = SFASchur(HLP.base_ring())
sage: s(HLP([2,1]))
(-t^2-t)*s[1, 1, 1] + s[2, 1]

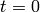The Hall-Littlewood polynomials in the $P$ basis at $t = 0$ are the Schur functions.

sage: HLP = HallLittlewoodP(QQ,t=0)
sage: s = SFASchur(HLP.base_ring())
sage: s(HLP([2,1])) == s([2,1])
True

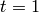The Hall-Littlewood polynomials in the $P$ basis at $t = 1$ are the monomial symmetric functions.

sage: HLP = HallLittlewoodP(QQ,t=1)
sage: m = SFAMonomial(HLP.base_ring())
sage: m(HLP([2,2,1])) == m([2,2,1])
True

We end with some examples of coercions between:

Hall-Littlewood $P$ basis.

Hall-Littlewood polynomials in the $Q$ basis

Hall-Littlewood polynomials in the $Q^\prime$ basis (via the Schurs)

Classical symmetric functions

EXAMPLES:

sage: HLP  = HallLittlewoodP(QQ)
sage: HLQ  = HallLittlewoodQ(QQ)
sage: HLQp = HallLittlewoodQp(QQ)
sage: s = SFASchur(HLP.base_ring()); p = SFAPower(HLP.base_ring()) 
sage: HLP(HLQ([2])) # indirect doctest
(-t+1)*P[2]
sage: HLP(HLQp([2]))
t*P[1, 1] + P[2]
sage: HLP(s([2]))
t*P[1, 1] + P[2]
sage: HLP(p([2]))
(t-1)*P[1, 1] + P[2]

sage.combinat.sf.hall_littlewood.HallLittlewoodQ(R, t=None)¶

Returns the algebra of symmetric functions in Hall-Littlewood 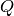$Q$ basis. This is the same as the 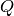$Q$ basis in John Stembridge’s SF examples file.

If $t$ is not specified, then the base ring will be obtained by making the univariate polynomial ring over $R$ with the variable $t$ and taking its fraction field.

EXAMPLES:

sage: HallLittlewoodQ(QQ)
Hall-Littlewood polynomials in the Q basis over Fraction Field of Univariate Polynomial Ring in t over Rational Field
sage: HallLittlewoodQ(QQ, t=-1)
Hall-Littlewood polynomials in the Q basis with t=-1 over Rational Field

sage.combinat.sf.hall_littlewood.HallLittlewoodQp(R, t=None)¶

Returns the algebra of symmetric functions in Hall-Littlewood 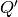$Q^\prime$ (Qp) basis. This is dual to the Hall-Littlewood $P$ basis with respect to the standard scalar product.

If $t$ is not specified, then the base ring will be obtained by making the univariate polynomial ring over $R$ with the variable $t$ and taking its fraction field.

EXAMPLES:

sage: HallLittlewoodQp(QQ)
Hall-Littlewood polynomials in the Qp basis over Fraction Field of Univariate Polynomial Ring in t over Rational Field
sage: HallLittlewoodQp(QQ, t=-1)
Hall-Littlewood polynomials in the Qp basis with t=-1 over Rational Field

class sage.combinat.sf.hall_littlewood.HallLittlewood_generic(R, t=None)¶

Bases: sage.combinat.sf.sfa.SymmetricFunctionAlgebra_generic

Element¶: alias of ElementHallLittlewood_generic_Element

transition_matrix(basis, n)¶

Returns the transitions matrix between self and basis for the homogenous component of degree n.

EXAMPLES:

sage: HLP = HallLittlewoodP(QQ)
sage: s   = SFASchur(HLP.base_ring())
sage: HLP.transition_matrix(s, 4)
[             1             -t              0            t^2           -t^3]
[             0              1             -t             -t      t^3 + t^2]
[             0              0              1             -t            t^3]
[             0              0              0              1 -t^3 - t^2 - t]
[             0              0              0              0              1]
sage: HLQ = HallLittlewoodQ(QQ)
sage: HLQ.transition_matrix(s,3)
[                        -t + 1                        t^2 - t                     -t^3 + t^2]
[                             0                  t^2 - 2*t + 1           -t^4 + t^3 + t^2 - t]
[                             0                              0 -t^6 + t^5 + t^4 - t^2 - t + 1]
sage: HLQp = HallLittlewoodQp(QQ)
sage: HLQp.transition_matrix(s,3)
[      1       0       0]
[      t       1       0]
[    t^3 t^2 + t       1]