Generic dual bases symmetric functions

class sage.combinat.sf.dual.SymmetricFunctionAlgebra_dual(dual_basis, scalar, scalar_name='', prefix=None)

Bases: sage.combinat.sf.classical.SymmetricFunctionAlgebra_classical

Element

alias of SymmetricFunctionAlgebra_dual_Element

dual_basis(scalar=None, scalar_name='', prefix=None)

Return the dual basis to self. If a the scalar option is not passed, then it returns the dual basis with respect to the scalar product used to define self.

EXAMPLES:

sage: m = SFAMonomial(QQ)
sage: zee = sage.combinat.sf.sfa.zee
sage: h = m.dual_basis(scalar=zee)
sage: h.dual_basis()
Symmetric Function Algebra over Rational Field, Monomial symmetric functions as basis
sage: m2 = h.dual_basis(zee, prefix='m2')
sage: m([2])^2
2*m[2, 2] + m[4]
sage: m2([2])^2
2*m2[2, 2] + m2[4]

transition_matrix(basis, n)

Returns the transition matrix between the 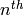homogeneous component of self and basis.

EXAMPLES:

sage: s = SFASchur(QQ)
sage: e = SFAElementary(QQ)
sage: f = e.dual_basis()
sage: f.transition_matrix(s, 5)
[ 1 -1  0  1  0 -1  1]
[-2  1  1 -1 -1  1  0]
[-2  2 -1 -1  1  0  0]
[ 3 -1 -1  1  0  0  0]
[ 3 -2  1  0  0  0  0]
[-4  1  0  0  0  0  0]
[ 1  0  0  0  0  0  0]
sage: e.transition_matrix(s, 5).inverse().transpose()
[ 1 -1  0  1  0 -1  1]
[-2  1  1 -1 -1  1  0]
[-2  2 -1 -1  1  0  0]
[ 3 -1 -1  1  0  0  0]
[ 3 -2  1  0  0  0  0]
[-4  1  0  0  0  0  0]
[ 1  0  0  0  0  0  0]

class sage.combinat.sf.dual.SymmetricFunctionAlgebra_dual_Element(A, dictionary=None, dual=None)

Bases: sage.combinat.sf.classical.SymmetricFunctionAlgebra_classical.Element

dual()

Returns self in the dual basis.

EXAMPLES:

sage: m = SFAMonomial(QQ)
sage: zee = sage.combinat.sf.sfa.zee
sage: h = m.dual_basis(scalar=zee)
sage: a = h([2,1])
sage: a.dual()
3*m[1, 1, 1] + 2*m[2, 1] + m[3]

expand(n, alphabet='x')

EXAMPLES:

sage: m = SFAMonomial(QQ)
sage: zee = sage.combinat.sf.sfa.zee
sage: h = m.dual_basis(zee)
sage: a = h([2,1])+h([3])
sage: a.expand(2)
2*x0^3 + 3*x0^2*x1 + 3*x0*x1^2 + 2*x1^3
sage: a.dual().expand(2)
2*x0^3 + 3*x0^2*x1 + 3*x0*x1^2 + 2*x1^3
sage: a.expand(2,alphabet='y')
2*y0^3 + 3*y0^2*y1 + 3*y0*y1^2 + 2*y1^3
sage: a.expand(2,alphabet='x,y')
2*x^3 + 3*x^2*y + 3*x*y^2 + 2*y^3

omega()

Returns the image of self under the Frobenius / omega automorphism.

EXAMPLES:

sage: m = SFAMonomial(QQ)
sage: zee = sage.combinat.sf.sfa.zee
sage: h = m.dual_basis(zee)
sage: hh = SFAHomogeneous(QQ)
sage: hh([2,1]).omega()
h[1, 1, 1] - h[2, 1]
sage: h([2,1]).omega()
d_m[1, 1, 1] - d_m[2, 1]

scalar(x)

Returns the standard scalar product of self and x.

EXAMPLES:

sage: m = SFAMonomial(QQ)
sage: zee = sage.combinat.sf.sfa.zee
sage: h = m.dual_basis(scalar=zee)
sage: a = h([2,1])
sage: a.scalar(a)
2

scalar_hl(x)

Returns the Hall-Littlewood scalar product of self and x.

EXAMPLES:

sage: m = SFAMonomial(QQ)
sage: zee = sage.combinat.sf.sfa.zee
sage: h = m.dual_basis(scalar=zee)
sage: a = h([2,1])
sage: a.scalar_hl(a)
(t + 2)/(-t^4 + 2*t^3 - 2*t + 1)