Power-sum symmetric functions

class sage.combinat.sf.powersum.SymmetricFunctionAlgebra_power(R)

Bases: sage.combinat.sf.multiplicative.SymmetricFunctionAlgebra_multiplicative

class Element(M, x)

Bases: sage.combinat.sf.classical.SymmetricFunctionAlgebra_classical.Element

expand(n, alphabet='x')

Expands the symmetric function as a symmetric polynomial in n variables.

EXAMPLES:

sage: p = SFAPower(QQ)
sage: a = p([2])
sage: a.expand(2)
x0^2 + x1^2
sage: a.expand(3, alphabet=['a','b','c'])
a^2 + b^2 + c^2
sage: p([2,1,1]).expand(2)
x0^4 + 2*x0^3*x1 + 2*x0^2*x1^2 + 2*x0*x1^3 + x1^4
sage: p([7]).expand(4)
x0^7 + x1^7 + x2^7 + x3^7
sage: p([7]).expand(4,alphabet='t')
t0^7 + t1^7 + t2^7 + t3^7
sage: p([7]).expand(4,alphabet='x,y,z,t')
x^7 + y^7 + z^7 + t^7

omega()

Returns the image of self under the Frobenius / omega automorphism.

EXAMPLES:

sage: p = SFAPower(QQ)
sage: a = p([2,1]); a
p[2, 1]
sage: a.omega()
-p[2, 1]

scalar(x)

Returns the standard scalar product of self and x.

Note that the power-sum symmetric functions are orthogonal under this scalar product. The value of 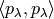is given by the size of the centralizer in 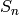of a permutation of cycle type .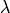

EXAMPLES:

sage: p = SFAPower(QQ)
sage: p4 = Partitions(4)
sage: matrix([ [p(a).scalar(p(b)) for a in p4] for b in p4])
[ 4  0  0  0  0]
[ 0  3  0  0  0]
[ 0  0  8  0  0]
[ 0  0  0  4  0]
[ 0  0  0  0 24]