Dynkin diagrams

sage.combinat.root_system.dynkin_diagram.DynkinDiagram(*args)

INPUT:

• ct - a Cartan Type

Returns a Dynkin diagram for type ct.

The edge multiplicities are encoded as edge labels. This uses the convention in Kac / Fulton Harris, Representation theory / Wikipedia (http://en.wikipedia.org/wiki/Dynkin_diagram). That is for i != j:

j --k--> i <==> a_ij = -k 
           <==> -scalar(coroot[i], root[j]) = k
           <==> multiple arrows point from the longer root 
                to the shorter one

EXAMPLES:

sage: DynkinDiagram(['A', 4])
O---O---O---O
1   2   3   4
A4

sage: DynkinDiagram(['A',1],['A',1])
O
1
O
2
A1xA1

sage: R = RootSystem("A2xB2xF4")
sage: DynkinDiagram(R)
O---O
1   2
O=>=O
3   4
O---O=>=O---O
5   6   7   8
A2xB2xF4

SEE ALSO: CartanType() for a general discussion on Cartan types and in particular node labeling conventions.

class sage.combinat.root_system.dynkin_diagram.DynkinDiagram_class(t=None)

Bases: sage.graphs.digraph.DiGraph, sage.combinat.root_system.cartan_type.CartanType_abstract

add_edge(i, j, label=1)

EXAMPLES:

sage: from sage.combinat.root_system.dynkin_diagram import DynkinDiagram_class
sage: d = DynkinDiagram_class(CartanType(['A',3]))
sage: list(sorted(d.edges()))
[]
sage: d.add_edge(2, 3)
sage: list(sorted(d.edges()))
[(2, 3, 1), (3, 2, 1)]

static an_instance()

Returns an example of Dynkin diagram

EXAMPLES:

sage: from sage.combinat.root_system.dynkin_diagram import DynkinDiagram_class
sage: g = DynkinDiagram_class.an_instance()
sage: g
Dynkin diagram of rank 3
sage: g.cartan_matrix()
[ 2 -1 -1]
[-2  2 -1]
[-1 -1  2]

cartan_matrix()

returns the Cartan matrix for this Dynkin diagram

EXAMPLES:

sage: DynkinDiagram(['C',3]).cartan_matrix()
[ 2 -1  0]
[-1  2 -2]
[ 0 -1  2]

cartan_type()

EXAMPLES:

sage: DynkinDiagram("A2","B2","F4").cartan_type()
A2xB2xF4

column(j)

Returns the 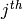column 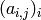of the Cartan matrix corresponding to this Dynkin diagram, as a container (or iterator) of tuples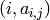

EXAMPLES:

sage: g = DynkinDiagram(["B",4])
sage: [ (i,a) for (i,a) in g.column(3) ]
[(3, 2), (2, -1), (4, -2)]

dual()

Returns the dual Dynkin diagram, obtained by reversing all edges.

EXAMPLES:

sage: D = DynkinDiagram(['C',3])
sage: D.edges()
[(1, 2, 1), (2, 1, 1), (2, 3, 1), (3, 2, 2)]
sage: D.dual()
O---O=>=O
1   2   3
B3
sage: D.dual().edges()
[(1, 2, 1), (2, 1, 1), (2, 3, 2), (3, 2, 1)]
sage: D.dual() == DynkinDiagram(['B',3])
True

TESTS:

sage: D = DynkinDiagram(['A',0]); D
A0
sage: D.edges()
[]
sage: D.dual()
A0
sage: D.dual().edges()
[]
sage: D = DynkinDiagram(['A',1])
sage: D.edges()
[]
sage: D.dual()
O
1
A1
sage: D.dual().edges()
[]

dynkin_diagram()

EXAMPLES:

sage: DynkinDiagram(['C',3]).dynkin_diagram()
O---O=<=O
1   2   3
C3

index_set()

EXAMPLES:

sage: DynkinDiagram(['C',3]).index_set()
[1, 2, 3]
sage: DynkinDiagram("A2","B2","F4").index_set()
[1, 2, 3, 4, 5, 6, 7, 8]

is_crystalographic()

Implements CartanType_abstract.is_crystalographic()

A Dynkin diagram always corresponds to a crystalographic root system.

rank()

Returns the index set for this Dynkin diagram

EXAMPLES:

sage: DynkinDiagram(['C',3]).rank()
3
sage: DynkinDiagram("A2","B2","F4").rank()
8

row(i)

Returns the 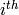row 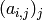of the Cartan matrix corresponding to this Dynkin diagram, as a container (or iterator) of tuples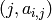

EXAMPLES:

sage: g = DynkinDiagram(["C",4])
sage: [ (i,a) for (i,a) in g.row(3) ]
[(3, 2), (2, -1), (4, -2)]

sage.combinat.root_system.dynkin_diagram.dynkin_diagram(t)

Returns the Dynkin diagram of type t.

Note that this function is deprecated, and that you should use DynkinDiagram instead as this will be disappearing in the near future.

EXAMPLES:

sage: dynkin_diagram(["A", 3])
doctest:1: DeprecationWarning: dynkin_diagram is deprecated, use DynkinDiagram instead!
O---O---O
1   2   3
A3

sage.combinat.root_system.dynkin_diagram.precheck(t, letter=None, length=None, affine=None, n_ge=None, n=None)

EXAMPLES:

sage: from sage.combinat.root_system.dynkin_diagram import precheck
sage: ct = CartanType(['A',4])
sage: precheck(ct, letter='C')
...
ValueError: t[0] must be = 'C'
sage: precheck(ct, affine=1)
...
ValueError: t[2] must be = 1
sage: precheck(ct, length=3)
...
ValueError: len(t) must be = 3
sage: precheck(ct, n=3)
...
ValueError: t[1] must be = 3
sage: precheck(ct, n_ge=5)
...
ValueError: t[1] must be >= 5