Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Root Systems »

Loosely speaking, Dynkin diagrams (or equivalently Cartan matrices) are graphs which are used to classify root systems, Coxeter and Weyl groups, Lie algebras, Lie groups, crystals, etc. up to an isomorphism. Cartan types are a standard set of names for those Dynkin diagrams.
http://en.wikipedia.org/wiki/Dynkin_diagram
Let us consider for example, the Cartan type 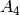 :
:
sage: T = CartanType(['A', 4])
sage: T
['A', 4]
It is the name of the following Dynkin diagram:
sage: DynkinDiagram(T)
O---O---O---O
1 2 3 4
A4
Note: for convenience, the following shortcuts are available:
sage: DynkinDiagram(['A',4])
O---O---O---O
1 2 3 4
A4
sage: DynkinDiagram('A4')
O---O---O---O
1 2 3 4
A4
sage: T.dynkin_diagram()
O---O---O---O
1 2 3 4
A4
See DynkinDiagram for how to further manipulate Dynkin diagrams.
From this data (the Cartan datum), one can construct the associated root system:
sage: RootSystem(T)
Root system of type ['A', 4]
The associated Weyl group is the symmetric group 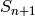 :
:
sage: W = WeylGroup(T)
sage: W
Weyl Group of type ['A', 4] (as a matrix group acting on the ambient space)
sage: W.cardinality()
120
while the Lie algebra is 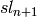 , and the Lie group
, and the Lie group 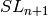 (TODO: illustrate this once this is implemented)
(TODO: illustrate this once this is implemented)
One may also construct crystals associated to various Dynkin diagrams. For example:
sage: C = CrystalOfLetters(T)
sage: C
The crystal of letters for type ['A', 4]
sage: C.list()
[1, 2, 3, 4, 5]
sage: C = CrystalOfTableaux(T, shape=[2])
sage: C
The crystal of tableaux of type ['A', 4] and shape(s) [[2]]
sage: C.cardinality()
15
Here is a sample of all the finite irreducible crystalographic Cartan types:
sage: CartanType.samples(finite = True, crystalographic = True)
[['A', 1], ['A', 5], ['B', 1], ['B', 5], ['C', 1], ['C', 5], ['D', 2], ['D', 3], ['D', 5],
['E', 6], ['E', 7], ['E', 8], ['F', 4], ['G', 2]]
Non-crystallographic Cartan types are also partially supported:
sage: CartanType.samples(finite = True, crystalographic = False)
[['I', 5], ['H', 3], ['H', 4]]
In Sage, a Cartan type is used as a database of type-specific information and algorithms (see e.g. sage.combinat.root_system.type_A). This database includes how to construct the Dynkin diagram, the ambient space for the root system (see http://en.wikipedia.org/wiki/Root_system), and further mathematical properties:
sage: T.is_finite(), T.is_simply_laced(), T.is_affine(), T.is_crystalographic()
(True, True, False, True)
It will eventually include Coxeter numbers, etc.
In particular, a Sage Cartan type is endowed with a fixed choice of labels for the nodes of the Dynkin diagram. This choice follows the conventions of Nicolas Bourbaki, Lie Groups and Lie Algebras: Chapter 4-6, Elements of Mathematics, Springer (2002). ISBN 978-3540426509. For example:
sage: T = CartanType(['D', 4])
sage: DynkinDiagram(T)
O 4
|
|
O---O---O
1 2 3
D4
sage: E6 = CartanType(['E',6])
sage: DynkinDiagram(E6)
O 2
|
|
O---O---O---O---O
1 3 4 5 6
E6
If desired, other node labelling conventions can be achieved. For example the Kac labelling for type ‘E_6` can be obtained via:
sage: E6.relabel({1:1,2:6,3:2,4:3,5:4,6:5}).dynkin_diagram()
O 6
|
|
O---O---O---O---O
1 2 3 4 5
E6 relabelled by {1: 1, 2: 6, 3: 2, 4: 3, 5: 4, 6: 5}
Contributions implementing other conventions are very welcome.
Another option is to build from scratch a new Dynkin diagram. The architecture has been designed to make it fairly easy to add other labelling conventions. In particular, we strived at choosing type free algorithms whenever possible, so in principle most feature should remain available even with custom Cartan types. This has not been used much yet, so some rough corners certainly remain.
Here, we construct the hyperbolic example of Exercise 4.9 p. 57 of Kac, Infinite Dimensional Lie Algebras. We start with an empty Dynkin diagram, and add a couple nodes:
sage: g = DynkinDiagram()
sage: g.add_vertices([1,2,3])
Note that the diagonal of the Cartan matrix is already initialized:
sage: g.cartan_matrix()
[2 0 0]
[0 2 0]
[0 0 2]
Then we add a couple edges:
sage: g.add_edge(1,2,2)
sage: g.add_edge(1,3)
sage: g.add_edge(2,3)
and we get the desired Cartan matrix:
sage: g.cartan_matrix()
[ 2 -1 -1]
[-2 2 -1]
[-1 -1 2]
Note that backward edges have been automatically added:
sage: g.edges()
[(1, 2, 2), (1, 3, 1), (2, 1, 1), (2, 3, 1), (3, 1, 1), (3, 2, 1)]
Caveat: the Dynkin diagram should not be modified after having been used; this is not checked currently (Todo: add a method set_mutable(), as for matrices).
Reducible Cartan types
Reducible Cartan types can be specified by passing a sequence or list of irreducible Cartan types:
sage: CartanType(['A',2],['B',2])
A2xB2
sage: CartanType([['A',2],['B',2]])
A2xB2
sage: CartanType(['A',2],['B',2]).is_reducible()
True
or using the following short hand notation:
sage: CartanType("A2xB2")
A2xB2
sage: CartanType("A2","B2") == CartanType("A2xB2")
True
Degenerate cases
When possible, type 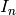 is automatically converted to the isomorphic
crystalographic Cartan types (any reason not to do so?):
is automatically converted to the isomorphic
crystalographic Cartan types (any reason not to do so?):
sage: CartanType(["I",1])
A1xA1
sage: CartanType(["I",3])
['A', 2]
sage: CartanType(["I",4])
['C', 2]
sage: CartanType(["I",6])
['G', 2]
The Dynkin diagrams for types 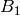 ,
, 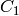 ,
, 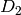 , and
, and 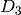 are
isomorphic to that for
are
isomorphic to that for 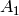 ,
, 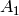 ,
, 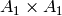 , and
, and 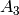 ,
respectively. However their natural ambient space realizations (stemming
from the corresponding infinite families of Lie groups) are different.
Therefore, the Cartan types are considered as distinct:
,
respectively. However their natural ambient space realizations (stemming
from the corresponding infinite families of Lie groups) are different.
Therefore, the Cartan types are considered as distinct:
sage: CartanType(['B',1])
['B', 1]
sage: CartanType(['C',1])
['C', 1]
sage: CartanType(['D',2])
['D', 2]
sage: CartanType(['D',3])
['D', 3]
Affine Cartan types
For affine types, we use the usual conventions for affine Coxeter groups: each affine type is either untwisted (that is arise from the natural affinisation of a finite cartan type):
sage: CartanType(["A", 4, 1]).dynkin_diagram()
0
O-----------+
| |
| |
O---O---O---O
1 2 3 4
A4~
sage: CartanType(["B", 4, 1]).dynkin_diagram()
O 0
|
|
O---O---O=>=O
1 2 3 4
B4~
or dual thereof:
sage: CartanType(["B", 4, 1]).dual().dynkin_diagram()
O 0
|
|
O---O---O=<=O
1 2 3 4
B4~*
or is of type 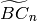 (which yields an irreducible, but nonreduced root system):
(which yields an irreducible, but nonreduced root system):
sage: CartanType(["BC", 4, 2]).dynkin_diagram()
O=<=O---O---O=<=O
0 1 2 3 4
BC4~
This includes the two degenerate cases:
sage: CartanType(["A", 1, 1]).dynkin_diagram()
O<=>O
0 1
A1~
sage: CartanType(["BC", 1, 2]).dynkin_diagram()
4
O=<=O
0 1
BC1~
For the user convenience, Kac’s notations for twisted affine types are automatically translated into the previous ones:
sage: CartanType(["A", 9, 2])
['B', 5, 1]^*
sage: CartanType(["A", 9, 2]).dynkin_diagram()
O 0
|
|
O---O---O---O=<=O
1 2 3 4 5
B5~*
sage: CartanType(["A", 10, 2]).dynkin_diagram()
O=<=O---O---O---O=<=O
0 1 2 3 4 5
BC5~
sage: CartanType(["D", 5, 2]).dynkin_diagram()
O=<=O---O---O=>=O
0 1 2 3 4
C4~*
sage: CartanType(["D", 4, 3]).dynkin_diagram()
3
O=>=O---O
2 1 0
G2~* relabelled by {0: 0, 1: 2, 2: 1}
sage: CartanType(["E", 6, 2]).dynkin_diagram()
O---O---O=<=O---O
0 1 2 3 4
F4~*
Bases: sage.structure.sage_object.SageObject
Returns a sample of the available Cartan types.
The sample contains all the exceptional finite and affine Cartan types, as well as typical representatives of the infinite families.
EXAMPLES:
sage: CartanType.samples()
[['A', 1], ['A', 5], ['B', 1], ['B', 5], ['C', 1], ['C', 5], ['D', 2], ['D', 3], ['D', 5],
['E', 6], ['E', 7], ['E', 8], ['F', 4], ['G', 2], ['I', 5], ['H', 3], ['H', 4],
['A', 1, 1], ['A', 5, 1], ['B', 1, 1], ['B', 5, 1],
['C', 1, 1], ['C', 5, 1], ['D', 3, 1], ['D', 5, 1],
['E', 6, 1], ['E', 7, 1], ['E', 8, 1], ['F', 4, 1], ['G', 2, 1],
['B', 5, 1]^*, ['C', 4, 1]^*, ['F', 4, 1]^*, ['G', 2, 1]^*,
['BC', 1, 2], ['BC', 5, 2]]
The finite, affine and crystalographic options allow respectively for restricting to (non) finite, (non) affine, and (non) crystalographic Cartan types:
sage: CartanType.samples(finite=True)
[['A', 1], ['A', 5], ['B', 1], ['B', 5], ['C', 1], ['C', 5], ['D', 2], ['D', 3], ['D', 5],
['E', 6], ['E', 7], ['E', 8], ['F', 4], ['G', 2], ['I', 5], ['H', 3], ['H', 4]]
sage: CartanType.samples(affine=True)
[['A', 1, 1], ['A', 5, 1], ['B', 1, 1], ['B', 5, 1],
['C', 1, 1], ['C', 5, 1], ['D', 3, 1], ['D', 5, 1],
['E', 6, 1], ['E', 7, 1], ['E', 8, 1], ['F', 4, 1], ['G', 2, 1],
['B', 5, 1]^*, ['C', 4, 1]^*, ['F', 4, 1]^*, ['G', 2, 1]^*,
['BC', 1, 2], ['BC', 5, 2]]
sage: CartanType.samples(crystalographic=True)
[['A', 1], ['A', 5], ['B', 1], ['B', 5], ['C', 1], ['C', 5], ['D', 2], ['D', 3], ['D', 5],
['E', 6], ['E', 7], ['E', 8], ['F', 4], ['G', 2],
['A', 1, 1], ['A', 5, 1], ['B', 1, 1], ['B', 5, 1],
['C', 1, 1], ['C', 5, 1], ['D', 3, 1], ['D', 5, 1],
['E', 6, 1], ['E', 7, 1], ['E', 8, 1], ['F', 4, 1], ['G', 2, 1],
['B', 5, 1]^*, ['C', 4, 1]^*, ['F', 4, 1]^*, ['G', 2, 1]^*,
['BC', 1, 2], ['BC', 5, 2]]
sage: CartanType.samples(crystalographic=False)
[['I', 5], ['H', 3], ['H', 4]]
Todo: add some reducible Cartan types (suggestions?)
Bases: object
Abstract class for Cartan types
Subclasses should implement:
- dynkin_diagram()
Returns the dual cartan type, possibly just as a formal dual.
EXAMPLES:
sage: CartanType(['A',3]).dual()
['A', 3]
sage: CartanType(["B", 3]).dual()
['C', 3]
sage: CartanType(['C',2]).dual()
['B', 2]
sage: CartanType(['D',4]).dual()
['D', 4]
sage: CartanType(['E',8]).dual()
['E', 8]
sage: CartanType(['F',4]).dual()
['F', 4]^*
Returns the index set for self. This is the list of the nodes of the associated Coxeter / Dynkin diagram.
EXAMPLES:
sage: CartanType(['A', 3, 1]).index_set()
[0, 1, 2, 3]
sage: CartanType(['D', 4]).index_set()
[1, 2, 3, 4]
sage: CartanType(['A', 7, 2]).index_set()
[0, 1, 2, 3, 4]
sage: CartanType(['A', 7, 2]).index_set()
[0, 1, 2, 3, 4]
sage: CartanType(['A', 6, 2]).index_set()
[0, 1, 2, 3]
sage: CartanType(['D', 6, 2]).index_set()
[0, 1, 2, 3, 4, 5]
sage: CartanType(['E', 6, 1]).index_set()
[0, 1, 2, 3, 4, 5, 6]
sage: CartanType(['E', 6, 2]).index_set()
[0, 1, 2, 3, 4]
sage: CartanType(['A', 2, 2]).index_set()
[0, 1]
sage: CartanType(['G', 2, 1]).index_set()
[0, 1, 2]
sage: CartanType(['F', 4, 1]).index_set()
[0, 1, 2, 3, 4]
Returns whether self is affine.
EXAMPLES:
sage: CartanType(['A', 3]).is_affine()
False
sage: CartanType(['A', 3, 1]).is_affine()
True
This method is usually equivalent to :meth:’.is_reducible’,
except for the Cartan type 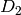 .
.
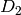 is not a standard Cartan type. It is equivalent to type
is not a standard Cartan type. It is equivalent to type
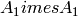 which is reducible; however the isomorphism
from its ambient space (for the orthogonal group of degree 4)
to that of
which is reducible; however the isomorphism
from its ambient space (for the orthogonal group of degree 4)
to that of 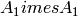 is non trivial, and it is useful to
have it.
is non trivial, and it is useful to
have it.
From a programming point of view its implementation is more similar to the irreducible types, and so the method is_atomic() is supplied.
EXAMPLES:
sage: CartanType("D2").is_atomic()
True
sage: CartanType("D2").is_irreducible()
False
TESTS:
sage: all( T.is_irreducible() == T.is_atomic() for T in CartanType.samples() if T != CartanType("D2"))
True
A short hand for not is_atomic().
TESTS:
sage: all( T.is_compound() == (not T.is_atomic()) for T in CartanType.samples())
True
Returns whether this Cartan type is crystalographic.
This returns False by default. Derived class should override this appropriately.
EXAMPLES:
sage: [ [t, t.is_crystalographic() ] for t in CartanType.samples(finite=True) ]
[[['A', 1], True], [['A', 5], True],
[['B', 1], True], [['B', 5], True],
[['C', 1], True], [['C', 5], True],
[['D', 2], True], [['D', 3], True], [['D', 5], True],
[['E', 6], True], [['E', 7], True], [['E', 8], True],
[['F', 4], True], [['G', 2], True],
[['I', 5], False], [['H', 3], False], [['H', 4], False]]
TESTS:
sage: all(t.is_crystalographic() for t in CartanType.samples(affine=True))
True
Returns whether this Cartan type is finite.
EXAMPLES:
sage: from sage.combinat.root_system.cartan_type import CartanType_abstract
sage: C = CartanType_abstract()
sage: C.is_finite()
...
NotImplementedError: <abstract method is_finite at ...>
sage: CartanType(['A',4]).is_finite()
True
sage: CartanType(['A',4, 1]).is_finite()
False
Report whether this Cartan type is irreducible (i.e. simple). This should be overridden in any subclass.
This returns False by default. Derived class should override this appropriately.
EXAMPLES:
sage: from sage.combinat.root_system.cartan_type import CartanType_abstract
sage: C = CartanType_abstract()
sage: C.is_irreducible()
False
Report whether the root system is reducible (i.e. not simple), that is whether it can be factored as a product of root systems.
EXAMPLES:
sage: CartanType("A2xB3").is_reducible()
True
sage: CartanType(['A',2]).is_reducible()
False
Returns whether this Cartan type is simply laced
This returns False by default. Derived class should override this appropriately.
EXAMPLES:
sage: [ [t, t.is_simply_laced() ] for t in CartanType.samples() ]
[[['A', 1], True], [['A', 5], True],
[['B', 1], True], [['B', 5], False],
[['C', 1], True], [['C', 5], False],
[['D', 2], True], [['D', 3], True], [['D', 5], True],
[['E', 6], True], [['E', 7], True], [['E', 8], True],
[['F', 4], False], [['G', 2], False], [['I', 5], False], [['H', 3], False], [['H', 4], False],
[['A', 1, 1], False], [['A', 5, 1], True],
[['B', 1, 1], False], [['B', 5, 1], False],
[['C', 1, 1], False], [['C', 5, 1], False],
[['D', 3, 1], True], [['D', 5, 1], True],
[['E', 6, 1], True], [['E', 7, 1], True], [['E', 8, 1], True],
[['F', 4, 1], False], [['G', 2, 1], False],
[['B', 5, 1]^*, False], [['C', 4, 1]^*, False], [['F', 4, 1]^*, False], [['G', 2, 1]^*, False],
[['BC', 1, 2], False], [['BC', 5, 2], False]]
Returns the rank of self, that is the number of nodes of the Dynkin diagram
EXAMPLES:
sage: CartanType(['A', 4]).rank()
4
sage: CartanType(['A', 7, 2]).rank()
5
sage: CartanType(['I', 8]).rank()
2
INPUT:
- type – a Cartan type
- relabelling – a function (or a list, or a dictionary)
Returns an isomorphic Cartan type obtained by relabelling the nodes of the dynkin diagram. Namely the node with label i is relabelled f(i) (or, by f[i] if f is a list or dictionary).
EXAMPLES:
sage: CartanType(['F',4]).relabel({ 1:4, 2:3, 3:2, 4:1 }).dynkin_diagram()
O---O=>=O---O
4 3 2 1
F4 relabelled by {1: 4, 2: 3, 3: 2, 4: 1}
Returns the root system associated to self.
EXAMPLES:
sage: CartanType(['A',4]).root_system()
Root system of type ['A', 4]
Returns the type of self, or None if unknown. This method should be overridden in any subclass.
EXAMPLES:
sage: from sage.combinat.root_system.cartan_type import CartanType_abstract
sage: C = CartanType_abstract()
sage: C.type() is None
True
Bases: sage.combinat.root_system.cartan_type.CartanType_simple, sage.combinat.root_system.cartan_type.CartanType_crystalographic
An abstract class for simple affine Cartan types
Return the unique minimal non trivial annihilating linear
combination of 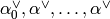 with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the columns of the
Cartan matrix with non-negative coefficients).
with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the columns of the
Cartan matrix with non-negative coefficients).
Throw an error if the existence or uniqueness does not hold
FIXME: the current implementation assumes that the Cartan
matrix is indexed by ![[0,1,...]](../../../_images/math/2163863982208b3c98d079780c71b0a38e3f4faa.png) , in the same order as the
index set.
, in the same order as the
index set.
EXAMPLES:
sage: RootSystem(['C',2,1]).cartan_type().a()
Finite family {0: 1, 1: 2, 2: 1}
sage: RootSystem(['D',4,1]).cartan_type().a()
Finite family {0: 1, 1: 1, 2: 2, 3: 1, 4: 1}
sage: RootSystem(['F',4,1]).cartan_type().a()
Finite family {0: 1, 1: 2, 2: 3, 3: 4, 4: 2}
sage: RootSystem(['BC',4,2]).cartan_type().a()
Finite family {0: 2, 1: 2, 2: 2, 3: 2, 4: 1}
Return the unique minimal non trivial annihilating linear
combination of 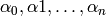 with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the rows of the
Cartan matrix with non-negative coefficients).
with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the rows of the
Cartan matrix with non-negative coefficients).
Throw an error if the existence of uniqueness does not hold
The optional argument m is for internal use only.
EXAMPLES:
sage: RootSystem(['C',2,1]).cartan_type().acheck()
Finite family {0: 1, 1: 1, 2: 1}
sage: RootSystem(['D',4,1]).cartan_type().acheck()
Finite family {0: 1, 1: 1, 2: 2, 3: 1, 4: 1}
sage: RootSystem(['F',4,1]).cartan_type().acheck()
Finite family {0: 1, 1: 2, 2: 3, 3: 2, 4: 1}
sage: RootSystem(['BC',4,2]).cartan_type().acheck()
Finite family {0: 1, 1: 2, 2: 2, 3: 2, 4: 2}
![[0,1,...]](../../../_images/math/2163863982208b3c98d079780c71b0a38e3f4faa.png) , in the same order as the index set.
, in the same order as the index set.Returns the family (c_i)_i of integer coefficients defined by
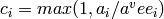 (see e.g. [FSS07] p. 3)
(see e.g. [FSS07] p. 3)
FIXME: the current implementation assumes that the Cartan
matrix is indexed by ![[0,1,...]](../../../_images/math/2163863982208b3c98d079780c71b0a38e3f4faa.png) , in the same order as the
index set.
, in the same order as the
index set.
EXAMPLES:
sage: RootSystem(['C',2,1]).cartan_type().c()
Finite family {0: 1, 1: 2, 2: 1}
sage: RootSystem(['D',4,1]).cartan_type().c()
Finite family {0: 1, 1: 1, 2: 1, 3: 1, 4: 1}
sage: RootSystem(['F',4,1]).cartan_type().c()
Finite family {0: 1, 1: 1, 2: 1, 3: 2, 4: 2}
sage: RootSystem(['BC',4,2]).cartan_type().c()
Finite family {0: 2, 1: 1, 2: 1, 3: 1, 4: 1}
TESTS:
sage: CartanType(["B", 3, 1]).c().map(parent)
Finite family {0: Integer Ring, 1: Integer Ring, 2: Integer Ring, 3: Integer Ring}
REFERENCES:
| [FSS07] | G. Fourier, A. Schilling, and M. Shimozono, Demazure structure inside Kirillov-Reshetikhin crystals, J. Algebra, Vol. 309, (2007), p. 386-404 http://arxiv.org/abs/math/0605451 |
Returns the classical Cartan type associated with this affine Cartan type.
EXAMPLES:
sage: CartanType(['A', 1, 1]).classical()
['A', 1]
sage: CartanType(['A', 3, 1]).classical()
['A', 3]
sage: CartanType(['B', 3, 1]).classical()
['B', 3]
sage: CartanType(['A', 2, 2]).classical()
['C', 1]
sage: CartanType(['BC', 1, 2]).classical()
['C', 1]
sage: CartanType(['A', 4, 2]).classical()
['C', 2]
sage: CartanType(['BC', 2, 2]).classical()
['C', 2]
sage: CartanType(['A', 10, 2]).classical()
['C', 5]
sage: CartanType(['BC', 5, 2]).classical()
['C', 5]
sage: CartanType(['D', 5, 2]).classical()
['B', 4]
sage: CartanType(['E', 6, 1]).classical()
['E', 6]
sage: CartanType(['G', 2, 1]).classical()
['G', 2]
sage: CartanType(['E', 6, 2]).classical() # todo: double check
['F', 4]^*
sage: CartanType(['D', 4, 3]).classical() # todo: double check
['G', 2]^* relabelled by {1: 2, 2: 1}
We check that classical(), dynkin_diagram(), and special_node() are consistent:
sage: for ct in CartanType.samples(affine = True):
... g1 = ct.classical().dynkin_diagram()
... g2 = ct.dynkin_diagram()
... g2.delete_vertex(ct.special_node())
... assert sorted(g1.vertices()) == sorted(g2.vertices())
... assert sorted(g1.edges()) == sorted(g2.edges())
Return the unique minimal non trivial annihilating linear
combination of 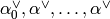 with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the columns of the
Cartan matrix with non-negative coefficients).
with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the columns of the
Cartan matrix with non-negative coefficients).
Throw an error if the existence or uniqueness does not hold
FIXME: the current implementation assumes that the Cartan
matrix is indexed by ![[0,1,...]](../../../_images/math/2163863982208b3c98d079780c71b0a38e3f4faa.png) , in the same order as the
index set.
, in the same order as the
index set.
EXAMPLES:
sage: RootSystem(['C',2,1]).cartan_type().a()
Finite family {0: 1, 1: 2, 2: 1}
sage: RootSystem(['D',4,1]).cartan_type().a()
Finite family {0: 1, 1: 1, 2: 2, 3: 1, 4: 1}
sage: RootSystem(['F',4,1]).cartan_type().a()
Finite family {0: 1, 1: 2, 2: 3, 3: 4, 4: 2}
sage: RootSystem(['BC',4,2]).cartan_type().a()
Finite family {0: 2, 1: 2, 2: 2, 3: 2, 4: 1}
EXAMPLES:
sage: CartanType(['A', 3, 1]).is_affine()
True
EXAMPLES:
sage: CartanType(['A', 3, 1]).is_finite()
False
Returns whether self is untwisted affine, that is if it is the affine extension of some finite type.
Every affine type is either untwisted affine, or dual thereof or of type BC.
EXAMPLES:
sage: CartanType(['A', 3, 1]).is_untwisted_affine()
True
sage: CartanType(['A', 3, 1]).dual().is_untwisted_affine() # this one is self dual!
True
sage: CartanType(['B', 3, 1]).dual().is_untwisted_affine()
False
sage: CartanType(['BC', 3, 2]).is_untwisted_affine()
False
Return the unique minimal non trivial annihilating linear
combination of 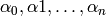 with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the rows of the
Cartan matrix with non-negative coefficients).
with
nonnegative coefficients (or alternatively, the unique minimal
non trivial annihilating linear combination of the rows of the
Cartan matrix with non-negative coefficients).
Throw an error if the existence of uniqueness does not hold
The optional argument m is for internal use only.
EXAMPLES:
sage: RootSystem(['C',2,1]).cartan_type().acheck()
Finite family {0: 1, 1: 1, 2: 1}
sage: RootSystem(['D',4,1]).cartan_type().acheck()
Finite family {0: 1, 1: 1, 2: 2, 3: 1, 4: 1}
sage: RootSystem(['F',4,1]).cartan_type().acheck()
Finite family {0: 1, 1: 2, 2: 3, 3: 2, 4: 1}
sage: RootSystem(['BC',4,2]).cartan_type().acheck()
Finite family {0: 1, 1: 2, 2: 2, 3: 2, 4: 2}
![[0,1,...]](../../../_images/math/2163863982208b3c98d079780c71b0a38e3f4faa.png) , in the same order as the index set.
, in the same order as the index set.A special node is a node of the Dynkin diagram such that pruning it yields a Dynkin diagram for the associated classical type (see classical()).
This method returns the label of some special node. This is
usually  in the standard conventions.
in the standard conventions.
EXAMPLES:
sage: CartanType(['A', 3, 1]).special_node()
0
The choice is guaranteed to be consistent with the indexing of the nodes of the classical Dynkin diagram:
sage: CartanType(['A', 3, 1]).index_set()
[0, 1, 2, 3]
sage: CartanType(['A', 3, 1]).classical().index_set()
[1, 2, 3]
Returns the translation factors for self. Those are the
smallest factors 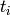 such that the translation by
such that the translation by 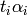 maps the fundamental polygon to another polygon in
the alcove picture.
maps the fundamental polygon to another polygon in
the alcove picture.
OUTPUT: a dictionary from self.index_set() to  (or
(or  for affine type
for affine type 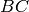 )
)
Those coefficients are all  for dual untwisted, and in
particular for simply laced. They coincide with the usual
for dual untwisted, and in
particular for simply laced. They coincide with the usual
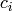 coefficients (see c()) for untwisted and dual
thereof. See the discussion below for affine type
coefficients (see c()) for untwisted and dual
thereof. See the discussion below for affine type 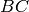 .
.
Note: one usually realizes the alcove picture in the coweight lattice, with translations by coroots; in that case, one will use the translation factors for the dual Cartan type.
FIXME: the current implementation assumes that the Cartan
matrix is indexed by ![[0,1,...]](../../../_images/math/2163863982208b3c98d079780c71b0a38e3f4faa.png) , in the same order as the
index set.
, in the same order as the
index set.
EXAMPLES:
sage: CartanType(['C',2,1]).translation_factors()
Finite family {0: 1, 1: 2, 2: 1}
sage: CartanType(['C',2,1]).dual().translation_factors()
Finite family {0: 1, 1: 1, 2: 1}
sage: CartanType(['D',4,1]).translation_factors()
Finite family {0: 1, 1: 1, 2: 1, 3: 1, 4: 1}
sage: CartanType(['F',4,1]).translation_factors()
Finite family {0: 1, 1: 1, 2: 1, 3: 2, 4: 2}
sage: CartanType(['BC',4,2]).translation_factors()
Finite family {0: 1, 1: 1, 2: 1, 3: 1, 4: 1/2}
We proceed with systematic tests taken from MuPAD-Combinat’s testsuite:
sage: list(CartanType(["A", 1, 1]).translation_factors())
[1, 1]
sage: list(CartanType(["A", 5, 1]).translation_factors())
[1, 1, 1, 1, 1, 1]
sage: list(CartanType(["B", 5, 1]).translation_factors())
[1, 1, 1, 1, 1, 2]
sage: list(CartanType(["C", 5, 1]).translation_factors())
[1, 2, 2, 2, 2, 1]
sage: list(CartanType(["D", 5, 1]).translation_factors())
[1, 1, 1, 1, 1, 1]
sage: list(CartanType(["E", 6, 1]).translation_factors())
[1, 1, 1, 1, 1, 1, 1]
sage: list(CartanType(["E", 7, 1]).translation_factors())
[1, 1, 1, 1, 1, 1, 1, 1]
sage: list(CartanType(["E", 8, 1]).translation_factors())
[1, 1, 1, 1, 1, 1, 1, 1, 1]
sage: list(CartanType(["F", 4, 1]).translation_factors())
[1, 1, 1, 2, 2]
sage: list(CartanType(["G", 2, 1]).translation_factors())
[1, 3, 1]
sage: list(CartanType(["A", 2, 2]).translation_factors())
[1, 1/2]
sage: list(CartanType(["A", 2, 2]).dual().translation_factors())
[1/2, 1]
sage: list(CartanType(["A", 10, 2]).translation_factors())
[1, 1, 1, 1, 1, 1/2]
sage: list(CartanType(["A", 10, 2]).dual().translation_factors())
[1/2, 1, 1, 1, 1, 1]
sage: list(CartanType(["A", 9, 2]).translation_factors())
[1, 1, 1, 1, 1, 1]
sage: list(CartanType(["D", 5, 2]).translation_factors())
[1, 1, 1, 1, 1]
sage: list(CartanType(["D", 4, 3]).translation_factors())
[1, 1, 1]
sage: list(CartanType(["E", 6, 2]).translation_factors())
[1, 1, 1, 1, 1]
We conclude with a discussion of the appropriate value for
affine type 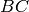 . Let us consider the alcove picture realized
in the weight lattice. It is obtained by taking the level-
. Let us consider the alcove picture realized
in the weight lattice. It is obtained by taking the level- affine hyperplane in the weight lattice, and projecting it
along
affine hyperplane in the weight lattice, and projecting it
along 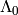 :
:
sage: R = RootSystem(["BC",2,2])
sage: alpha = R.weight_space().simple_roots()
sage: alphacheck = R.coroot_space().simple_roots()
sage: Lambda = R.weight_space().fundamental_weights()
Here are the levels of the fundamental weights:
sage: Lambda[0].level(), Lambda[1].level(), Lambda[2].level()
(1, 2, 2)
So the “center” of the fundamental polygon at level  is:
is:
sage: O = Lambda[0]
sage: O.level()
1
We take the projection 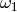 at level
at level  of
of 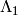 as unit vector on the
as unit vector on the  -axis, and the projection
-axis, and the projection 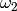 at level 0 of
at level 0 of 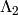 as unit vector of the
as unit vector of the  -axis:
-axis:
sage: omega1 = Lambda[1]-2*Lambda[0]
sage: omega2 = Lambda[2]-2*Lambda[0]
sage: omega1.level(), omega2.level()
(0, 0)
The projections of the simple roots can be read off:
sage: alpha[0]
2*Lambda[0] - Lambda[1]
sage: alpha[1]
-2*Lambda[0] + 2*Lambda[1] - Lambda[2]
sage: alpha[2]
-2*Lambda[1] + 2*Lambda[2]
Namely 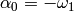 ,
, 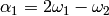 and
and 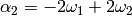 .
.
The reflection hyperplane defined by 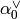 goes
through the points
goes
through the points 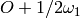 and
and 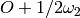 :
:
sage: (O+(1/2)*omega1).scalar(alphacheck[0])
0
sage: (O+(1/2)*omega2).scalar(alphacheck[0])
0
Hence, the fundamental alcove is the triangle 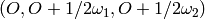 . By successive reflections, one can
tile the full plane. This induces a tiling of the full plane
by translates of the fundamental polygon.
. By successive reflections, one can
tile the full plane. This induces a tiling of the full plane
by translates of the fundamental polygon.
TODO: add the picture here, once root system plots in the weight lattice will be implemented. In the mean time, the reader may look up the dual picture on Figure 2 of [HST09] which was produced by MuPAD-Combinat.
From this picture, one can read that translations by
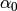 ,
, 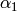 , and
, and 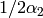 map the fundamental
polygon to translates of it in the alcove picture, and are
smallest with this property. Hence, the translation factors
for affine type
map the fundamental
polygon to translates of it in the alcove picture, and are
smallest with this property. Hence, the translation factors
for affine type 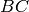 are
are 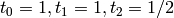 :
:
sage: CartanType(['BC',2,2]).translation_factors()
Finite family {0: 1, 1: 1, 2: 1/2}
TESTS:
sage: CartanType(["B", 3, 1]).translation_factors().map(parent)
Finite family {0: Integer Ring, 1: Integer Ring, 2: Integer Ring, 3: Integer Ring}
sage: CartanType(["BC", 3, 2]).translation_factors().map(parent)
Finite family {0: Integer Ring, 1: Integer Ring, 2: Integer Ring, 3: Rational Field}
REFERENCES:
| [HST09] | F. Hivert, A. Schilling, and N. M. Thiery, Hecke group algebras as quotients of affine Hecke algebras at level 0, JCT A, Vol. 116, (2009) p. 844-863 http://arxiv.org/abs/0804.3781 |
Bases: sage.combinat.root_system.cartan_type.CartanType_abstract
An abstract class for crystalographic cartan types
Returns the Cartan matrix associated with self.
EXAMPLES:
sage: CartanType(['A',4]).cartan_matrix()
[ 2 -1 0 0]
[-1 2 -1 0]
[ 0 -1 2 -1]
[ 0 0 -1 2]
Returns the Dynkin diagram associated with self.
EXAMPLES:
sage: CartanType(['A',4]).dynkin_diagram()
O---O---O---O
1 2 3 4
A4
Note: derived subclasses should typically implement this as a cached method
Implements CartanType_abstract.is_crystalographic()
by returning 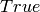 .
.
EXAMPLES:
sage: CartanType(['A', 3, 1]).is_crystalographic()
True
A Cartan matrix  is symmetrizable if there exists a non
trivial diagonal matrix
is symmetrizable if there exists a non
trivial diagonal matrix  such that
such that 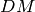 is a symmetric
matrix, that is
is a symmetric
matrix, that is 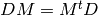 . In that case,
. In that case,  is unique, up
to a scalar factor for each connected component of the Dynkin
diagram.
is unique, up
to a scalar factor for each connected component of the Dynkin
diagram.
This method currently assumes that the Cartan type is irreducible.
This method computes the unique minimal such  with non
negative integral coefficients. If
with non
negative integral coefficients. If  exists, it is returned
as a family. Otherwise None is returned.
exists, it is returned
as a family. Otherwise None is returned.
EXAMPLES:
sage: CartanType(["B",5]).symmetrizer()
Finite family {1: 2, 2: 2, 3: 2, 4: 2, 5: 1}
Here is a neat trick to visualize it better:
sage: T = CartanType(["B",5])
sage: print T.ascii_art(T.symmetrizer().__getitem__)
O---O---O---O=>=O
2 2 2 2 1
sage: T = CartanType(["BC",5, 2])
sage: print T.ascii_art(T.symmetrizer().__getitem__)
O=<=O---O---O---O=<=O
1 2 2 2 2 4
Property: up to an overall scalar factor, this gives the norm of the simple roots in the ambient space:
sage: T = CartanType(["C",5])
sage: print T.ascii_art(T.symmetrizer().__getitem__)
O---O---O---O=<=O
1 1 1 1 2
sage: alpha = RootSystem(T).ambient_space().simple_roots()
sage: print T.ascii_art(lambda i: alpha[i].scalar(alpha[i]))
O---O---O---O=<=O
2 2 2 2 4
Bases: sage.combinat.root_system.cartan_type.CartanType_abstract
An abstract class for simple affine Cartan types
EXAMPLES:
sage: CartanType(["A", 3]).is_affine()
False
EXAMPLES:
sage: CartanType(["A", 3]).is_finite()
True
Bases: sage.combinat.root_system.cartan_type.CartanType_abstract
An abstract class for simple Cartan types
EXAMPLES:
sage: CartanType(['A', 3]).is_irreducible()
True
Bases: sage.combinat.root_system.cartan_type.CartanType_crystalographic
An abstract class for simply laced cartan types
Simply laced cartan types are self dual
EXAMPLES:
sage: CartanType(["A", 3]).dual()
['A', 3]
sage: CartanType(["A", 3, 1]).dual()
['A', 3, 1]
sage: CartanType(["D", 3]).dual()
['D', 3]
sage: CartanType(["D", 4, 1]).dual()
['D', 4, 1]
sage: CartanType(["E", 6]).dual()
['E', 6]
sage: CartanType(["E", 6, 1]).dual()
['E', 6, 1]
EXAMPLES:
sage: CartanType(['A',3,1]).is_simply_laced()
True
sage: CartanType(['A',2]).is_simply_laced()
True
Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.sage_object.SageObject, sage.combinat.root_system.cartan_type.CartanType_affine
A concrete class for affine simple Cartan types
Implements CartanType_abstract.index_set().
The index set for all standard affine Cartan types is of the form 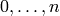 .
.
EXAMPLES:
sage: CartanType(['A', 4, 1]).rank()
5
sage: CartanType(['B', 4, 1]).rank()
5
sage: CartanType(['C', 3, 1]).rank()
4
sage: CartanType(['D', 4, 1]).rank()
5
sage: CartanType(['E', 6, 1]).rank()
7
sage: CartanType(['E', 7, 1]).rank()
8
sage: CartanType(['F', 4, 1]).rank()
5
sage: CartanType(['G', 2, 1]).rank()
3
sage: CartanType(['A', 2, 2]).rank()
2
sage: CartanType(['A', 6, 2]).rank()
4
sage: CartanType(['A', 7, 2]).rank()
5
sage: CartanType(['D', 5, 2]).rank()
5
sage: CartanType(['E', 6, 2]).rank()
5
sage: CartanType(['D', 4, 3]).rank()
3
Implements :meth:’CartanType_abstract.special_node`.
With the standard labelling conventions,  is always a
special node.
is always a
special node.
EXAMPLES:
sage: CartanType(['A', 3, 1]).special_node()
0
Returns the type of self.
EXAMPLES:
sage: CartanType(['A', 4, 1]).type()
'A'
Bases: sage.structure.unique_representation.UniqueRepresentation, sage.structure.sage_object.SageObject, sage.combinat.root_system.cartan_type.CartanType_finite
A concrete base class for the finite standard Cartan types 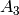 ,
, 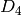 ,
, 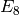
Returns the corresponding untwisted affine Cartan type
EXAMPLES:
sage: CartanType(['A',3]).affine()
['A', 3, 1]
Implements CartanType_abstract.index_set().
The index set for all standard finite Cartan types is of the form 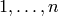 .
(but see type_I for a slight abuse of this).
.
(but see type_I for a slight abuse of this).
EXAMPLES:
sage: CartanType(['A', 3]).rank()
3
sage: CartanType(['B', 3]).rank()
3
sage: CartanType(['C', 3]).rank()
3
sage: CartanType(['D', 4]).rank()
4
sage: CartanType(['E', 6]).rank()
6
Returns the type of self.
EXAMPLES:
sage: CartanType(['A', 4]).type()
'A'
sage: CartanType(['A', 4, 1]).type()
'A'
Bases: sage.combinat.root_system.cartan_type.CartanType_standard_affine
A concrete class for the standard untwisted affine Cartan types
Returns the classical Cartan type associated with self (which should be affine)
EXAMPLES:
sage: CartanType(['A', 3, 1]).classical()
['A', 3]
sage: CartanType(['B', 3, 1]).classical()
['B', 3]
sage: CartanType(['C', 3, 1]).classical()
['C', 3]
sage: CartanType(['D', 4, 1]).classical()
['D', 4]
sage: CartanType(['E', 6, 1]).classical()
['E', 6]
sage: CartanType(['F', 4, 1]).classical()
['F', 4]
sage: CartanType(['G', 2, 1]).classical()
['G', 2]
Implements :meth:’CartanType_affine.is_untwisted_affine` by returning True.
EXAMPLES:
sage: CartanType(['B', 3, 1]).is_untwisted_affine()
True