Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Posets »

Bases: sage.structure.parent_base.ParentWithBase
Note
A class that inherits from this class needs to define _element_type. This is the class of the elements that the inheriting class contains. For example, for this class, FinitePoset, _element_type is PosetElement.
Returns a list of all antichains of the poset.
An antichain of a poset is a collection of elements of the poset that are pairwise incomparable.
EXAMPLES:
sage: Posets.PentagonPoset().antichains()
[[], [0], [1], [2], [3], [4], [1, 2], [1, 3]]
sage: Posets.AntichainPoset(3).antichains()
[[], [2], [1], [0], [1, 0], [2, 1], [2, 0], [2, 1, 0]]
sage: Posets.ChainPoset(3).antichains()
[[], [0], [1], [2]]
Returns the bottom element of the poset, if it exists.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P.bottom() is None
True
sage: Q = Poset({0:[1],1:[]})
sage: Q.bottom()
0
Returns the number of elements in the poset.
EXAMPLES:
sage: Poset([[1,2,3],[4],[4],[4],[]]).cardinality()
5
Returns a list of the elements  such that
such that 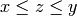 .
The order is that induced by the ordering in
self.linear_extension().
.
The order is that induced by the ordering in
self.linear_extension().
EXAMPLES:
sage: uc = [[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]]
sage: dag = DiGraph(dict(zip(range(len(uc)),uc)))
sage: P = Poset(dag)
sage: I = set(map(P,[2,5,6,4,7]))
sage: I == set(P.closed_interval(2,7))
True
Compare x and y in the poset.
If x = y, then 0 is returned; if x < y, then -1 is returned; if x > y, then 1 is returned; and if x and y are not comparable, then None is returned.
EXAMPLES:
sage: P = Poset([[1,2],[4],[3],[4],[]])
sage: P(0)._cmp(P(0))
0
sage: P(0)._cmp(P(4))
-1
sage: P(4)._cmp(P(0))
1
sage: P(1)._cmp(P(2))
Returns the list of pairs [u,v] of elements of the poset such that u v is a cover relation (that is, u v and there does not exist z such that u z v).
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: Q.cover_relations()
[[1, 2], [0, 2], [2, 3], [3, 4]]
Returns an iterator for the cover relations of the poset.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: type(Q.cover_relations_iterator())
<type 'generator'>
sage: [z for z in Q.cover_relations_iterator()]
[[1, 2], [0, 2], [2, 3], [3, 4]]
Returns True if y covers x and False otherwise.
EXAMPLES:
sage: Q = Poset([[1,5],[2,6],[3],[4],[],[6,3],[4]])
sage: Q.covers(Q(1),Q(6))
True
sage: Q.covers(Q(1),Q(4))
False
Create an aliased version of a function or a method which raise a deprecation warning message.
If f is a function or a method, write g = deprecated_function_alias(f, "Sage version") to make a deprecated aliased version of f.
INPUT:
- func - the function or method to be aliased
- version - the version of sage when the function is deprecated
EXAMPLES:
sage: from sage.misc.misc import deprecated_function_alias
sage: g = deprecated_function_alias(number_of_partitions,
... 'Sage Version 42.132')
sage: g(5)
doctest:...: DeprecationWarning: (Since Sage Version 42.132) g is deprecated. Please use number_of_partitions instead.
7
This also works for methods:
sage: class cls(object):
... def new_meth(self): return 42
... old_meth = deprecated_function_alias(new_meth,
... 'Sage Version 42.132')
sage: cls().old_meth()
doctest:...: DeprecationWarning: (Since Sage Version 42.132) old_meth is deprecated. Please use new_meth instead.
42
AUTHORS:
- Florent Hivert (2009-11-23), with the help of Mike Hansen.
Returns the dual poset of the given poset.
EXAMPLE:
sage: P = Poset([[1,2],[4],[3],[4],[]])
sage: P.dual()
Finite poset containing 5 elements
Returns a representation in the DOT language, ready to render in graphviz.
REFERENCES:
EXAMPLES:
sage: P = Poset({'a':['b'],'b':['d'],'c':['d'],'d':['f'],'e':['f'],'f':[]})
sage: print P.graphviz_string()
graph {
"f";"d";"b";"a";"c";"e";
"f"--"e";"d"--"c";"b"--"a";"d"--"b";"f"--"d";
}
Returns True if the poset has a unique minimal element.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P.has_bottom()
False
sage: Q = Poset({0:[1],1:[]})
sage: Q.has_bottom()
True
Returns True if the poset contains a unique maximal element, and False otherwise.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4,5],4:[],5:[]})
sage: P.has_top()
False
sage: Q = Poset({0:[1],1:[]})
sage: Q.has_top()
True
Returns the Hasse_diagram of the poset as a Sage DiGraph object.
EXAMPLES:
sage: Q = Poset({5:[2,3], 1:[3,4], 2:[0], 3:[0], 4:[0]})
sage: Q.hasse_diagram()
Hasse diagram of a poset containing 6 elements
sage: P = Poset({'a':['b'],'b':['d'],'c':['d'],'d':['f'],'e':['f'],'f':[]})
sage: H = P.hasse_diagram()
sage: P.cover_relations()
[[e, f], [c, d], [a, b], [b, d], [d, f]]
sage: H.edges()
[(a, b, None), (c, d, None), (b, d, None), (e, f, None), (d, f, None)]
Returns a list of the elements  such that
such that 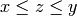 .
The order is that induced by the ordering in
self.linear_extension().
.
The order is that induced by the ordering in
self.linear_extension().
INPUT:
EXAMPLES:
sage: uc = [[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]]
sage: dag = DiGraph(dict(zip(range(len(uc)),uc)))
sage: P = Poset(dag)
sage: I = set(map(P,[2,5,6,4,7]))
sage: I == set(P.interval(2,7))
True
sage: dg = DiGraph({"a":["b","c"], "b":["d"], "c":["d"]})
sage: P = Poset(dg)
sage: P.interval("a","d")
[a, c, b, d]
Returns True if the poset contains a unique maximal element and a unique minimal element, and False otherwise.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4,5],4:[],5:[]})
sage: P.is_bounded()
False
sage: Q = Poset({0:[1],1:[]})
sage: Q.is_bounded()
True
Returns True if the poset is totally ordered, and False otherwise.
EXAMPLES:
sage: L = Poset({0:[1],1:[2],2:[3],3:[4]})
sage: L.is_chain()
True
sage: V = Poset({0:[1,2]})
sage: V.is_chain()
False
Returns True if x is greater than or equal to y in the poset, and False otherwise.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = Q(0),Q(1),Q(4)
sage: Q.is_gequal(x,y)
False
sage: Q.is_gequal(y,x)
False
sage: Q.is_gequal(x,z)
False
sage: Q.is_gequal(z,x)
True
sage: Q.is_gequal(z,y)
True
sage: Q.is_gequal(z,z)
True
Returns True if the poset is graded, and False otherwise.
A poset is graded if it admits a rank function.
EXAMPLES:
sage: P = Poset([[1],[2],[3],[4],[]])
sage: P.is_graded()
True
sage: Q = Poset([[1,5],[2,6],[3],[4],[],[6,3],[4]])
sage: Q.is_graded()
False
Returns True if x is greater than but not equal to y in the poset, and False otherwise.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = Q(0),Q(1),Q(4)
sage: Q.is_greater_than(x,y)
False
sage: Q.is_greater_than(y,x)
False
sage: Q.is_greater_than(x,z)
False
sage: Q.is_greater_than(z,x)
True
sage: Q.is_greater_than(z,y)
True
sage: Q.is_greater_than(z,z)
False
Returns True is the poset has a join operation, and False otherwise.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: P.is_join_semilattice()
True
sage: P = Poset([[1,2],[3],[3],[]])
sage: P.is_join_semilattice()
True
sage: P = Poset({0:[2,3],1:[2,3]})
sage: P.is_join_semilattice()
False
Returns True if x is less than or equal to y in the poset, and False otherwise.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = Q(0),Q(1),Q(4)
sage: Q.is_lequal(x,y)
False
sage: Q.is_lequal(y,x)
False
sage: Q.is_lequal(x,z)
True
sage: Q.is_lequal(y,z)
True
sage: Q.is_lequal(z,z)
True
Returns True if x is less than but not equal to y in the poset, and False otherwise.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = Q(0),Q(1),Q(4)
sage: Q.is_less_than(x,y)
False
sage: Q.is_less_than(y,x)
False
sage: Q.is_less_than(x,z)
True
sage: Q.is_less_than(y,z)
True
sage: Q.is_less_than(z,z)
False
Returns True if self has a meet operation, and False otherwise.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: P.is_meet_semilattice()
True
sage: P = Poset([[1,2],[3],[3],[]])
sage: P.is_meet_semilattice()
True
sage: P = Poset({0:[2,3],1:[2,3]})
sage: P.is_meet_semilattice()
False
Returns True if the poset is ranked, and False otherwise.
A poset is {ranked} if it admits a rank function.
EXAMPLES:
sage: P = Poset([[1],[2],[3],[4],[]])
sage: P.is_ranked()
True
sage: Q = Poset([[1,5],[2,6],[3],[4],[],[6,3],[4]])
sage: Q.is_ranked()
False
Returns a matrix whose (i,j) entry is k, where self.linear_extension()[k] is the join (least upper bound) of self.linear_extension()[i] and self.linear_extension()[j].
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: J = P.join_matrix(); J
[0 1 2 3 4 5 6 7]
[1 1 3 3 7 7 7 7]
[2 3 2 3 4 6 6 7]
[3 3 3 3 7 7 7 7]
[4 7 4 7 4 7 7 7]
[5 7 6 7 7 5 6 7]
[6 7 6 7 7 6 6 7]
[7 7 7 7 7 7 7 7]
sage: J[P(4).vertex,P(3).vertex] == P(7).vertex
True
sage: J[P(5).vertex,P(2).vertex] == P(5).vertex
True
sage: J[P(5).vertex,P(2).vertex] == P(2).vertex
False
Computes the matrix whose [i,j] entry is 1 if self.linear_extension()[i] self.linear_extension()[j] 0 otherwise.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: LEQM = P.lequal_matrix(); LEQM
[1 1 1 1 1 1 1 1]
[0 1 0 1 0 0 0 1]
[0 0 1 1 1 0 1 1]
[0 0 0 1 0 0 0 1]
[0 0 0 0 1 0 0 1]
[0 0 0 0 0 1 1 1]
[0 0 0 0 0 0 1 1]
[0 0 0 0 0 0 0 1]
sage: LEQM[1,3]
1
sage: P.linear_extension()[1] < P.linear_extension()[3]
True
sage: LEQM[2,5]
0
sage: P.linear_extension()[2] < P.linear_extension()[5]
False
Returns a list l such that l[i+1] is the set of minimal elements of the poset obtained by removing the elements in l[0], l[1], ..., l[i].
EXAMPLES:
sage: P = Poset({0:[1,2],1:[3],2:[3],3:[]})
sage: [len(x) for x in P.level_sets()]
[1, 2, 1]
sage: Q = Poset({0:[1,2], 1:[3], 2:[4], 3:[4]})
sage: [len(x) for x in Q.level_sets()]
[1, 2, 1, 1]
Returns a linear extension of the poset.
EXAMPLES:
sage: B = Posets.BooleanLattice(3)
sage: B.linear_extension()
[0, 1, 2, 3, 4, 5, 6, 7]
Returns a list of all the linear extensions of the poset.
EXAMPLES:
sage: D = Poset({ 0:[1,2], 1:[3], 2:[3,4] })
sage: D.linear_extensions()
[[0, 1, 2, 3, 4], [0, 1, 2, 4, 3], [0, 2, 1, 3, 4], [0, 2, 1, 4, 3], [0, 2, 4, 1, 3]]
List the elements of the poset. This just returns the result of linear_extension().
EXAMPLES:
sage: D = Poset({ 0:[1,2], 1:[3], 2:[3,4] })
sage: D.list()
[0, 1, 2, 3, 4]
sage: type(D.list()[0])
<class 'sage.combinat.posets.elements.PosetElement'>
Returns a list of lower covers of the element y. An lower cover of y is an element x such that y x is a cover relation.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: map(Q.lower_covers,Q.list())
[[], [], [1, 0], [2], [3]]
Returns an iterator for the lower covers of the element y. An lower cover of y is an element x such that y x is a cover relation.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: type(Q.lower_covers_iterator(0))
<type 'generator'>
Returns a list of the maximal elements of the poset.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P.maximal_elements()
[4]
Returns a matrix whose (i,j) entry is k, where self.linear_extension()[k] is the meet (greatest lower bound) of self.linear_extension()[i] and self.linear_extension()[j].
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: M = P.meet_matrix(); M
[0 0 0 0 0 0 0 0]
[0 1 0 1 0 0 0 1]
[0 0 2 2 2 0 2 2]
[0 1 2 3 2 0 2 3]
[0 0 2 2 4 0 2 4]
[0 0 0 0 0 5 5 5]
[0 0 2 2 2 5 6 6]
[0 1 2 3 4 5 6 7]
sage: M[P(4).vertex,P(3).vertex] == P(0).vertex
True
sage: M[P(5).vertex,P(2).vertex] == P(2).vertex
True
sage: M[P(5).vertex,P(2).vertex] == P(5).vertex
False
Returns a list of the minimal elements of the poset.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P(0) in P.minimal_elements()
True
sage: P(1) in P.minimal_elements()
True
sage: P(2) in P.minimal_elements()
True
Returns the value of the Mobius function of the poset on the elements x and y.
EXAMPLES:
sage: P = Poset([[1,2,3],[4],[4],[4],[]])
sage: P.mobius_function(P(0),P(4))
2
sage: sum([P.mobius_function(P(0),v) for v in P])
0
sage: sum([abs(P.mobius_function(P(0),v)) \
... for v in P])
6
sage: for u,v in P.cover_relations_iterator():
... if P.mobius_function(u,v) != -1:
... print "Bug in mobius_function!"
sage: Q = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: Q.mobius_function(Q(0),Q(-1))
0
sage: Q.mobius_function(Q(0),Q(5))
0
sage: Q.mobius_function(Q(2),Q(7))
2
sage: Q.mobius_function(Q(3),Q(3))
1
sage: sum([Q.mobius_function(Q(0),v) for v in Q])
0
Returns a matrix whose (i,j) entry is the value of the Mobius function evaluated at self.linear_extension()[i] and self.linear_extension()[j].
EXAMPLES:
sage: P = Poset([[4,2,3],[],[1],[1],[1]])
sage: x,y = (P.linear_extension()[0],P.linear_extension()[1])
sage: P.mobius_function(x,y)
-1
sage: M = P.mobius_function_matrix(); M
[ 1 -1 -1 -1 2]
[ 0 1 0 0 -1]
[ 0 0 1 0 -1]
[ 0 0 0 1 -1]
[ 0 0 0 0 1]
sage: M[0,4]
2
sage: M[0,1]
-1
Returns a list of the elements  such that
such that 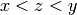 . The
order is that induced by the ordering in
self.linear_extension().
. The
order is that induced by the ordering in
self.linear_extension().
EXAMPLES:
sage: uc = [[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]]
sage: dag = DiGraph(dict(zip(range(len(uc)),uc)))
sage: P = Poset(dag)
sage: I = set(map(P,[5,6,4]))
sage: I == set(P.open_interval(2,7))
True
sage: dg = DiGraph({"a":["b","c"], "b":["d"], "c":["d"]})
sage: P = Poset(dg)
sage: P.open_interval("a","d")
[c, b]
Returns the order complex associated to this poset.
The order complex is the simplicial complex with vertices equal to the elements of the poset, and faces given by the chains.
EXAMPLES:
sage: P = Posets.BooleanLattice(3)
sage: S = P.order_complex(); S
Simplicial complex with vertex set (0, 1, 2, 3, 4, 5, 6, 7) and 6 facets
sage: S.f_vector()
[1, 8, 19, 18, 6]
sage: S.homology() # S is contractible
{0: 0, 1: 0, 2: 0, 3: 0}
sage: Q = P.subposet([1,2,3,4,5,6])
sage: Q.order_complex().homology() # a circle
{0: 0, 1: Z}
Returns the order filter generated by a list of elements.
 is an order filter if, for any
is an order filter if, for any  in
in  and
and  such that
such that
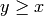 , then
, then  is in
is in  .
.
EXAMPLES:
sage: B = Posets.BooleanLattice(4)
sage: B.order_filter([3,8])
[8, 9, 10, 3, 11, 12, 13, 14, 7, 15]
Returns the order ideal generated by a list of elements.
 is an order ideal if, for any
is an order ideal if, for any  in
in  and
and  such that
such that
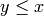 , then
, then  is in
is in  .
.
EXAMPLES:
sage: B = Posets.BooleanLattice(4)
sage: B.order_ideal([7,10])
[0, 8, 1, 2, 10, 3, 4, 5, 6, 7]
Returns a Graphic object corresponding the Hasse diagram of the poset. Optionally, it is labelled.
INPUT:
EXAMPLES:
sage: D = Poset({ 0:[1,2], 1:[3], 2:[3,4] })
sage: D.plot(label_elements=False)
sage: D.plot()
sage: type(D.plot())
<class 'sage.plot.plot.Graphics'>
sage: elm_labs = {0:'a', 1:'b', 2:'c', 3:'d', 4:'e'}
sage: D.plot(element_labels=elm_labs)
sage: P = Poset({})
sage: P.plot()
sage: P = Poset(DiGraph('E@ACA@?'))
sage: P.plot()
Returns the order filter generated by an element `x.
EXAMPLES:
sage: B = Posets.BooleanLattice(4)
sage: B.principal_order_filter(2)
[2, 10, 3, 11, 6, 14, 7, 15]
Returns the order ideal generated by an element x.
EXAMPLES:
sage: B = Posets.BooleanLattice(4)
sage: B.principal_order_ideal(6)
[0, 2, 4, 6]
Returns a random subposet that contains each element with probability p.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: Q = P.random_subposet(.25)
Returns the rank of an element, or the rank of the poset if element is None. (The rank of a poset is the length of the longest chain of elements of the poset.)
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: P.rank(5)
2
sage: P.rank()
3
sage: Q = Poset([[1,2],[3],[],[]])
sage: P = Posets.SymmetricGroupBruhatOrderPoset(4)
sage: [(v,P.rank(v)) for v in P]
[(1234, 0),
(1243, 1),
...
(4312, 5),
(4321, 6)]
Returns a rank function of the poset, if it exists.
A rank function of a poset  is a function
is a function  from that maps elements of
from that maps elements of  to integers and satisfies:
to integers and satisfies:
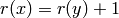 if
if  covers
covers
 .
.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: P.rank_function() is not None
True
sage: r = P.rank_function()
sage: for u,v in P.cover_relations_iterator():
... if r(v) != r(u) + 1:
... print "Bug in rank_function!"
sage: Q = Poset([[1,2],[4],[3],[4],[]])
sage: Q.rank_function() is None
True
Shows the Graphics object corresponding the Hasse diagram of the poset. Optionally, it is labelled.
INPUT:
EXAMPLES:
sage: D = Poset({ 0:[1,2], 1:[3], 2:[3,4] })
sage: D.plot(label_elements=False)
sage: D.show()
sage: elm_labs = {0:'a', 1:'b', 2:'c', 3:'d', 4:'e'}
sage: D.show(element_labels=elm_labs)
Returns the number of elements in the poset.
EXAMPLES:
sage: Poset([[1,2,3],[4],[4],[4],[]]).cardinality()
5
Returns the poset containing elements with partial order induced by that of self.
EXAMPLES:
sage: P = Poset({"a":["c","d"], "b":["d","e"], "c":["f"], "d":["f"], "e":["f"]})
sage: P.subposet(["a","b","f"])
Finite poset containing 3 elements
sage: P = posets.BooleanLattice(2)
sage: above = P.principal_order_filter(0)
sage: Q = P.subposet(above)
sage: above_new = Q.principal_order_filter(Q.list()[0])
sage: Q.subposet(above_new)
Finite poset containing 4 elements
Returns the top element of the poset, if it exists.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4,5],4:[],5:[]})
sage: P.top() is None
True
sage: Q = Poset({0:[1],1:[]})
sage: Q.top()
1
Returns a list of upper covers of the element y. An upper cover of y is an element x such that y x is a cover relation.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: map(Q.upper_covers,Q.list())
[[2], [2], [3], [4], []]
Returns an iterator for the upper covers of the element y. An upper cover of y is an element x such that y x is a cover relation.
EXAMPLES:
sage: Q = Poset({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: type(Q.upper_covers_iterator(0))
<type 'generator'>
Bases: sage.combinat.combinat.CombinatorialClass
The Combinatorial Class of all posets on  vertices.
vertices.
Return the cardinality of this object.
Note
By default, this returns pre-computed values obtained from the On-Line Encyclopedia of Integer Sequences (A000112). To override this, use pass the argument from_iterator=True.
EXAMPLES:
sage: P = Posets(3)
sage: P.cardinality()
5
sage: P.cardinality(from_iterator=True)
5
Construct a poset from various forms of input data.
INPUT:
A two-element list or tuple (E, R), where E is a collection of elements of the poset and R is the set of relations. Elements of R are two-element lists/tuples/iterables. If cover_relations=True, then R is assumed to be the cover relations of the poset. If E is empty, then E is taken to be the set of elements appearing in the relations R.
A two-element list or tuple (E, f), where E is the set of elements of the poset and f is a function such that f(x,y) is True if x <= y and False otherwise for all pairs of elements in E. If cover_relations=True, then f(x,y) should be True if and only if x is covered by y, and False otherwise.
A dictionary, list or tuple of upper covers: data[x] is an list of the elements that cover the element x in the poset.
Note
If data is a list or tuple of length 2, then it is handled by the above cases.
An acyclic, loop-free and multi-edge free DiGraph. If cover_relations is True, then the edges of the digraph correspond to cover relations in the poset. If cover_relations is False, then the cover relations are computed.
A previously constructed poset (the poset itself is returned).
OUTPUT:
FinitePoset – an instance of the FinitePoset class.
EXAMPLES:
Elements and cover relations:
sage: elms = [1,2,3,4,5,6,7]
sage: rels = [[1,2],[3,4],[4,5],[2,5]]
sage: Poset((elms, rels), cover_relations = True)
Finite poset containing 7 elements
Elements and non-cover relations:
sage: elms = [1,2,3,4]
sage: rels = [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
sage: P = Poset( [elms,rels] ,cover_relations=False); P
Finite poset containing 4 elements
sage: P.cover_relations()
[[1, 2], [2, 3], [3, 4]]
Elements and function: the standard permutations of [1, 2, 3, 4] with the Bruhat order:
sage: elms = Permutations(4)
sage: fcn = lambda p,q : p.bruhat_lequal(q)
sage: Poset((elms, fcn))
Finite poset containing 24 elements
With a function that identifies the cover relations: the set partitions of {1, 2, 3} ordered by refinement:
sage: elms = SetPartitions(3)
sage: def fcn(A, B):
... if len(A) != len(B)+1:
... return False
... for a in A:
... if not any(set(a).issubset(b) for b in B):
... return False
... return True
sage: Poset((elms, fcn), cover_relations=True)
Finite poset containing 5 elements
A dictionary of upper covers:
sage: Poset({'a':['b','c'], 'b':['d'], 'c':['d'], 'd':[]})
Finite poset containing 4 elements
A list of upper covers:
sage: Poset([[1,2],[4],[3],[4],[]])
Finite poset containing 5 elements
A list of upper covers and a dictionary of labels:
sage: elm_labs = {0:"a",1:"b",2:"c",3:"d",4:"e"}
sage: P = Poset([[1,2],[4],[3],[4],[]],elm_labs)
sage: P.list()
[a, b, c, d, e]
Warning
The special case where the argument data is a list or tuple of length 2 is handled by the above cases. So you cannot use this method to input a 2-element poset.
An acyclic DiGraph.
sage: dag = DiGraph({0:[2,3], 1:[3,4], 2:[5], 3:[5], 4:[5]})
sage: Poset(dag)
Finite poset containing 6 elements
Any directed acyclic graph without loops or multiple edges, as long as cover_relations=False:
sage: dig = DiGraph({0:[2,3], 1:[3,4,5], 2:[5], 3:[5], 4:[5]})
sage: dig.allows_multiple_edges()
False
sage: dig.allows_loops()
False
sage: dig.transitive_reduction() == dig
False
sage: Poset(dig, cover_relations=False)
Finite poset containing 6 elements
sage: Poset(dig, cover_relations=True)
...
ValueError: Hasse diagram is not transitively reduced.
Bases: sage.combinat.combinat.InfiniteAbstractCombinatorialClass
The Combinatorial Class of all posets.
Tests whether a directed graph is acyclic and transitively reduced.
EXAMPLES:
sage: from sage.combinat.posets.posets import is_poset
sage: dig = DiGraph({0:[2,3], 1:[3,4,5], 2:[5], 3:[5], 4:[5]})
sage: is_poset(dig)
False
sage: is_poset(dig.transitive_reduction())
True