Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »
- Posets »

Bases: sage.graphs.digraph.DiGraph
The Hasse diagram of a poset. This is just a transitively-reduced, directed, acyclic graph without loops or multiple edges.
Note
We assume that range(n) is a linear extension of the poset. That is, range(n) is the vertex set and a topological sort of the digraph.
This should not be called directly, use Poset instead; all type checking happens there.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[]}); H
Hasse diagram of a poset containing 4 elements
sage: H == loads(dumps(H))
True
Returns a list of all antichains of the poset.
An antichain of a poset is a collection of elements of the poset that are pairwise incomparable.
Note
This algorithm is based on Freese-Jezek-Nation p226
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2],1:[4],2:[3],3:[4]})
sage: H.antichains()
[[], [0], [1], [2], [3], [4], [1, 2], [1, 3]]
sage: H = HasseDiagram({0:[],1:[],2:[]})
sage: H.antichains()
[[], [0], [1], [2], [1, 2], [0, 1], [0, 2], [0, 1, 2]]
sage: H = HasseDiagram({0:[1],1:[2],2:[3],3:[4]})
sage: H.antichains()
[[], [0], [1], [2], [3], [4]]
Returns the bottom element of the poset, if it exists.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P.bottom() is None
True
sage: Q = Poset({0:[1],1:[]})
sage: Q.bottom()
0
Returns the number of elements in the poset.
EXAMPLES:
sage: Poset([[1,2,3],[4],[4],[4],[]]).cardinality()
5
Returns a list of the elements z such that x = z = y. The order is that induced by the ordering in self.linear_extension.
EXAMPLES:
sage: uc = [[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]]
sage: dag = DiGraph(dict(zip(range(len(uc)),uc)))
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram(dag)
sage: set([2,5,6,4,7]) == set(H.closed_interval(2,7))
True
Returns a list l such that l[i] is a complement of i in self.
A complement of x is an element y such that the meet of x and y is the bottom element of self and the join of x and y is the top element of self.
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram sage: H = HasseDiagram({0:[1,2,3],1:[4],2:[4],3:[4]}) sage: H.complements() [4, 3, 3, 2, 0]
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[4]}) sage: H.complements() [4, None, None, None, 0]
Returns True if y covers x and False otherwise.
EXAMPLES:
sage: Q = Poset([[1,5],[2,6],[3],[4],[],[6,3],[4]])
sage: Q.covers(Q(1),Q(6))
True
sage: Q.covers(Q(1),Q(4))
False
Create an aliased version of a function or a method which raise a deprecation warning message.
If f is a function or a method, write g = deprecated_function_alias(f, "Sage version") to make a deprecated aliased version of f.
INPUT:
- func - the function or method to be aliased
- version - the version of sage when the function is deprecated
EXAMPLES:
sage: from sage.misc.misc import deprecated_function_alias
sage: g = deprecated_function_alias(number_of_partitions,
... 'Sage Version 42.132')
sage: g(5)
doctest:...: DeprecationWarning: (Since Sage Version 42.132) g is deprecated. Please use number_of_partitions instead.
7
This also works for methods:
sage: class cls(object):
... def new_meth(self): return 42
... old_meth = deprecated_function_alias(new_meth,
... 'Sage Version 42.132')
sage: cls().old_meth()
doctest:...: DeprecationWarning: (Since Sage Version 42.132) old_meth is deprecated. Please use new_meth instead.
42
AUTHORS:
- Florent Hivert (2009-11-23), with the help of Mike Hansen.
Returns a poset that is dual to the given poset.
EXAMPLE:
sage: P = Poset([[1,2],[4],[3],[4],[]])
sage: P.dual()
Finite poset containing 5 elements
Returns True if the poset has a unique minimal element.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P.has_bottom()
False
sage: Q = Poset({0:[1],1:[]})
sage: Q.has_bottom()
True
Returns True if the poset contains a unique maximal element, and False otherwise.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4,5],4:[],5:[]})
sage: P.has_top()
False
sage: Q = Poset({0:[1],1:[]})
sage: Q.has_top()
True
Returns a list of the elements z such that x <= z <= y. The order is that induced by the ordering in self.linear_extension.
INPUT:
EXAMPLES:
sage: uc = [[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]]
sage: dag = DiGraph(dict(zip(range(len(uc)),uc)))
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram(dag)
sage: I = set([2,5,6,4,7])
sage: I == set(H.interval(2,7))
True
Returns True if the poset contains a unique maximal element and a unique minimal element, and False otherwise.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4,5],4:[],5:[]})
sage: P.is_bounded()
False
sage: Q = Poset({0:[1],1:[]})
sage: Q.is_bounded()
True
Returns True if the poset is totally ordered, and False otherwise.
EXAMPLES:
sage: L = Poset({0:[1],1:[2],2:[3],3:[4]})
sage: L.is_chain()
True
sage: V = Poset({0:[1,2]})
sage: V.is_chain()
False
Returns True if self is the Hasse diagram of a complemented lattice, and False otherwise.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2,3],1:[4],2:[4],3:[4]})
sage: H.is_complemented_lattice()
True
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[4]})
sage: H.is_complemented_lattice()
False
Returns True if self is the Hasse diagram of a distributive lattice, and False otherwise.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.is_distributive_lattice()
False
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3]})
sage: H.is_distributive_lattice()
True
sage: H = HasseDiagram({0:[1,2,3],1:[4],2:[4],3:[4]})
sage: H.is_distributive_lattice()
False
This function is deprecated and will be removed in a future version of Sage. Please use self.is_distributive_lattice() instead.
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.is_distributive_lattice_fastest()
doctest:1: DeprecationWarning: is_distributive_lattice_fastest is deprecated, use is_distributive_lattice instead!
False
Returns True if x is greater than or equal to y, and False otherwise.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: Q = HasseDiagram({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = 0,1,4
sage: Q.is_gequal(x,y)
False
sage: Q.is_gequal(y,x)
False
sage: Q.is_gequal(x,z)
False
sage: Q.is_gequal(z,x)
True
sage: Q.is_gequal(z,y)
True
sage: Q.is_gequal(z,z)
True
Returns True if the poset is graded, and False otherwise.
A poset is {graded} if it admits a rank function.
EXAMPLES:
sage: P = Poset([[1],[2],[3],[4],[]])
sage: P.is_graded()
True
sage: Q = Poset([[1,5],[2,6],[3],[4],[],[6,3],[4]])
sage: Q.is_graded()
False
Returns True if x is greater than but not equal to y, and False otherwise.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: Q = HasseDiagram({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = 0,1,4
sage: Q.is_greater_than(x,y)
False
sage: Q.is_greater_than(y,x)
False
sage: Q.is_greater_than(x,z)
False
sage: Q.is_greater_than(z,x)
True
sage: Q.is_greater_than(z,y)
True
sage: Q.is_greater_than(z,z)
False
Returns True if self has a join operation, and False otherwise.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.is_join_semilattice()
True
sage: H = HasseDiagram({0:[2,3],1:[2,3]})
sage: H.is_join_semilattice()
False
sage: H = HasseDiagram({0:[2,3],1:[2,3],2:[4],3:[4]})
sage: H.is_join_semilattice()
False
Returns True if i is less than or equal to j in the poset, and False otherwise.
Note
If the leq_matrix has been computed, then this method is redefined to use the cached matrix (see _alternate_is_lequal).
Returns True if x is less than or equal to y in the poset, and False otherwise.
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[2], 1:[2], 2:[3], 3:[4], 4:[]})
sage: x,y,z = 0, 1, 4
sage: H.is_less_than(x,y)
False
sage: H.is_less_than(y,x)
False
sage: H.is_less_than(x,z)
True
sage: H.is_less_than(y,z)
True
sage: H.is_less_than(z,z)
False
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[]})
sage: H.is_linear_extension(range(4))
True
sage: H.is_linear_extension([3,2,1,0])
False
Returns True if self has a meet operation, and False otherwise.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.is_meet_semilattice()
True
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[]})
sage: H.is_meet_semilattice()
True
sage: H = HasseDiagram({0:[2,3],1:[2,3]})
sage: H.is_meet_semilattice()
False
Returns True if the poset is ranked, and False otherwise.
A poset is ranked if it admits a rank function.
EXAMPLES:
sage: P = Poset([[1],[2],[3],[4],[]])
sage: P.is_ranked()
True
sage: Q = Poset([[1,5],[2,6],[3],[4],[],[6,3],[4]])
sage: Q.is_ranked()
False
Returns the matrix of joins of self. The (x,y)-entry of this matrix is the join of x and y in self.
This algorithm is modelled after the algorithm of Freese-Jezek-Nation (p217).
Note
Once the matrix has been computed, it is stored in self._join_matrix. Delete this attribute if you want to recompute the matrix.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.join_matrix()
[0 1 2 3 4 5 6 7]
[1 1 4 7 4 7 7 7]
[2 4 2 6 4 5 6 7]
[3 7 6 3 7 7 6 7]
[4 4 4 7 4 7 7 7]
[5 7 5 7 7 5 7 7]
[6 7 6 6 7 7 6 7]
[7 7 7 7 7 7 7 7]
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[2,3],1:[2,3]})
sage: H.join_matrix()
...
ValueError: Not a join-semilattice: no top element.
sage: H = HasseDiagram({0:[2,3],1:[2,3],2:[4],3:[4]})
sage: H.join_matrix()
...
ValueError: No join for x=...
Computes a matrix whose [i,j] entry is 1 if self.linear_extension[i] <= self.linear_extension[j] and 0 otherwise. The matrix is stored in the attribute _leq_matrix and the method __lt__ is redefined to use this matrix.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: H = P._hasse_diagram
sage: hasattr(H,'_leq_matrix')
False
sage: H.lequal_matrix()
[1 1 1 1 1 1 1 1]
[0 1 0 1 0 0 0 1]
[0 0 1 1 1 0 1 1]
[0 0 0 1 0 0 0 1]
[0 0 0 0 1 0 0 1]
[0 0 0 0 0 1 1 1]
[0 0 0 0 0 0 1 1]
[0 0 0 0 0 0 0 1]
sage: hasattr(H,'_leq_matrix')
True
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[]})
sage: H.linear_extension()
[0, 1, 2, 3]
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[]})
sage: H.linear_extensions()
[[0, 1, 2, 3], [0, 2, 1, 3]]
Returns the list of elements that are covered by element.
Returns a list of the maximal elements of the poset.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P.maximal_elements()
[4]
Returns the matrix of meets of self. The (x,y)-entry of this matrix is the meet of x and y in self.
This algorithm is modelled after the algorithm of Freese-Jezek-Nation (p217).
Note
Once the matrix has been computed, it is stored in self._meet_matrix. Delete this attribute if you want to recompute the matrix.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.meet_matrix()
[0 0 0 0 0 0 0 0]
[0 1 0 0 1 0 0 1]
[0 0 2 0 2 2 2 2]
[0 0 0 3 0 0 3 3]
[0 1 2 0 4 2 2 4]
[0 0 2 0 2 5 2 5]
[0 0 2 3 2 2 6 6]
[0 1 2 3 4 5 6 7]
TESTS:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[2,3],1:[2,3]})
sage: H.meet_matrix()
...
ValueError: Not a meet-semilattice: no bottom element.
sage: H = HasseDiagram({0:[1,2],1:[3,4],2:[3,4]})
sage: H.meet_matrix()
...
ValueError: No meet for x=...
Returns a list of the minimal elements of the poset.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4],4:[]})
sage: P(0) in P.minimal_elements()
True
sage: P(1) in P.minimal_elements()
True
sage: P(2) in P.minimal_elements()
True
Returns the value of the M”obius function of the poset on the elements i and j.
EXAMPLES:
sage: P = Poset([[1,2,3],[4],[4],[4],[]])
sage: H = P._hasse_diagram
sage: H.mobius_function(0,4)
2
sage: for u,v in P.cover_relations_iterator():
... if P.mobius_function(u,v) != -1:
... print "Bug in mobius_function!"
Returns a matrix whose (x, y) entry is the value of the M”obius function of self evaluated on x and y.
Note
Once this matrix has been computed, it is stored in self._mobius_function_matrix. Delete this attribute if you want to recompute the matrix.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.mobius_function_matrix()
[ 1 -1 -1 -1 1 0 1 0]
[ 0 1 0 0 -1 0 0 0]
[ 0 0 1 0 -1 -1 -1 2]
[ 0 0 0 1 0 0 -1 0]
[ 0 0 0 0 1 0 0 -1]
[ 0 0 0 0 0 1 0 -1]
[ 0 0 0 0 0 0 1 -1]
[ 0 0 0 0 0 0 0 1]
sage: hasattr(H,'_mobius_function_matrix')
True
Returns a list of the elements  such that
such that 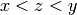 . The
order is that induced by the ordering in
self.linear_extension.
. The
order is that induced by the ordering in
self.linear_extension.
EXAMPLES:
sage: uc = [[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]]
sage: dag = DiGraph(dict(zip(range(len(uc)),uc)))
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram(dag)
sage: set([5,6,4]) == set(H.open_interval(2,7))
True
sage: H.open_interval(7,2)
[]
Returns the order filter generated by a list of elements.
 is an order filter if, for any
is an order filter if, for any  in
in  and
and  such that
such that
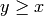 , then
, then  is in
is in  .
.
EXAMPLES:
sage: H = Posets.BooleanLattice(4)._hasse_diagram
sage: H.order_filter([3,8])
[3, 7, 8, 9, 10, 11, 12, 13, 14, 15]
Returns the order ideal generated by a list of elements.
 is an order ideal if, for any
is an order ideal if, for any  in
in  and
and  such that
such that
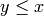 , then
, then  is in
is in  .
.
EXAMPLES:
sage: H = Posets.BooleanLattice(4)._hasse_diagram
sage: H.order_ideal([7,10])
[0, 1, 2, 3, 4, 5, 6, 7, 8, 10]
Returns a Graphics object corresponding to the Hasse diagram.
EXAMPLES:
sage: uc = [[2,3], [], [1], [1], [1], [3,4]]
sage: elm_lbls = Permutations(3).list()
sage: P = Poset(uc,elm_lbls)
sage: H = P._hasse_diagram
sage: levels = H.level_sets()
sage: heights = dict([[i, levels[i]] for i in range(len(levels))])
sage: type(H.plot(label_elements=True))
<class 'sage.plot.plot.Graphics'>
sage: P = Posets.SymmetricGroupBruhatIntervalPoset([0,1,2,3], [2,3,0,1])
sage: P._hasse_diagram.plot()
Returns the order filter generated by i.
EXAMPLES:
sage: H = Posets.BooleanLattice(4)._hasse_diagram
sage: H.principal_order_filter(2)
[2, 3, 6, 7, 10, 11, 14, 15]
Returns the order ideal generated by  .
.
EXAMPLES:
sage: H = Posets.BooleanLattice(4)._hasse_diagram
sage: H.principal_order_ideal(6)
[0, 2, 4, 6]
Returns the rank of element, or the rank of the poset if element is None. (The rank of a poset is the length of the longest chain of elements of the poset.)
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: H.rank(5)
2
sage: H.rank()
3
sage: Q = HasseDiagram({0:[1,2],1:[3],2:[],3:[]})
sage: Q.rank()
2
sage: Q.rank(1)
1
Returns a rank function of the poset, if it exists.
A rank function of a poset  is a function
is a function  from that maps elements of
from that maps elements of  to integers and satisfies:
to integers and satisfies:
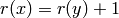 if
if  covers
covers
 .
.
EXAMPLES:
sage: P = Poset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]])
sage: P.rank_function() is not None
True
sage: r = P.rank_function()
sage: for u,v in P.cover_relations_iterator():
... if r(v) != r(u) + 1:
... print "Bug in rank_function!"
sage: Q = Poset([[1,2],[4],[3],[4],[]])
sage: Q.rank_function() is None
True
Shows the Graphics object corresponding to the Hasse diagram. Optionally, it is labelled.
INPUT:
EXAMPLES:
sage: uc = [[2,3], [], [1], [1], [1], [3,4]]
sage: elm_lbls = Permutations(3).list()
sage: P = Poset(uc,elm_lbls)
sage: H = P._hasse_diagram
sage: levels = H.level_sets()
sage: heights = dict([[i, levels[i]] for i in range(len(levels))])
sage: H.show(label_elements=True)
Returns the number of elements in the poset.
EXAMPLES:
sage: Poset([[1,2,3],[4],[4],[4],[]]).cardinality()
5
Returns the top element of the poset, if it exists.
EXAMPLES:
sage: P = Poset({0:[3],1:[3],2:[3],3:[4,5],4:[],5:[]})
sage: P.top() is None
True
sage: Q = Poset({0:[1],1:[]})
sage: Q.top()
1
Returns the list of elements that cover element.
EXAMPLES:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,3,2],1:[4],2:[4,5,6],3:[6],4:[7],5:[7],6:[7],7:[]})
sage: list(H.upper_covers_iterator(0))
[1, 2, 3]
sage: list(H.upper_covers_iterator(7))
[]