Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »

AUTHORS:
- Mike Hanson (2007) - original module
- Nathann Cohen, David Joyner (2009-2010) - Gale-Ryser stuff
Returns the combinatorial class of integer vectors.
EXAMPLES: If n is not specified, it returns the class of all integer vectors.
sage: IntegerVectors()
Integer vectors
sage: [] in IntegerVectors()
True
sage: [1,2,1] in IntegerVectors()
True
sage: [1, 0, 0] in IntegerVectors()
True
If n is specified, then it returns the class of all integer vectors which sum to n.
sage: IV3 = IntegerVectors(3); IV3
Integer vectors that sum to 3
Note that trailing zeros are ignored so that [3, 0] does not show up in the following list (since [3] does)
sage: IntegerVectors(3, max_length=2).list()
[[3], [2, 1], [1, 2], [0, 3]]
If n and k are both specified, then it returns the class of integer vectors that sum to n and are of length k.
sage: IV53 = IntegerVectors(5,3); IV53
Integer vectors of length 3 that sum to 5
sage: IV53.cardinality()
21
sage: IV53.first()
[5, 0, 0]
sage: IV53.last()
[0, 0, 5]
sage: IV53.random_element()
[4, 0, 1]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: IntegerVectors().cardinality()
+Infinity
EXAMPLES:
sage: IntegerVectors().list()
...
NotImplementedError: infinite list
Bases: sage.combinat.integer_vector.IntegerVectors_nkconstraints
EXAMPLES:
sage: IntegerVectors(3, max_length=2).cardinality()
4
sage: IntegerVectors(3).cardinality()
+Infinity
EXAMPLES:
sage: IntegerVectors(3, max_length=2).list()
[[3], [2, 1], [1, 2], [0, 3]]
sage: IntegerVectors(3).list()
...
NotImplementedError: infinite list
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLE:
sage: IV = IntegerVectors(2,3)
sage: IV.list()
[[2, 0, 0], [1, 1, 0], [1, 0, 1], [0, 2, 0], [0, 1, 1], [0, 0, 2]]
sage: IntegerVectors(3, 0).list()
[]
sage: IntegerVectors(3, 1).list()
[[3]]
sage: IntegerVectors(0, 1).list()
[[0]]
sage: IntegerVectors(0, 2).list()
[[0, 0]]
sage: IntegerVectors(2, 2).list()
[[2, 0], [1, 1], [0, 2]]
Bases: sage.combinat.combinat.CombinatorialClass
EXAMPLES:
sage: IntegerVectors(3,3, min_part=1).cardinality()
1
sage: IntegerVectors(5,3, min_part=1).cardinality()
6
sage: IntegerVectors(13, 4, min_part=2, max_part=4).cardinality()
16
EXAMPLES:
sage: IntegerVectors(2,3,min_slope=0).first()
[0, 1, 1]
EXAMPLES:
sage: IntegerVectors(2,3,min_slope=0).last()
[0, 0, 2]
Bases: sage.combinat.combinat.CombinatorialClass
The combinatorial class of integer vectors v graded by two parameters:
In other words: the length of v equals c[1]+...+c[k], and v is decreasing in the consecutive blocs of length c[1], ..., c[k]
Those are the integer vectors of sum n which are lexicographically maximal (for the natural left->right reading) in their orbit by the young subgroup S_c_1 x x S_c_k. In particular, they form a set of orbit representative of integer vectors w.r.t. this young subgroup.
Returns the constant function i.
EXAMPLES:
sage: f = sage.combinat.integer_vector.constant_func(3)
sage: f(-1)
3
sage: f('asf')
3
Returns the binary matrix given by the Gale-Ryser theorem.
The Gale Ryser theorem asserts that if 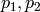 are two
partitions of
are two
partitions of  of respective lengths
of respective lengths 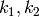 , then there is
a binary
, then there is
a binary 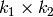 matrix
matrix  such that
such that 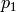 is the vector
of row sums and
is the vector
of row sums and 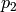 is the vector of column sums of
is the vector of column sums of  , if
and only if the conjugate of
, if
and only if the conjugate of 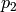 dominates
dominates 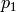 .
.
INPUT:
p1, p2– list of integers representing the vectors of row/column sums
algorithm – two possible string values :
OUTPUT:
Gale’s Algorithm:
(Gale [Gale57]): A matrix satisfying the constraints of its sums can be defined as the solution of the following Linear Program, which Sage knows how to solve (requires packages GLPK or CBC).
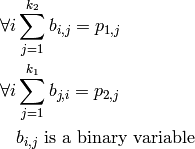
Ryser’s Algorithm:
(Ryser [Ryser63]): The construction of an 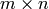 matrix
matrix 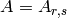 ,
due to Ryser, is described as follows. The
construction works if and only if have
,
due to Ryser, is described as follows. The
construction works if and only if have 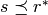 .
.
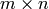 matrix
matrix  from
from  by defining
the
by defining
the  -th row of
-th row of  to be the vector whose first
to be the vector whose first 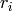 entries are
entries are  , and the remainder are 0’s,
, and the remainder are 0’s, 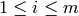 . This maximal matrix
. This maximal matrix  with row sum
with row sum  and ones left
justified has column sum
and ones left
justified has column sum 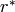 .
. in certain rows of
in certain rows of  to column
to column  in
order to achieve the sum
in
order to achieve the sum 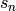 . Call this
. Call this  again.
again. ‘s in column n are to appear in those
rows in which
‘s in column n are to appear in those
rows in which  has the largest row sums, giving
preference to the bottom-most positions in case of ties.
has the largest row sums, giving
preference to the bottom-most positions in case of ties.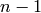 , ...,
, ...,  ,
,  .
.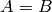 . Return
. Return  .
.EXAMPLES:
Computing the matrix for 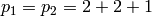
sage: from sage.combinat.integer_vector import gale_ryser_theorem
sage: p1 = [2,2,1]
sage: p2 = [2,2,1]
sage: print gale_ryser_theorem(p1, p2, algorithm="gale") # Optional - requires GLPK or CBC
[0 1 1]
[1 1 0]
[1 0 0]
Or for a non-square matrix with 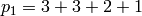 and
and 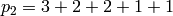
sage: from sage.combinat.integer_vector import gale_ryser_theorem
sage: p1 = [3,3,1,1]
sage: p2 = [3,3,1,1]
sage: gale_ryser_theorem(p1, p2)
[1 1 1 0]
[1 1 0 1]
[1 0 0 0]
[0 1 0 0]
sage: p1 = [4,2,2]
sage: p2 = [3,3,1,1]
sage: gale_ryser_theorem(p1, p2)
[1 1 1 1]
[1 1 0 0]
[1 1 0 0]
sage: p1 = [4,2,2,0]
sage: p2 = [3,3,1,1,0,0]
sage: gale_ryser_theorem(p1, p2)
[1 1 1 1 0 0]
[1 1 0 0 0 0]
[1 1 0 0 0 0]
[0 0 0 0 0 0]
sage: p1 = [3,3,2,1]
sage: p2 = [3,2,2,1,1]
sage: print gale_ryser_theorem(p1, p2, algorithm="gale") # Optional - requires GLPK or CBC
[1 0 1 1 0]
[1 0 1 0 1]
[1 1 0 0 0]
[0 1 0 0 0]
With  in the sequences, and with unordered inputs
in the sequences, and with unordered inputs
sage: from sage.combinat.integer_vector import gale_ryser_theorem
sage: gale_ryser_theorem([3,3,0,1,1,0], [3,1,3,1,0])
[1 1 1 0 0]
[1 0 1 1 0]
[0 0 0 0 0]
[1 0 0 0 0]
[0 0 1 0 0]
[0 0 0 0 0]
REFERENCES:
| [Ryser63] | (1, 2) H. J. Ryser, Combinatorial Mathematics, Carus Monographs, MAA, 1963. |
| [Gale57] | (1, 2) D. Gale, A theorem on flows in networks, Pacific J. Math. 7(1957)1073-1082. |
Tests whether the given sequences satisfy the condition of the Gale-Ryser theorem.
Given a binary matrix  of dimension
of dimension 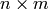 , the
vector of row sums is defined as the vector whose
, the
vector of row sums is defined as the vector whose
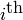 component is equal to the sum of the
component is equal to the sum of the 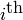 row in
row in  . The vector of column sums is defined similarly.
. The vector of column sums is defined similarly.
If, given a binary matrix, these two vectors are easy to compute,
the Gale-Ryser theorem lets us decide whether, given two
non-negative vectors 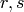 , there exists a binary matrix
whose row/colum sums vectors are
, there exists a binary matrix
whose row/colum sums vectors are  and
and  .
.
This functions answers accordingly.
INPUT:
ALGORITHM:
Without loss of generality, we can assume that:
 ( which would
correspond to an empty column/row )
( which would
correspond to an empty column/row )We can then assume that  and
and  are partitions
(see the corresponding class Partition)
are partitions
(see the corresponding class Partition)
If 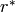 denote the conjugate of
denote the conjugate of  , the Gale-Ryser theorem
asserts that a binary Matrix satisfying the constraints exists
if and only if
, the Gale-Ryser theorem
asserts that a binary Matrix satisfying the constraints exists
if and only if 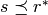 , where
, where 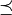 denotes
the domination order on partitions.
denotes
the domination order on partitions.
EXAMPLES:
sage: from sage.combinat.integer_vector import is_gale_ryser
sage: is_gale_ryser([4,2,2],[3,3,1,1])
True
sage: is_gale_ryser([4,2,1,1],[3,3,1,1])
True
sage: is_gale_ryser([3,2,1,1],[3,3,1,1])
False
REMARK: In the literature, what we are calling a Gale-Ryser sequence sometimes goes by the (rather generic-sounding) term ‘’realizable sequence’‘.
Given a list l, return a function that takes in a value i and return l[i-1]. If default is not None, then the function will return the default value for out of range i’s.
EXAMPLES:
sage: f = sage.combinat.integer_vector.list2func([1,2,3])
sage: f(1)
1
sage: f(2)
2
sage: f(3)
3
sage: f(4)
...
IndexError: list index out of range
sage: f = sage.combinat.integer_vector.list2func([1,2,3], 0)
sage: f(3)
3
sage: f(4)
0