Free modules

class sage.combinat.free_module.CartesianProductWithFlattening(flatten)

Bases: object

A class for cartesian product constructor, with partial flattening

class sage.combinat.free_module.CombinatorialFreeModule(R, basis_keys, element_class=None, prefix='B', category=None)

Bases: sage.structure.unique_representation.UniqueRepresentation, sage.modules.module.Module

EXAMPLES:

We construct a free module whose basis is indexed by the letters a, b, c:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: F
Free module generated by {'a', 'b', 'c'} over Rational Field

Its basis is a family, indexed by a, b, c:

sage: e = F.basis()
sage: e
Finite family {'a': B['a'], 'c': B['c'], 'b': B['b']}

sage: [x for x in e]
[B['a'], B['b'], B['c']]
sage: [k for k in e.keys()]
['a', 'b', 'c']

Let us construct some elements, and compute with them:

sage: e['a']
B['a']
sage: 2*e['a']
2*B['a']
sage: e['a'] + 3*e['b']
B['a'] + 3*B['b']

Some uses of summation() and sum():

sage: F = CombinatorialFreeModule(QQ, [1,2,3,4])
sage: F.summation(F.monomial(1), F.monomial(3))
B[1] + B[3]

sage: F = CombinatorialFreeModule(QQ, [1,2,3,4])
sage: F.sum(F.monomial(i) for i in [1,2,3])
B[1] + B[2] + B[3]

Note that the constructed free module depends on the order of the basis:

sage: F1 = CombinatorialFreeModule(QQ, (1,2,3,4))
sage: F1 is F
True
sage: F1 = CombinatorialFreeModule(QQ, [4,3,2,1])
sage: F1 == F
False

CartesianProduct

alias of CombinatorialFreeModule_CartesianProduct

Element

alias of CombinatorialFreeModuleElement

Tensor

alias of CombinatorialFreeModule_Tensor

basis()

Returns the basis of self.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: F.basis()
Finite family {'a': B['a'], 'c': B['c'], 'b': B['b']}

sage: QS3 = SymmetricGroupAlgebra(QQ,3)
sage: list(QS3.basis())
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

combinatorial_class()

Returns the combinatorial class that indexes the basis elements.

Deprecated: use self.basis().keys() instead.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.combinatorial_class()
doctest:...: DeprecationWarning: "FM.combinatorial_class()" is deprecated. Use "F.basis().keys()" instead !
{'a', 'b', 'c'}

sage: s = SFASchur(QQ)
sage: s.combinatorial_class()
Partitions

dimension()

Returns the dimension of the combinatorial algebra (which is given by the number of elements in the basis).

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.dimension()
3
sage: F.basis().cardinality()
3
sage: F.basis().keys().cardinality()
3

sage: s = SFASchur(QQ)
sage: s.dimension()
+Infinity

from_vector(vector)

Build an element of self from a (sparse) vector

See self.get_order and the method to_vector of the elements of self

EXAMPLES:

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: b = QS3.from_vector(vector((2, 0, 0, 0, 0, 4))); b
2*[1, 2, 3] + 4*[3, 2, 1]
sage: a = 2*QS3([1,2,3])+4*QS3([3,2,1])
sage: a == b
True

get_order()

Returns the order of the elements in the basis.

EXAMPLES:

sage: QS2 = SymmetricGroupAlgebra(QQ,2)
sage: QS2.get_order()                    # note: order changed on 2009-03-13
[[2, 1], [1, 2]]

monomial()

INPUT:

• ‘’i’‘

Returns the basis element indexed by i

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.monomial('a')
B['a']

F.monomial is in fact (almost) a map:

sage: F.monomial
Term map from {'a', 'b', 'c'} to Free module generated by {'a', 'b', 'c'} over Rational Field

monomial_or_zero_if_none(i)

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.monomial_or_zero_if_none('a')
B['a']
sage: F.monomial_or_zero_if_none(None)
0

prefix()

Returns the prefix used when displaying elements of self.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.prefix()
'B'

sage: X = SchubertPolynomialRing(QQ)
sage: X.prefix()
'X'

set_order(order)

Sets the order of the elements of the basis.

If set_order() has not been called, then the ordering is the one used in the generation of the elements of self’s associated enumerated set.

EXAMPLES:

sage: QS2 = SymmetricGroupAlgebra(QQ,2)
sage: b = list(QS2.basis().keys())
sage: b.reverse()
sage: QS2.set_order(b)
sage: QS2.get_order()
[[2, 1], [1, 2]]

sum_of_monomials()

INPUT:

• ‘’indices’’ – an list (or iterable) of indices of basis elements

Returns the sum of the corresponding basis elements

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.sum_of_monomials(['a', 'b'])
B['a'] + B['b']

sage: F.sum_of_monomials(['a', 'b', 'a'])
2*B['a'] + B['b']

F.sum_of_monomials is in fact (almost) a map:

sage: F.sum_of_monomials
A map to Free module generated by {'a', 'b', 'c'} over Rational Field

sum_of_terms(terms)

INPUT:

• terms: an list (or iterable) of pairs (index, coeff)

Returns the sum of the terms

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.sum_of_terms([('a',2), ('c',3)])
2*B['a'] + 3*B['c']

Extreme case:

sage: F.sum_of_terms([])
0

TODO: optimize, especially for the special case where all indices are distinct (should there be an option distinct=True for this, or a separate function sum_of_distinct_terms)?

term(index, coeff=None)

INPUT:

• index: the index of a basis element
• coeff: an element of the coefficient ring

Returns the corresponding term. The coefficient is assumed to be one if it is not given.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.term('a',3)
3*B['a']
sage: F.term('a')
B['a']

Design: should this do coercion on the coefficient ring?

zero(*args, **kwds)

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a', 'b', 'c'])
sage: F.zero()
0

class sage.combinat.free_module.CombinatorialFreeModuleElement(M, x)

Bases: sage.structure.element.Element

coefficient(m)

EXAMPLES:

sage: s = CombinatorialFreeModule(QQ, Partitions())
sage: z = s([4]) - 2*s([2,1]) + s([1,1,1]) + s([1])
sage: z.coefficient([4])
1
sage: z.coefficient([2,1])
-2
sage: z.coefficient(Partition([2,1]))
-2
sage: z.coefficient([1,2])
...
AssertionError: [1, 2] should be an element of Partitions
sage: z.coefficient(Composition([2,1]))
...
AssertionError: [2, 1] should be an element of Partitions

Test that coefficient also works for those parents that do not yet have an element_class:

sage: G = DihedralGroup(3)
sage: F = CombinatorialFreeModule(QQ, G)
sage: hasattr(G, "element_class")
False
sage: g = G.an_element()
sage: (2*F.monomial(g)).coefficient(g)
2

coefficients()

Returns a list of the coefficients appearing on the basiselements in self.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] - 3*B['c']
sage: f.coefficients()
[1, -3]

sage: s = SFASchur(QQ)
sage: z = s([4]) + s([2,1]) + s([1,1,1]) + s([1])
sage: z.coefficients()
[1, 1, 1, 1]

is_zero()

Returns True if and only self == 0.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] - 3*B['c']
sage: f.is_zero()
False
sage: F.zero().is_zero()
True

sage: s = SFASchur(QQ)
sage: s([2,1]).is_zero()
False
sage: s(0).is_zero()
True
sage: (s([2,1]) - s([2,1])).is_zero()
True

length()

Returns the number of basis elements of self with nonzero coefficients.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] - 3*B['c']
sage: f.length()
2

sage: s = SFASchur(QQ)
sage: z = s([4]) + s([2,1]) + s([1,1,1]) + s([1])
sage: z.length()
4

monomial_coefficients()

Return the internal dictionary which has the combinatorial objects indexing the basis as keys and their corresponding coefficients as values.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] + 3*B['c']
sage: d = f.monomial_coefficients()
sage: d['a']
1
sage: d['c']
3

sage: s = SFASchur(QQ)
sage: a = s([2,1])+2*s([3,2])
sage: d = a.monomial_coefficients()
sage: type(d)
<type 'dict'>
sage: d[ Partition([2,1]) ]
1
sage: d[ Partition([3,2]) ]
2

monomials()

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] + 2*B['c']
sage: f.monomials()
[B['a'], B['c']]

support()

Returns a list of the combinatorial objects indexing the basis elements of self which non-zero coefficients.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] - 3*B['c']
sage: f.support()
['a', 'c']

sage: s = SFASchur(QQ)
sage: z = s([4]) + s([2,1]) + s([1,1,1]) + s([1])
sage: z.support()
[[1], [1, 1, 1], [2, 1], [4]]

terms()

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] + 2*B['c']
sage: f.terms()
[B['a'], 2*B['c']]

to_vector()

Returns a vector version of self.

EXAMPLES:

sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] - 3*B['c']
sage: f.to_vector()
(1, 0, -3)

sage: QS3 = SymmetricGroupAlgebra(QQ, 3)
sage: a = 2*QS3([1,2,3])+4*QS3([3,2,1])
sage: a.to_vector()
(2, 0, 0, 0, 0, 4)
sage: a == QS3.from_vector(a.to_vector())
True

class sage.combinat.free_module.CombinatorialFreeModule_CartesianProduct(modules, **options)

Bases: sage.combinat.free_module.CombinatorialFreeModule

An implementation of cartesian products of modules with basis

EXAMPLES:

We construct two free modules, assign them short names, and construct their cartesian product:

sage: F = CombinatorialFreeModule(ZZ, [4,5]); F.__custom_name = "F"
sage: G = CombinatorialFreeModule(ZZ, [4,6]); G.__custom_name = "G"
sage: H = CombinatorialFreeModule(ZZ, [4,7]); H.__custom_name = "H"
sage: S = cartesian_product([F, G])
sage: S
F (+) G
sage: S.basis()
Lazy family (Term map from Disjoint union of Family ({4, 5}, {4, 6}) to F (+) G(i))_{i in Disjoint union of Family ({4, 5}, {4, 6})}

Note that the indices of the basis elements of F and G intersect non trivially. This is handled by forcing the union to be disjoint:

sage: list(S.basis())
[B[(0, 4)], B[(0, 5)], B[(1, 4)], B[(1, 6)]]

We now compute the cartesian product of elements of free modules:

sage: f =   F.monomial(4) + 2 * F.monomial(5)
sage: g = 2*G.monomial(4) +     G.monomial(6)
sage: h =   H.monomial(4) +     H.monomial(7)
sage: cartesian_product([f,g])
B[(0, 4)] + 2*B[(0, 5)] + 2*B[(1, 4)] + B[(1, 6)]
sage: cartesian_product([f,g,h])
B[(0, 4)] + 2*B[(0, 5)] + 2*B[(1, 4)] + B[(1, 6)] + B[(2, 4)] + B[(2, 7)]
sage: cartesian_product([f,g,h]).parent()
F (+) G (+) H

TODO: choose an appropriate semantic for cartesian products of cartesian products (associativity?):

sage: S = cartesian_product([cartesian_product([F, G]), H]) # todo: not implemented
F (+) G (+) H

class Element(M, x)

Bases: sage.combinat.free_module.CombinatorialFreeModuleElement

CombinatorialFreeModule_CartesianProduct.summand_embedding(*args, **kwds)

Returns the natural embedding morphism of the i-th summand of self into self

INPUTS:

• i – an integer

EXAMPLES:

sage: F = CombinatorialFreeModule(ZZ, [4,5]); F.__custom_name = "F"
sage: G = CombinatorialFreeModule(ZZ, [4,6]); G.__custom_name = "G"
sage: S = cartesian_product([F, G])
sage: phi = S.summand_embedding(0)
sage: phi(F.monomial(4) + 2 * F.monomial(5))
B[(0, 4)] + 2*B[(0, 5)]
sage: phi(F.monomial(4) + 2 * F.monomial(6)).parent() == S
True
sage: phi(G.monomial(4)) # not implemented Should raise an error!  problem: G(F.monomial(4)) does not complain!!!!

CombinatorialFreeModule_CartesianProduct.summand_projection(*args, **kwds)

Returns the natural projection onto the i-th summand of self

INPUTS:

• i – an integer

EXAMPLE:

sage: F = CombinatorialFreeModule(ZZ, [4,5]); F.__custom_name = "F"
sage: G = CombinatorialFreeModule(ZZ, [4,6]); G.__custom_name = "G"
sage: S = cartesian_product([F, G])
sage: x = S.monomial((0,4)) + 2 * S.monomial((0,5)) + 3 * S.monomial((1,6))
sage: S.summand_projection(0)(x)
B[4] + 2*B[5]
sage: S.summand_projection(1)(x)
3*B[6]
sage: S.summand_projection(0)(x).parent() == F
True
sage: S.summand_projection(1)(x).parent() == G
True

class sage.combinat.free_module.CombinatorialFreeModule_Tensor(modules, **options)

Bases: sage.combinat.free_module.CombinatorialFreeModule

Tensor Product of Free Modules

EXAMPLES:

We construct two free modules, assign them short names, and construct their tensor product:

sage: F = CombinatorialFreeModule(ZZ, [1,2]); F.__custom_name = "F"
sage: G = CombinatorialFreeModule(ZZ, [3,4]); G.__custom_name = "G"
sage: T = tensor([F, G]); T
F # G

sage: T.category()
Category of tensor products of modules with basis over Integer Ring

sage: T.construction() # todo: not implemented
[tensor, ]

T is a free module, with same base ring as F and G:

sage: T.base_ring()
Integer Ring

The basis of T is indexed by tuples of basis indices of F and G:

sage: T.basis().keys()
Image of Cartesian product of {1, 2}, {3, 4} by <type 'tuple'>
sage: T.basis().keys().list()
[(1, 3), (1, 4), (2, 3), (2, 4)]

FIXME: Should elements of a CartesianProduct be tuples (making them hashable)?

Here are the basis elements themselves:

sage: T.basis().cardinality()
4
sage: list(T.basis())
[B[1] # B[3], B[1] # B[4], B[2] # B[3], B[2] # B[4]]

The tensor product is associative and flattens sub tensor products:

sage: H = CombinatorialFreeModule(ZZ, [5,6]); H.rename("H")
sage: tensor([F, tensor([G, H])])
F # G # H
sage: tensor([tensor([F, G]), H])
F # G # H
sage: tensor([F, G, H])
F # G # H

We now compute the tensor product of elements of free modules:

sage: f =   F.monomial(1) + 2 * F.monomial(2)
sage: g = 2*G.monomial(3) +     G.monomial(4)
sage: h =   H.monomial(5) +     H.monomial(6)
sage: tensor([f, g])
2*B[1] # B[3] + B[1] # B[4] + 4*B[2] # B[3] + 2*B[2] # B[4]

Again, the tensor product is associative on elements:

sage: tensor([f, tensor([g, h])]) == tensor([f, g, h])
True
sage: tensor([tensor([f, g]), h]) == tensor([f, g, h])
True

Note further that the tensor product spaces need not preexist:

sage: t = tensor([f, g, h])
sage: t.parent()
F # G # H

TESTS:

sage: tensor([tensor([F, G]), H]) == tensor([F, G, H])
True
sage: tensor([F, tensor([G, H])]) == tensor([F, G, H])
True

tensor_constructor(*args, **kwds)

INPUT:

• modules – a tuple of free modules whose tensor product is self

Returns the canonical multilinear morphism from 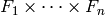to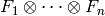

EXAMPLES:

sage: F = CombinatorialFreeModule(ZZ, [1,2]); F.__custom_name = "F"
sage: G = CombinatorialFreeModule(ZZ, [3,4]); G.__custom_name = "G"
sage: H = CombinatorialFreeModule(ZZ, [5,6]); H.rename("H")

sage: f =   F.monomial(1) + 2 * F.monomial(2)
sage: g = 2*G.monomial(3) +     G.monomial(4)
sage: h =   H.monomial(5) +     H.monomial(6)

sage: FG  = tensor([F, G   ])
sage: phi_fg = FG.tensor_constructor((F, G))
sage: phi_fg(f,g)
2*B[1] # B[3] + B[1] # B[4] + 4*B[2] # B[3] + 2*B[2] # B[4]

sage: FGH = tensor([F, G, H])
sage: phi_fgh = FGH.tensor_constructor((F, G, H))
sage: phi_fgh(f, g, h)
2*B[1] # B[3] # B[5] + 2*B[1] # B[3] # B[6] + B[1] # B[4] # B[5] + B[1] # B[4] # B[6] + 4*B[2] # B[3] # B[5] + 4*B[2] # B[3] # B[6] + 2*B[2] # B[4] # B[5] + 2*B[2] # B[4] # B[6]

sage: phi_fg_h = FGH.tensor_constructor((FG, H))
sage: phi_fg_h(phi_fg(f, g), h)
2*B[1] # B[3] # B[5] + 2*B[1] # B[3] # B[6] + B[1] # B[4] # B[5] + B[1] # B[4] # B[6] + 4*B[2] # B[3] # B[5] + 4*B[2] # B[3] # B[6] + 2*B[2] # B[4] # B[5] + 2*B[2] # B[4] # B[6]