Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »

AUTHORS:
Returns a Dyck word object or a head of a Dyck word object if the Dyck word is not complete.
EXAMPLES:
sage: dw = DyckWord([1, 0, 1, 0]); dw
[1, 0, 1, 0]
sage: print dw
()()
sage: print dw.height()
1
sage: dw.to_noncrossing_partition()
[[1], [2]]
sage: DyckWord('()()')
[1, 0, 1, 0]
sage: DyckWord('(())')
[1, 1, 0, 0]
sage: DyckWord('((')
[1, 1]
sage: DyckWord(noncrossing_partition=[[1],[2]])
[1, 0, 1, 0]
sage: DyckWord(noncrossing_partition=[[1,2]])
[1, 1, 0, 0]
TODO: In functions where a Dyck word is necessary, an error should be raised (e.g. a_statistic, b_statistic)?
Bases: sage.combinat.backtrack.GenericBacktracker
DyckWordBacktracker: this class is an iterator for all Dyck words with n opening parentheses and n - endht closing parentheses using the backtracker class. It is used by the DyckWords_size class.
This is not really meant to be called directly, partially because it fails in a couple corner cases: DWB(0) yields [0], not the empty word, and DWB(k, k+1) yields something (it shouldn’t yield anything). This could be fixed with a sanity check in _rec(), but then we’d be doing the sanity check every time we generate new objects; instead, we do one sanity check in DyckWords and assume here that the sanity check has already been made.
AUTHOR:
Bases: sage.combinat.combinat.CombinatorialObject
Returns the a-statistic for the Dyck word corresponding to the area of the Dyck path.
One can view a balanced Dyck word as a lattice path from
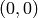 to
to 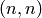 in the first quadrant by letting
‘1’s represent steps in the direction
in the first quadrant by letting
‘1’s represent steps in the direction 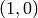 and ‘0’s
represent steps in the direction
and ‘0’s
represent steps in the direction 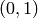 . The resulting
path will remain weakly above the diagonal
. The resulting
path will remain weakly above the diagonal 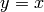 .
.
The a-statistic, or area statistic, is the number of complete
squares in the integer lattice which are below the path and above
the line 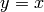 . The ‘half-squares’ directly above the
line
. The ‘half-squares’ directly above the
line 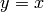 do not contribute to this statistic.
do not contribute to this statistic.
EXAMPLES:
sage: dw = DyckWord([1,0,1,0])
sage: dw.a_statistic() # 2 half-squares, 0 complete squares
0
sage: dw = DyckWord([1,1,1,0,1,1,1,0,0,0,1,1,0,0,1,0,0,0])
sage: dw.a_statistic()
19
sage: DyckWord([1,1,1,1,0,0,0,0]).a_statistic()
6
sage: DyckWord([1,1,1,0,1,0,0,0]).a_statistic()
5
sage: DyckWord([1,1,1,0,0,1,0,0]).a_statistic()
4
sage: DyckWord([1,1,1,0,0,0,1,0]).a_statistic()
3
sage: DyckWord([1,0,1,1,0,1,0,0]).a_statistic()
2
sage: DyckWord([1,1,0,1,1,0,0,0]).a_statistic()
4
sage: DyckWord([1,1,0,0,1,1,0,0]).a_statistic()
2
sage: DyckWord([1,0,1,1,1,0,0,0]).a_statistic()
3
sage: DyckWord([1,0,1,1,0,0,1,0]).a_statistic()
1
sage: DyckWord([1,0,1,0,1,1,0,0]).a_statistic()
1
sage: DyckWord([1,1,0,0,1,0,1,0]).a_statistic()
1
sage: DyckWord([1,1,0,1,0,0,1,0]).a_statistic()
2
sage: DyckWord([1,1,0,1,0,1,0,0]).a_statistic()
3
sage: DyckWord([1,0,1,0,1,0,1,0]).a_statistic()
0
Report the position for the parenthesis that matches the one at position pos.
INPUT:
OUTPUT:
Integer representing the index of the matching parenthesis. If no parenthesis matches, return None.
EXAMPLES:
sage: DyckWord([1, 0]).associated_parenthesis(0)
1
sage: DyckWord([1, 0, 1, 0]).associated_parenthesis(0)
1
sage: DyckWord([1, 0, 1, 0]).associated_parenthesis(1)
0
sage: DyckWord([1, 0, 1, 0]).associated_parenthesis(2)
3
sage: DyckWord([1, 0, 1, 0]).associated_parenthesis(3)
2
sage: DyckWord([1, 1, 0, 0]).associated_parenthesis(0)
3
sage: DyckWord([1, 1, 0, 0]).associated_parenthesis(2)
1
sage: DyckWord([1, 1, 0]).associated_parenthesis(1)
2
sage: DyckWord([1, 1]).associated_parenthesis(0)
Returns the b-statistic for the Dyck word corresponding to the bounce statistic of the Dyck word.
One can view a balanced Dyck word as a lattice path from 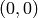 to
to
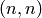 in the first quadrant by letting ‘1’s represent steps in
the direction
in the first quadrant by letting ‘1’s represent steps in
the direction 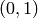 and ‘0’s represent steps in the direction
and ‘0’s represent steps in the direction
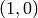 . The resulting path will remain weakly above the diagonal
. The resulting path will remain weakly above the diagonal
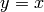 .
.
We describe the b-statistic of such a path in terms of what is known as the “bounce path”.
We can think of our bounce path as describing the trail of a billiard ball shot West from (n, n), which “bounces” down whenever it encounters a vertical step and “bounces” left when it encounters the line y = x.
The bouncing ball will strike the diagonal at places
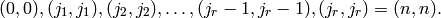
We define the b-statistic to be the sum 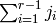 .
.
EXAMPLES:
sage: dw = DyckWord([1,1,1,0,1,1,1,0,0,0,1,1,0,0,1,0,0,0])
sage: dw.b_statistic()
7
sage: DyckWord([1,1,1,1,0,0,0,0]).b_statistic()
0
sage: DyckWord([1,1,1,0,1,0,0,0]).b_statistic()
1
sage: DyckWord([1,1,1,0,0,1,0,0]).b_statistic()
2
sage: DyckWord([1,1,1,0,0,0,1,0]).b_statistic()
3
sage: DyckWord([1,0,1,1,0,1,0,0]).b_statistic()
3
sage: DyckWord([1,1,0,1,1,0,0,0]).b_statistic()
1
sage: DyckWord([1,1,0,0,1,1,0,0]).b_statistic()
2
sage: DyckWord([1,0,1,1,1,0,0,0]).b_statistic()
1
sage: DyckWord([1,0,1,1,0,0,1,0]).b_statistic()
4
sage: DyckWord([1,0,1,0,1,1,0,0]).b_statistic()
3
sage: DyckWord([1,1,0,0,1,0,1,0]).b_statistic()
5
sage: DyckWord([1,1,0,1,0,0,1,0]).b_statistic()
4
sage: DyckWord([1,1,0,1,0,1,0,0]).b_statistic()
2
sage: DyckWord([1,0,1,0,1,0,1,0]).b_statistic()
6
REFERENCES:
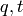 -Catalan Numbers and the Space of
Diagonal Harmonics: With an Appendix on the Combinatorics of
Macdonald Polynomials - James Haglund, University of
Pennsylvania, Philadelphia - AMS, 2008, 167 pp.
-Catalan Numbers and the Space of
Diagonal Harmonics: With an Appendix on the Combinatorics of
Macdonald Polynomials - James Haglund, University of
Pennsylvania, Philadelphia - AMS, 2008, 167 pp.Bijection from non-decreasing parking functions. See there the method to_dyck_word() for more information.
EXAMPLES:
sage: from sage.combinat.dyck_word import DyckWord_class
sage: DyckWord_class.from_non_decreasing_parking_function([])
[]
sage: DyckWord_class.from_non_decreasing_parking_function([1])
[1, 0]
sage: DyckWord_class.from_non_decreasing_parking_function([1,1])
[1, 1, 0, 0]
sage: DyckWord_class.from_non_decreasing_parking_function([1,2])
[1, 0, 1, 0]
sage: DyckWord_class.from_non_decreasing_parking_function([1,1,1])
[1, 1, 1, 0, 0, 0]
sage: DyckWord_class.from_non_decreasing_parking_function([1,2,3])
[1, 0, 1, 0, 1, 0]
sage: DyckWord_class.from_non_decreasing_parking_function([1,1,3,3,4,6,6])
[1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0]
TESTS:
sage: DyckWord_class.from_non_decreasing_parking_function(NonDecreasingParkingFunction([]))
[]
sage: DyckWord_class.from_non_decreasing_parking_function(NonDecreasingParkingFunction([1,1,3,3,4,6,6]))
[1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0]
Returns the height of the Dyck word.
We view the Dyck word as a Dyck path from 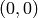 to
to
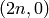 in the first quadrant by letting ‘1’s represent
steps in the direction
in the first quadrant by letting ‘1’s represent
steps in the direction 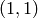 and ‘0’s represent steps in
the direction
and ‘0’s represent steps in
the direction 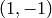 .
.
The height is the maximum  -coordinate reached.
-coordinate reached.
EXAMPLES:
sage: DyckWord([]).height()
0
sage: DyckWord([1,0]).height()
1
sage: DyckWord([1, 1, 0, 0]).height()
2
sage: DyckWord([1, 1, 0, 1, 0]).height()
2
sage: DyckWord([1, 1, 0, 0, 1, 0]).height()
2
sage: DyckWord([1, 0, 1, 0]).height()
1
sage: DyckWord([1, 1, 0, 0, 1, 1, 1, 0, 0, 0]).height()
3
Returns a list of the positions of the peaks of a Dyck word. A peak
is 1 followed by a 0. Note that this does not agree with the
definition given by Haglund in: The 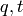 -Catalan Numbers
and the Space of Diagonal Harmonics: With an Appendix on the
Combinatorics of Macdonald Polynomials - James Haglund, University
of Pennsylvania, Philadelphia - AMS, 2008, 167 pp.
-Catalan Numbers
and the Space of Diagonal Harmonics: With an Appendix on the
Combinatorics of Macdonald Polynomials - James Haglund, University
of Pennsylvania, Philadelphia - AMS, 2008, 167 pp.
EXAMPLES:
sage: DyckWord([1, 0, 1, 0]).peaks()
[0, 2]
sage: DyckWord([1, 1, 0, 0]).peaks()
[1]
sage: DyckWord([1,1,0,1,0,1,0,0]).peaks() # Haglund's def gives 2
[1, 3, 5]
Returns the size which is the number of opening parentheses.
EXAMPLES:
sage: DyckWord([1, 0, 1, 0]).size()
2
sage: DyckWord([1, 0, 1, 1, 0]).size()
3
Bijection to non-decreasing parking functions. See there the method to_dyck_word() for more information.
EXAMPLES:
sage: DyckWord([]).to_non_decreasing_parking_function()
[]
sage: DyckWord([1,0]).to_non_decreasing_parking_function()
[1]
sage: DyckWord([1,1,0,0]).to_non_decreasing_parking_function()
[1, 1]
sage: DyckWord([1,0,1,0]).to_non_decreasing_parking_function()
[1, 2]
sage: DyckWord([1,0,1,1,0,1,0,0,1,0]).to_non_decreasing_parking_function()
[1, 2, 2, 3, 5]
TESTS:
sage: ld=DyckWords(5);
sage: list(ld) == [dw.to_non_decreasing_parking_function().to_dyck_word() for dw in ld]
True
Bijection of Biane from Dyck words to non-crossing partitions. Thanks to Mathieu Dutour for describing the bijection.
EXAMPLES:
sage: DyckWord([]).to_noncrossing_partition()
[]
sage: DyckWord([1, 0]).to_noncrossing_partition()
[[1]]
sage: DyckWord([1, 1, 0, 0]).to_noncrossing_partition()
[[1, 2]]
sage: DyckWord([1, 1, 1, 0, 0, 0]).to_noncrossing_partition()
[[1, 2, 3]]
sage: DyckWord([1, 0, 1, 0, 1, 0]).to_noncrossing_partition()
[[1], [2], [3]]
sage: DyckWord([1, 1, 0, 1, 0, 0]).to_noncrossing_partition()
[[2], [1, 3]]
TESTS:
sage: DyckWord([1, 1, 0, 0]).to_ordered_tree()
...
NotImplementedError: TODO
Returns a standard tableau of length less than or equal to 2 with the size the same as the length of the list. The standard tableau will be rectangular iff self is a complete Dyck word.
EXAMPLES:
sage: DyckWord([]).to_tableau()
[]
sage: DyckWord([1, 0]).to_tableau()
[[2], [1]]
sage: DyckWord([1, 1, 0, 0]).to_tableau()
[[3, 4], [1, 2]]
sage: DyckWord([1, 0, 1, 0]).to_tableau()
[[2, 4], [1, 3]]
sage: DyckWord([1]).to_tableau()
[[1]]
sage: DyckWord([1, 0, 1]).to_tableau()
[[2], [1, 3]]
TODO: better name? to_standard_tableau? and should actually return a Tableau object?
TESTS:
sage: DyckWord([1, 1, 0, 0]).to_triangulation()
...
NotImplementedError: TODO
Returns the combinatorial class of Dyck words. A Dyck word is a
sequence 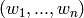 consisting of ‘1’s and ‘0’s,
with the property that for any
consisting of ‘1’s and ‘0’s,
with the property that for any  with
with
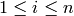 , the sequence
, the sequence 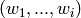 contains at least as many
contains at least as many  s as
s as  .
.
A Dyck word is balanced if the total number of ‘1’s is equal to the
total number of ‘0’s. The number of balanced Dyck words of length
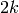 is given by the Catalan number
is given by the Catalan number 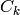 .
.
EXAMPLES: If neither k1 nor k2 are specified, then DyckWords returns the combinatorial class of all balanced Dyck words.
sage: DW = DyckWords(); DW
Dyck words
sage: [] in DW
True
sage: [1, 0, 1, 0] in DW
True
sage: [1, 1, 0] in DW
False
If just k1 is specified, then it returns the combinatorial class of balanced Dyck words with k1 opening parentheses and k1 closing parentheses.
sage: DW2 = DyckWords(2); DW2
Dyck words with 2 opening parentheses and 2 closing parentheses
sage: DW2.first()
[1, 0, 1, 0]
sage: DW2.last()
[1, 1, 0, 0]
sage: DW2.cardinality()
2
sage: DyckWords(100).cardinality() == catalan_number(100)
True
If k2 is specified in addition to k1, then it returns the combinatorial class of Dyck words with k1 opening parentheses and k2 closing parentheses.
sage: DW32 = DyckWords(3,2); DW32
Dyck words with 3 opening parentheses and 2 closing parentheses
sage: DW32.list()
[[1, 0, 1, 0, 1],
[1, 0, 1, 1, 0],
[1, 1, 0, 0, 1],
[1, 1, 0, 1, 0],
[1, 1, 1, 0, 0]]
Bases: sage.combinat.combinat.CombinatorialClass
Returns the number of Dyck words of size n, i.e. the n-th Catalan number.
EXAMPLES:
sage: DyckWords(4).cardinality()
14
sage: ns = range(9)
sage: dws = [DyckWords(n) for n in ns]
sage: all([ dw.cardinality() == len(dw.list()) for dw in dws])
True
Returns a list of all the Dyck words with k1 opening and k2 closing parentheses.
EXAMPLES:
sage: DyckWords(0).list()
[[]]
sage: DyckWords(1).list()
[[1, 0]]
sage: DyckWords(2).list()
[[1, 0, 1, 0], [1, 1, 0, 0]]
Converts a non-crossing partition to a Dyck word.
TESTS:
sage: DyckWord(noncrossing_partition=[[1,2]]) # indirect doctest
[1, 1, 0, 0]
sage: DyckWord(noncrossing_partition=[[1],[2]])
[1, 0, 1, 0]
sage: dws = DyckWords(5).list()
sage: ncps = map( lambda x: x.to_noncrossing_partition(), dws)
sage: dws2 = map( lambda x: DyckWord(noncrossing_partition=x), ncps)
sage: dws == dws2
True
TESTS:
sage: sage.combinat.dyck_word.from_ordered_tree(1)
...
NotImplementedError: TODO
If k1 is specified, then the object must have exactly k1 open symbols. If k2 is also specified, then obj must have exactly k2 close symbols.
EXAMPLES:
sage: from sage.combinat.dyck_word import is_a
sage: is_a([1,1,0,0])
True
sage: is_a([1,0,1,0])
True
sage: is_a([1,1,0,0],2)
True
sage: is_a([1,1,0,0],3)
False
If k1 is specified, then the object must have exactly k1 open symbols. If k2 is also specified, then obj must have exactly k2 close symbols.
EXAMPLES:
sage: from sage.combinat.dyck_word import is_a_prefix
sage: is_a_prefix([1,1,0])
True
sage: is_a_prefix([0,1,0])
False
sage: is_a_prefix([1,1,0],2,1)
True
sage: is_a_prefix([1,1,0],1,1)
False
A map from '(' to open_symbol and ')' to close_symbol and otherwise an error is raised. The values of the constants open_symbol and close_symbol are subject to change. This is the inverse map of replace_symbols().
INPUT:
OUTPUT:
See also
EXAMPLES:
sage: from sage.combinat.dyck_word import replace_parens
sage: replace_parens('(')
1
sage: replace_parens(')')
0
sage: replace_parens(1)
...
ValueError
A map from open_symbol to '(' and close_symbol to ')' and otherwise an error is raised. The values of the constants open_symbol and close_symbol are subject to change. This is the inverse map of replace_parens().
INPUT:
OUTPUT:
See also
EXAMPLES:
sage: from sage.combinat.dyck_word import replace_symbols
sage: replace_symbols(1)
'('
sage: replace_symbols(0)
')'
sage: replace_symbols(3)
...
ValueError