Integer compositions

A composition of a nonnegative integer is a list of positive integers (the parts of the compositions) with total sum .

This module provides tools for manipulating compositions and enumerated sets of compositions.

EXAMPLES:

sage: Composition([5, 3, 1, 3])
[5, 3, 1, 3]
sage: list(Compositions(4))
[[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 3], [2, 1, 1], [2, 2], [3, 1], [4]]

AUTHORS:

• Mike Hansen, Nicolas M. Thiery
• MuPAD-Combinat developers (algorithms and design inspiration)

sage.combinat.composition.Composition(co=None, descents=None, code=None)

Integer compositions

A composition of a nonnegative integer is a list of positive integers with total sum .

TODO: mathematical definition of descents, code, ...

EXAMPLES:

The simplest way to create a composition is by specifying its entries as a list, tuple (or other iterable):

sage: Composition([3,1,2])
[3, 1, 2]
sage: Composition((3,1,2))
[3, 1, 2]
sage: Composition(i for i in range(2,5))
[2, 3, 4]

You can alternatively create a composition from the list of its descents:

sage: Composition([1, 1, 3, 4, 3]).descents()
[0, 1, 4, 8, 11]
sage: Composition(descents=[1,0,4,8,11])
[1, 1, 3, 4, 3]

You can also create a composition from its code:

sage: Composition([4,1,2,3,5]).to_code()
[1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]
sage: Composition(code=_)
[4, 1, 2, 3, 5]
sage: Composition([3,1,2,3,5]).to_code()
[1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]
sage: Composition(code=_)
[3, 1, 2, 3, 5]

class sage.combinat.composition.Composition_class(l)

Bases: sage.combinat.combinat.CombinatorialObject

Integer compositions

A composition of a nonnegative integer is a list of positive integers with total sum .

TODO: mathematical definition of descents, code, ...

EXAMPLES:

The simplest way to create a composition is by specifying its entries as a list, tuple (or other iterable):

sage: Composition([3,1,2])
[3, 1, 2]
sage: Composition((3,1,2))
[3, 1, 2]
sage: Composition(i for i in range(2,5))
[2, 3, 4]

You can alternatively create a composition from the list of its descents:

sage: Composition([1, 1, 3, 4, 3]).descents()
[0, 1, 4, 8, 11]
sage: Composition(descents=[1,0,4,8,11])
[1, 1, 3, 4, 3]

You can also create a composition from its code:

sage: Composition([4,1,2,3,5]).to_code()
[1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]
sage: Composition(code=_)
[4, 1, 2, 3, 5]
sage: Composition([3,1,2,3,5]).to_code()
[1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]
sage: Composition(code=_)
[3, 1, 2, 3, 5]

complement()

Returns the complement of the composition co. The complement is the reverse of co’s conjugate composition.

EXAMPLES:

sage: Composition([1, 1, 3, 1, 2, 1, 3]).conjugate()
[1, 1, 3, 3, 1, 3]
sage: Composition([1, 1, 3, 1, 2, 1, 3]).complement()
[3, 1, 3, 3, 1, 1]

conjugate()

Returns the conjugate of the composition comp.

Algorithm from mupad-combinat.

EXAMPLES:

sage: Composition([1, 1, 3, 1, 2, 1, 3]).conjugate()  
[1, 1, 3, 3, 1, 3]

descents(final_descent=False)

Returns the list of descents of the composition co.

EXAMPLES:

sage: Composition([1, 1, 3, 1, 2, 1, 3]).descents()
[0, 1, 4, 5, 7, 8, 11]

fatten(grouping)

Returns the composition fatter than self, obtained by grouping together consecutive parts according to grouping.

INPUT:

• grouping – a composition whose sum is the length of self

EXAMPLES:

Let us start with the composition:

sage: c = Composition([4,5,2,7,1])

With 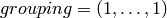, is left unchanged:

sage: c.fatten(Composition([1,1,1,1,1]))
[4, 5, 2, 7, 1]

With 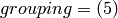, this yields the coarser composition above :

sage: c.fatten(Composition([5]))
[19]

Other values for grouping yield (all the) other compositions coarser to :

sage: c.fatten(Composition([2,1,2]))
[9, 2, 8]
sage: c.fatten(Composition([3,1,1]))
[11, 7, 1]

TESTS:

sage: Composition([]).fatten(Composition([]))
[]
sage: c.fatten(Composition([3,1,1])).__class__ == c.__class__
True

fatter()

Returns the set of compositions which are fatter than self.

Complexity for generation: O(size(c)) memory, O(size(result)) time

EXAMPLES:

sage: C = Composition([4,5,2]).fatter()
sage: C.cardinality()
4
sage: list(C)
[[4, 5, 2], [4, 7], [9, 2], [11]]

Some extreme cases:

sage: list(Composition([5]).fatter())
[[5]]
sage: list(Composition([]).fatter())
[[]]
sage: list(Composition([1,1,1,1]).fatter()) == list(Compositions(4))
True

finer()

Returns the set of compositions which are finer than self.

EXAMPLES:

sage: C = Composition([3,2]).finer()
sage: C.cardinality()
8
sage: list(C)
[[1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 2, 1, 1], [1, 2, 2], [2, 1, 1, 1], [2, 1, 2], [3, 1, 1], [3, 2]]

is_finer(co2)

Returns True if the composition self is finer than the composition co2; otherwise, it returns False.

EXAMPLES:

sage: Composition([4,1,2]).is_finer([3,1,3])
False
sage: Composition([3,1,3]).is_finer([4,1,2])
False
sage: Composition([1,2,2,1,1,2]).is_finer([5,1,3])
True
sage: Composition([2,2,2]).is_finer([4,2])
True

major_index()

Returns the major index of the composition co. The major index is defined as the sum of the descents.

EXAMPLES:

sage: Composition([1, 1, 3, 1, 2, 1, 3]).major_index()
31

peaks()

Returns a list of the peaks of the composition self. The peaks of a composition are the descents which do not immediately follow another descent.

EXAMPLES:

sage: Composition([1, 1, 3, 1, 2, 1, 3]).peaks()
[4, 7]

refinement(co2)

Returns the refinement composition of self and co2.

EXAMPLES:

sage: Composition([1,2,2,1,1,2]).refinement([5,1,3])
[3, 1, 2]

size()

Returns the size of the composition, that is the sum of its parts.

EXAMPLES:

sage: Composition([7,1,3]).size()
11

static sum(compositions)

Returns the concatenation of the given compositions.

INPUT:

• compositions – a list (or iterable) of compositions

EXAMPLES:

sage: sage.combinat.composition.Composition_class.sum([Composition([1, 1, 3]), Composition([4, 1, 2]), Composition([3,1])])
[1, 1, 3, 4, 1, 2, 3, 1]

Any iterable can be provided as input:

sage: sage.combinat.composition.Composition_class.sum([Composition([i,i]) for i in [4,1,3]])
[4, 4, 1, 1, 3, 3]

Empty inputs are handled gracefully:

sage: sage.combinat.composition.Composition_class.sum([]) == Composition([])
True

to_code()

Returns the code of the composition self. The code of a composition is a list of length self.size() of 1s and 0s such that there is a 1 wherever a new part starts.

EXAMPLES:

sage: Composition([4,1,2,3,5]).to_code()
[1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]

to_skew_partition(overlap=1)

Returns the skew partition obtained from the composition co. The parameter overlap indicates the number of cells that are covered by cells of the previous line.

EXAMPLES:

sage: Composition([3,4,1]).to_skew_partition()
[[6, 6, 3], [5, 2]]
sage: Composition([3,4,1]).to_skew_partition(overlap=0)
[[8, 7, 3], [7, 3]]

sage.combinat.composition.Compositions(n=None, **kwargs)

Sets of integer Compositions.

A composition of a nonnegative integer is a list of positive integers with total sum .

See also: Composition, Partitions, IntegerVectors

EXAMPLES:

There are 8 compositions of 4:

sage: Compositions(4).cardinality()
8

Here is the list of them:

sage: list(Compositions(4))
[[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 3], [2, 1, 1], [2, 2], [3, 1], [4]]

You can use the .first() method to get the ‘first’ composition of a number:

sage: Compositions(4).first()
[1, 1, 1, 1]

You can also calculate the ‘next’ composition given the current one:

sage: Compositions(4).next([1,1,2])
[1, 2, 1]

If is not specified, this returns the combinatorial class of all (non-negative) integer compositions:

sage: Compositions()
Compositions of non-negative integers
sage: [] in Compositions()
True
sage: [2,3,1] in Compositions()
True
sage: [-2,3,1] in Compositions()
False

If n is specified, it returns the class of compositions of n:

sage: Compositions(3)
Compositions of 3
sage: list(Compositions(3))
[[1, 1, 1], [1, 2], [2, 1], [3]]
sage: Compositions(3).cardinality()
4

The following examples show how to test whether or not an object is a composition:

sage: [3,4] in Compositions()
True
sage: [3,4] in Compositions(7)
True
sage: [3,4] in Compositions(5)
False

Similarly, one can check whether or not an object is a composition which satisfies further constraints:

sage: [4,2] in Compositions(6, inner=[2,2])
True
sage: [4,2] in Compositions(6, inner=[2,3])
False
sage: [4,1] in Compositions(5, inner=[2,1], max_slope = 0)
True

Note that the given constraints should be compatible:

sage: [4,2] in Compositions(6, inner=[2,2], min_part=3) # 
True

The options length, min_length, and max_length can be used to set length constraints on the compositions. For example, the compositions of 4 of length equal to, at least, and at most 2 are given by:

sage: Compositions(4, length=2).list()
[[3, 1], [2, 2], [1, 3]]
sage: Compositions(4, min_length=2).list()
[[3, 1], [2, 2], [2, 1, 1], [1, 3], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
sage: Compositions(4, max_length=2).list()
[[4], [3, 1], [2, 2], [1, 3]]

Setting both min_length and max_length to the same value is equivalent to setting length to this value:

sage: Compositions(4, min_length=2, max_length=2).list()
[[3, 1], [2, 2], [1, 3]]

The options inner and outer can be used to set part-by-part containment constraints. The list of compositions of 4 bounded above by [3,1,2] is given by:

sage: list(Compositions(4, outer=[3,1,2]))
[[3, 1], [2, 1, 1], [1, 1, 2]]

Outer sets max_length to the length of its argument. Moreover, the parts of outer may be infinite to clear the constraint on specific parts. This is the list of compositions of 4 of length at most 3 such that the first and third parts are at most 1:

sage: list(Compositions(4, outer=[1,oo,1]))
[[1, 3], [1, 2, 1]]

This is the list of compositions of 4 bounded below by [1,1,1]:

sage: list(Compositions(4, inner=[1,1,1]))
[[2, 1, 1], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]

The options min_slope and max_slope can be used to set constraints on the slope, that is the difference of two consecutive parts. The following is the list of weakly increasing compositions of 4:

sage: Compositions(4, min_slope=0).list()
[[4], [2, 2], [1, 3], [1, 1, 2], [1, 1, 1, 1]]

Here are the weakly decreasing ones:

sage: Compositions(4, max_slope=0).list()
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]

The following is the list of compositions of 4 such that two consecutive parts differ by at most one:

sage: Compositions(4, min_slope=-1, max_slope=1).list()
[[4], [2, 2], [2, 1, 1], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]

The constraints can be combined together in all reasonable ways. This is the list of compositions of 5 of length between 2 and 4 such that the difference between consecutive parts is between -2 and 1:

sage: Compositions(5, max_slope=1, min_slope=-2, min_length=2, max_length=4).list()
[[3, 2], [3, 1, 1], [2, 3], [2, 2, 1], [2, 1, 2], [2, 1, 1, 1], [1, 2, 2], [1, 2, 1, 1], [1, 1, 2, 1], [1, 1, 1, 2]]

We can do the same thing with an outer constraint:

sage: Compositions(5, max_slope=1, min_slope=-2, min_length=2, max_length=4, outer=[2,5,2]).list()
[[2, 3], [2, 2, 1], [2, 1, 2], [1, 2, 2]]

However, providing incoherent constraints may yield strange results. It is up to the user to ensure that the inner and outer compositions themselves satisfy the parts and slope constraints.

Note that if you specify min_part=0, then the objects produced may have parts equal to zero. This violates the internal assumptions that the Composition class makes. Use at your own risk, or preferably consider using IntegerVectors instead:

sage: list(Compositions(2, length=3, min_part=0))
doctest:... RuntimeWarning: Currently, setting min_part=0 produces Composition objects which violate internal assumptions.  Calling methods on these objects may produce errors or WRONG results!
[[2, 0, 0], [1, 1, 0], [1, 0, 1], [0, 2, 0], [0, 1, 1], [0, 0, 2]]

sage: list(IntegerVectors(2, 3))
[[2, 0, 0], [1, 1, 0], [1, 0, 1], [0, 2, 0], [0, 1, 1], [0, 0, 2]]

The generation algorithm is constant amortized time, and handled by the generic tool IntegerListsLex.

TESTS:

sage: C = Compositions(4, length=2)
sage: C == loads(dumps(C))
True

sage: Compositions(6, min_part=2, length=3)
Compositions of the integer 6 satisfying constraints length=3, min_part=2


sage: [2, 1] in Compositions(3, length=2)
True
sage: [2,1,2] in Compositions(5, min_part=1)
True
sage: [2,1,2] in Compositions(5, min_part=2)
False

sage: Compositions(4, length=2).cardinality()
3
sage: Compositions(4, min_length=2).cardinality()
7
sage: Compositions(4, max_length=2).cardinality()
4
sage: Compositions(4, max_part=2).cardinality()
5
sage: Compositions(4, min_part=2).cardinality()
2
sage: Compositions(4, outer=[3,1,2]).cardinality()
3

sage: Compositions(4, length=2).list()
[[3, 1], [2, 2], [1, 3]]
sage: Compositions(4, min_length=2).list()
[[3, 1], [2, 2], [2, 1, 1], [1, 3], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
sage: Compositions(4, max_length=2).list()
[[4], [3, 1], [2, 2], [1, 3]]
sage: Compositions(4, max_part=2).list()
[[2, 2], [2, 1, 1], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
sage: Compositions(4, min_part=2).list()
[[4], [2, 2]]
sage: Compositions(4, outer=[3,1,2]).list()
[[3, 1], [2, 1, 1], [1, 1, 2]]
sage: Compositions(4, outer=[1,oo,1]).list()
[[1, 3], [1, 2, 1]]
sage: Compositions(4, inner=[1,1,1]).list()
[[2, 1, 1], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
sage: Compositions(4, min_slope=0).list()
[[4], [2, 2], [1, 3], [1, 1, 2], [1, 1, 1, 1]]
sage: Compositions(4, min_slope=-1, max_slope=1).list()
[[4], [2, 2], [2, 1, 1], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
sage: Compositions(5, max_slope=1, min_slope=-2, min_length=2, max_length=4).list()
[[3, 2], [3, 1, 1], [2, 3], [2, 2, 1], [2, 1, 2], [2, 1, 1, 1], [1, 2, 2], [1, 2, 1, 1], [1, 1, 2, 1], [1, 1, 1, 2]]
sage: Compositions(5, max_slope=1, min_slope=-2, min_length=2, max_length=4, outer=[2,5,2]).list()
[[2, 3], [2, 2, 1], [2, 1, 2], [1, 2, 2]]

class sage.combinat.composition.Compositions_all

Bases: sage.combinat.combinat.InfiniteAbstractCombinatorialClass

Element

alias of Composition_class

class sage.combinat.composition.Compositions_constraints(n, length=None, min_length=0, max_length=+Infinity, floor=None, ceiling=None, min_part=0, max_part=+Infinity, min_slope=-Infinity, max_slope=+Infinity, name=None, element_constructor=None)

Bases: sage.combinat.integer_list.IntegerListsLex

class sage.combinat.composition.Compositions_n(n)

Bases: sage.combinat.combinat.CombinatorialClass

cardinality()

TESTS:

sage: Compositions(3).cardinality()
4
sage: Compositions(0).cardinality()
1

list()

TESTS:

sage: Compositions(4).list()
[[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 3], [2, 1, 1], [2, 2], [3, 1], [4]]
sage: Compositions(0).list()
[[]]

sage.combinat.composition.from_code(code)

Return the composition from its code.The code of a composition is a list of length self.size() of 1s and 0s such that there is a 1 wherever a new part starts.

EXAMPLES:

sage: import sage.combinat.composition as composition
sage: Composition([4,1,2,3,5]).to_code()
[1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]
sage: composition.from_code(_)          
[4, 1, 2, 3, 5]
sage: Composition([3,1,2,3,5]).to_code()
[1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]
sage: composition.from_code(_)          
[3, 1, 2, 3, 5]

sage.combinat.composition.from_descents(descents, nps=None)

Returns a composition from the list of descents.

EXAMPLES:

sage: Composition([1, 1, 3, 4, 3]).descents()
[0, 1, 4, 8, 11]
sage: sage.combinat.composition.from_descents([1,0,4,8],12)
[1, 1, 3, 4, 3]
sage: sage.combinat.composition.from_descents([1,0,4,8,11])
[1, 1, 3, 4, 3]