Binary self-dual codes

This module implements functions useful for studying binary self-dual codes. The main function is self_dual_codes_binary, which is a case-by-case list of entries, each represented by a Python dictionary.

Format of each entry: a Python dictionary with keys “order autgp”, “spectrum”, “code”, “Comment”, “Type”, where

• “code” - a sd code C of length n, dim n/2, over GF(2)
• “order autgp” - order of the permutation automorphism group of C
• “Type” - the type of C (which can be “I” or “II”, in the binary case)
• “spectrum” - the spectrum [A0,A1,...,An]
• “Comment” - possibly an empty string.

Python dictionaries were used since they seemed to be both human-readable and allow others to update the database easiest.

• The following double for loop can be time-consuming but should be run once in awhile for testing purposes. It should only print True and have no trace-back errors:

  for n in [4,6,8,10,12,14,16,18,20,22]:
       C = self_dual_codes_binary(n); m = len(C.keys())
       for i in range(m):
           C0 = C["%s"%n]["%s"%i]["code"]
           print n, '  ',i, '    ',C["%s"%n]["%s"%i]["spectrum"] == C0.spectrum()
           print C0 == C0.dual_code()
           G = C0.automorphism_group_binary_code()
           print C["%s"%n]["%s"%i]["order autgp"] == G.order()
  

• To check if the “Riemann hypothesis” holds, run the following code:

  R = PolynomialRing(CC,"T")      
  T = R.gen()
  for n in [4,6,8,10,12,14,16,18,20,22]:
       C = self_dual_codes_binary(n); m = len(C["%s"%n].keys())
       for i in range(m):
           C0 = C["%s"%n]["%s"%i]["code"]
           if C0.minimum_distance()>2:
               f = R(C0.sd_zeta_polynomial())
               print n,i,[z[0].abs() for z in f.roots()]
  

You should get lists of numbers equal to 0.707106781186548.

Here’s a rather naive construction of self-dual codes in the binary case:

For even m, let A_m denote the mxm matrix over GF(2) given by adding the all 1’s matrix to the identity matrix (in MatrixSpace(GF(2),m,m) of course). If M_1, ..., M_r are square matrices, let 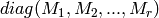denote the”block diagonal” matrix with the 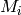‘s on the diagonal and 0’s elsewhere. Let 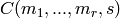denote the linear code with generator matrix having block form 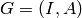, where 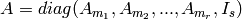, for some (even) 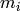‘s and , where 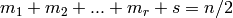. Note: Such codes 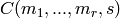are SD.

SD codes not of this form will be called (for the purpose of documenting the code below) “exceptional”. Except when n is “small”, most sd codes are exceptional (based on a counting argument and table 9.1 in the Huffman+Pless [HP], page 347).

---

AUTHORS:

• David Joyner (2007-08-11)

REFERENCES:

• [HP] W. C. Huffman, V. Pless, Fundamentals of Error-Correcting Codes, Cambridge Univ. Press, 2003.
• [P] V. Pless, “A classification of self-orthogonal codes over GF(2)”, Discrete Math 3 (1972) 209-246.

sage.coding.sd_codes.I2(n)

sage.coding.sd_codes.MS(n)

sage.coding.sd_codes.MS2(n)

sage.coding.sd_codes.matA(n)

sage.coding.sd_codes.matId(n)

sage.coding.sd_codes.self_dual_codes_binary(n)

Returns the dictionary of inequivalent sd codes of length n.

For n=4 even, returns the sd codes of a given length, up to (perm) equivalence, the (perm) aut gp, and the type.

The number of inequiv “diagonal” sd binary codes in the database of length n is (“diagonal” is defined by the conjecture above) is the same as the restricted partition number of n, where only integers from the set 1,4,6,8,... are allowed. This is the coefficient of 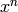in the series expansion 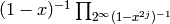. Typing the command f = (1-x)(-1)*prod([(1-x(2*j))(-1) for j in range(2,18)]) into Sage, we obtain for the coeffs of , , ... 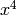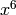[1, 1, 2, 2, 3, 3, 5, 5, 7, 7, 11, 11, 15, 15, 22, 22, 30, 30, 42, 42, 56, 56, 77, 77, 101, 101, 135, 135, 176, 176, 231] These numbers grow too slowly to account for all the sd codes (see Huffman+Pless’ Table 9.1, referenced above). In fact, in Table 9.10 of [HP], the number B_n of inequivalent sd binary codes of length n is given:

n   2 4 6 8 10 12 14 16 18 20 22 24  26  28  30 
B_n 1 1 1 2  2  3  4  7  9 16 25 55 103 261 731

According to http://www.research.att.com/~njas/sequences/A003179, the next 2 entries are: 3295, 24147.

EXAMPLES:

sage: C = self_dual_codes_binary(10)
sage: C["10"]["0"]["code"] == C["10"]["0"]["code"].dual_code()
True
sage: C["10"]["1"]["code"] == C["10"]["1"]["code"].dual_code()
True
sage: len(C["10"].keys()) # number of inequiv sd codes of length 10
2
sage: C = self_dual_codes_binary(12) 
sage: C["12"]["0"]["code"] == C["12"]["0"]["code"].dual_code()
True
sage: C["12"]["1"]["code"] == C["12"]["1"]["code"].dual_code()
True
sage: C["12"]["2"]["code"] == C["12"]["2"]["code"].dual_code()
True