Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Coding Theory »

AUTHOR:
This file contains constructions of error-correcting codes which are pure Python/Sage and not obtained from wrapping GUAVA functions. The GUAVA wrappers are in guava.py.
Let  be a finite field with
be a finite field with  elements.
Here’s a constructive definition of a cyclic code of length
elements.
Here’s a constructive definition of a cyclic code of length
 .
.
![g(x)\in F[x]](../../_images/math/78453a1459e69a70754b04ef9d17a20b2bede9c1.png) dividing
dividing
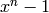 . This is called the generating polynomial of the
code.
. This is called the generating polynomial of the
code.![p(x)\in F[x]](../../_images/math/f72923dac4b6744cb062a2897cb41a6919f5c344.png) , compute
, compute
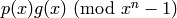 . Denote the answer by
. Denote the answer by
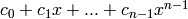 .
.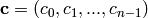 is a codeword in
is a codeword in
 . Every codeword in
. Every codeword in  arises in this way
(from some
arises in this way
(from some 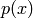 ).
).The polynomial notation for the code is to call
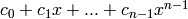 the codeword (instead of
the codeword (instead of
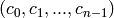 ). The polynomial
). The polynomial
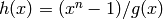 is called the check polynomial of
is called the check polynomial of
 .
.
Let  be a positive integer relatively prime to
be a positive integer relatively prime to
 and let
and let 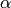 be a primitive
be a primitive
 -th root of unity. Each generator polynomial
-th root of unity. Each generator polynomial 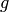 of a cyclic code
of a cyclic code  of length
of length  has a
factorization of the form
has a
factorization of the form
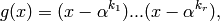
where 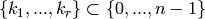 . The
numbers
. The
numbers 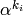 ,
, 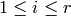 , are
called the zeros of the code
, are
called the zeros of the code  . Many families of cyclic
codes (such as BCH codes and the quadratic residue codes) are
defined using properties of the zeros of
. Many families of cyclic
codes (such as BCH codes and the quadratic residue codes) are
defined using properties of the zeros of  .
.
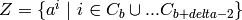 , where
, where
 is a primitive
is a primitive 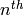 root of unity in the
splitting field
root of unity in the
splitting field 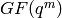 ,
, 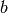 is an integer
is an integer
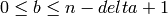 and
and 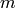 is the multiplicative
order of
is the multiplicative
order of  modulo
modulo  . The default here is
. The default here is 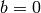 (unlike Guava, which has default
(unlike Guava, which has default 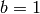 ). Here
). Here 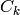 are
the cyclotomic codes (see cyclotomic_cosets).
are
the cyclotomic codes (see cyclotomic_cosets). of order
of order  ,
let
,
let  and
and 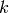 be chosen such that
be chosen such that
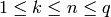 .
Pick
.
Pick  distinct elements of
distinct elements of  , denoted
, denoted
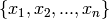 . Then, the codewords are obtained
by evaluating every polynomial in
. Then, the codewords are obtained
by evaluating every polynomial in ![F[x]](../../_images/math/3058cfec73981ccfab32d12bb576d63b2bf97bf6.png) of degree less than
of degree less than
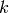 at each
at each 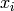 .
.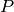 denote a list of lattice points in
denote a list of lattice points in
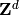 and let
and let 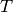 denote a listing of all
points in
denote a listing of all
points in 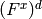 . Put
. Put 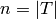 and let
and let 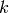 denote the dimension of the vector space of functions
denote the dimension of the vector space of functions
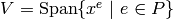 .
The associated toric code
.
The associated toric code  is
the evaluation code which is the image of the evaluation map
is
the evaluation code which is the image of the evaluation map
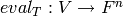 , where
, where 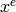 is the
multi-index notation.
is the
multi-index notation.![[2^m,m,2^{m-1}]](../../_images/math/579422ac7aa46b559327fb38307750617de3af33.png) code
related to Hadamard matrices.
http://en.wikipedia.org/wiki/Walsh_code
code
related to Hadamard matrices.
http://en.wikipedia.org/wiki/Walsh_codePlease see the docstrings below for further details.
REFERENCES:
| [HP] | (1, 2, 3, 4, 5, 6, 7, 8, 9) W. C. Huffman, V. Pless, Fundamentals of Error-Correcting Codes, Cambridge Univ. Press, 2003. |
A ‘Bose-Chaudhuri-Hockenghem code’ (or BCH code for short) is the
largest possible cyclic code of length n over field F=GF(q), whose
generator polynomial has zeros (which contain the set)
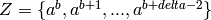 , where a is a
primitive
, where a is a
primitive 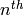 root of unity in the splitting field
root of unity in the splitting field
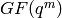 , b is an integer
, b is an integer 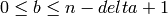 and m is the multiplicative order of q modulo n. (The integers
and m is the multiplicative order of q modulo n. (The integers
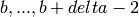 typically lie in the range
typically lie in the range
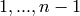 .) The integer
.) The integer 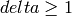 is called
the “designed distance”. The length n of the code and the size q of
the base field must be relatively prime. The generator polynomial
is equal to the least common multiple of the minimal polynomials of
the elements of the set
is called
the “designed distance”. The length n of the code and the size q of
the base field must be relatively prime. The generator polynomial
is equal to the least common multiple of the minimal polynomials of
the elements of the set 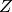 above.
above.
Special cases are b=1 (resulting codes are called ‘narrow-sense’
BCH codes), and 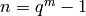 (known as ‘primitive’ BCH
codes).
(known as ‘primitive’ BCH
codes).
It may happen that several values of delta give rise to the same
BCH code. The largest one is called the Bose distance of the code.
The true minimum distance, d, of the code is greater than or equal
to the Bose distance, so 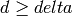 .
.
EXAMPLES:
sage: FF.<a> = GF(3^2,"a")
sage: x = PolynomialRing(FF,"x").gen()
sage: L = [b.minpoly() for b in [a,a^2,a^3]]; g = LCM(L)
sage: f = x^(8)-1
sage: g.divides(f)
True
sage: C = CyclicCode(8,g); C
Linear code of length 8, dimension 4 over Finite Field of size 3
sage: C.minimum_distance()
4
sage: C = BCHCode(8,3,GF(3),1); C
Linear code of length 8, dimension 4 over Finite Field of size 3
sage: C.minimum_distance()
4
sage: C = BCHCode(8,3,GF(3)); C
Linear code of length 8, dimension 5 over Finite Field of size 3
sage: C.minimum_distance()
3
sage: C = BCHCode(26, 5, GF(5), b=1); C
Linear code of length 26, dimension 10 over Finite Field of size 5
BinaryGolayCode() returns a binary Golay code. This is a perfect
[23,12,7] code. It is also (equivalent to) a cyclic code, with
generator polynomial
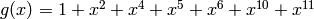 . Extending it yields
the extended Golay code (see ExtendedBinaryGolayCode).
. Extending it yields
the extended Golay code (see ExtendedBinaryGolayCode).
EXAMPLE:
sage: C = BinaryGolayCode()
sage: C
Linear code of length 23, dimension 12 over Finite Field of size 2
sage: C.minimum_distance() # long time
7
AUTHORS:
If g is a polynomial over GF(q) which divides 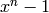 then
this constructs the code “generated by g” (ie, the code associated
with the principle ideal
then
this constructs the code “generated by g” (ie, the code associated
with the principle ideal 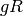 in the ring
in the ring
![R = GF(q)[x]/(x^n-1)](../../_images/math/d9b0db6876da40cff0577dc4afcbd220369fa26e.png) in the usual way).
in the usual way).
The option “ignore” says to ignore the condition that (a) the
characteristic of the base field does not divide the length (the
usual assumption in the theory of cyclic codes), and (b) 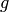 must divide
must divide 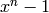 . If ignore=True, instead of returning
an error, a code generated by
. If ignore=True, instead of returning
an error, a code generated by 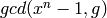 is created.
is created.
EXAMPLES:
sage: P.<x> = PolynomialRing(GF(3),"x")
sage: g = x-1
sage: C = CyclicCodeFromGeneratingPolynomial(4,g); C
Linear code of length 4, dimension 3 over Finite Field of size 3
sage: P.<x> = PolynomialRing(GF(4,"a"),"x")
sage: g = x^3+1
sage: C = CyclicCodeFromGeneratingPolynomial(9,g); C
Linear code of length 9, dimension 6 over Finite Field in a of size 2^2
sage: P.<x> = PolynomialRing(GF(2),"x")
sage: g = x^3+x+1
sage: C = CyclicCodeFromGeneratingPolynomial(7,g); C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C.gen_mat()
[1 1 0 1 0 0 0]
[0 1 1 0 1 0 0]
[0 0 1 1 0 1 0]
[0 0 0 1 1 0 1]
sage: g = x+1
sage: C = CyclicCodeFromGeneratingPolynomial(4,g); C
Linear code of length 4, dimension 3 over Finite Field of size 2
sage: C.gen_mat()
[1 1 0 0]
[0 1 1 0]
[0 0 1 1]
On the other hand, CyclicCodeFromPolynomial(4,x) will produce a
ValueError including a traceback error message: “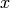 must
divide
must
divide 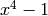 “. You will also get a ValueError if you
type
“. You will also get a ValueError if you
type
sage: P.<x> = PolynomialRing(GF(4,"a"),"x")
sage: g = x^2+1
followed by CyclicCodeFromGeneratingPolynomial(6,g). You will also get a ValueError if you type
sage: P.<x> = PolynomialRing(GF(3),"x")
sage: g = x^2-1
sage: C = CyclicCodeFromGeneratingPolynomial(5,g); C
Linear code of length 5, dimension 4 over Finite Field of size 3
followed by C = CyclicCodeFromGeneratingPolynomial(5,g,False), with
a traceback message including “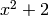 must divide
must divide
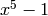 “.
“.
If h is a polynomial over GF(q) which divides 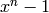 then
this constructs the code “generated by
then
this constructs the code “generated by 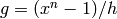 ”
(ie, the code associated with the principle ideal
”
(ie, the code associated with the principle ideal 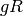 in
the ring
in
the ring ![R = GF(q)[x]/(x^n-1)](../../_images/math/d9b0db6876da40cff0577dc4afcbd220369fa26e.png) in the usual way). The
option “ignore” says to ignore the condition that the
characteristic of the base field does not divide the length (the
usual assumption in the theory of cyclic codes).
in the usual way). The
option “ignore” says to ignore the condition that the
characteristic of the base field does not divide the length (the
usual assumption in the theory of cyclic codes).
EXAMPLES:
sage: P.<x> = PolynomialRing(GF(3),"x")
sage: C = CyclicCodeFromCheckPolynomial(4,x + 1); C
Linear code of length 4, dimension 1 over Finite Field of size 3
sage: C = CyclicCodeFromCheckPolynomial(4,x^3 + x^2 + x + 1); C
Linear code of length 4, dimension 3 over Finite Field of size 3
sage: C.gen_mat()
[2 1 0 0]
[0 2 1 0]
[0 0 2 1]
If g is a polynomial over GF(q) which divides 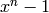 then
this constructs the code “generated by g” (ie, the code associated
with the principle ideal
then
this constructs the code “generated by g” (ie, the code associated
with the principle ideal 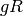 in the ring
in the ring
![R = GF(q)[x]/(x^n-1)](../../_images/math/d9b0db6876da40cff0577dc4afcbd220369fa26e.png) in the usual way).
in the usual way).
The option “ignore” says to ignore the condition that (a) the
characteristic of the base field does not divide the length (the
usual assumption in the theory of cyclic codes), and (b)  must divide
must divide 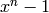 . If ignore=True, instead of returning
an error, a code generated by
. If ignore=True, instead of returning
an error, a code generated by 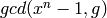 is created.
is created.
EXAMPLES:
sage: P.<x> = PolynomialRing(GF(3),"x")
sage: g = x-1
sage: C = CyclicCodeFromGeneratingPolynomial(4,g); C
Linear code of length 4, dimension 3 over Finite Field of size 3
sage: P.<x> = PolynomialRing(GF(4,"a"),"x")
sage: g = x^3+1
sage: C = CyclicCodeFromGeneratingPolynomial(9,g); C
Linear code of length 9, dimension 6 over Finite Field in a of size 2^2
sage: P.<x> = PolynomialRing(GF(2),"x")
sage: g = x^3+x+1
sage: C = CyclicCodeFromGeneratingPolynomial(7,g); C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C.gen_mat()
[1 1 0 1 0 0 0]
[0 1 1 0 1 0 0]
[0 0 1 1 0 1 0]
[0 0 0 1 1 0 1]
sage: g = x+1
sage: C = CyclicCodeFromGeneratingPolynomial(4,g); C
Linear code of length 4, dimension 3 over Finite Field of size 2
sage: C.gen_mat()
[1 1 0 0]
[0 1 1 0]
[0 0 1 1]
On the other hand, CyclicCodeFromPolynomial(4,x) will produce a
ValueError including a traceback error message: “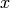 must
divide
must
divide 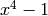 “. You will also get a ValueError if you
type
“. You will also get a ValueError if you
type
sage: P.<x> = PolynomialRing(GF(4,"a"),"x")
sage: g = x^2+1
followed by CyclicCodeFromGeneratingPolynomial(6,g). You will also get a ValueError if you type
sage: P.<x> = PolynomialRing(GF(3),"x")
sage: g = x^2-1
sage: C = CyclicCodeFromGeneratingPolynomial(5,g); C
Linear code of length 5, dimension 4 over Finite Field of size 3
followed by C = CyclicCodeFromGeneratingPolynomial(5,g,False), with
a traceback message including “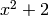 must divide
must divide
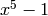 “.
“.
Constructs the “even pair” of duadic codes associated to the “splitting” (see the docstring for is_a_splitting for the definition) S1, S2 of n.
Warning
Maybe the splitting should be associated to a sum of q-cyclotomic cosets mod n, where q is a prime.
EXAMPLES:
sage: from sage.coding.code_constructions import is_a_splitting
sage: n = 11; q = 3
sage: C = cyclotomic_cosets(q,n); C
[[0], [1, 3, 4, 5, 9], [2, 6, 7, 8, 10]]
sage: S1 = C[1]
sage: S2 = C[2]
sage: is_a_splitting(S1,S2,11)
(True, 2)
sage: DuadicCodeEvenPair(GF(q),S1,S2)
(Linear code of length 11, dimension 5 over Finite Field of size 3,
Linear code of length 11, dimension 5 over Finite Field of size 3)
Constructs the “odd pair” of duadic codes associated to the “splitting” S1, S2 of n.
Warning
Maybe the splitting should be associated to a sum of q-cyclotomic cosets mod n, where q is a prime.
EXAMPLES:
sage: from sage.coding.code_constructions import is_a_splitting
sage: n = 11; q = 3
sage: C = cyclotomic_cosets(q,n); C
[[0], [1, 3, 4, 5, 9], [2, 6, 7, 8, 10]]
sage: S1 = C[1]
sage: S2 = C[2]
sage: is_a_splitting(S1,S2,11)
(True, 2)
sage: DuadicCodeOddPair(GF(q),S1,S2)
(Linear code of length 11, dimension 6 over Finite Field of size 3,
Linear code of length 11, dimension 6 over Finite Field of size 3)
This is consistent with Theorem 6.1.3 in [HP].
ExtendedBinaryGolayCode() returns the extended binary Golay code. This is a perfect [24,12,8] code. This code is self-dual.
EXAMPLES:
sage: C = ExtendedBinaryGolayCode()
sage: C
Linear code of length 24, dimension 12 over Finite Field of size 2
sage: C.minimum_distance()
8
AUTHORS:
The extended quadratic residue code (or XQR code) is obtained from a QR code by adding a check bit to the last coordinate. (These codes have very remarkable properties such as large automorphism groups and duality properties - see [HP], Section 6.6.3-6.6.4.)
INPUT:
OUTPUT: Returns an extended quadratic residue code.
EXAMPLES:
sage: C1 = QuadraticResidueCode(7,GF(2))
sage: C2 = C1.extended_code()
sage: C3 = ExtendedQuadraticResidueCode(7,GF(2)); C3
Linear code of length 8, dimension 4 over Finite Field of size 2
sage: C2 == C3
True
sage: C = ExtendedQuadraticResidueCode(17,GF(2))
sage: C
Linear code of length 18, dimension 9 over Finite Field of size 2
sage: C3 = QuadraticResidueCodeOddPair(7,GF(2))[0]
sage: C3x = C3.extended_code()
sage: C4 = ExtendedQuadraticResidueCode(7,GF(2))
sage: C3x == C4
True
AUTHORS:
ExtendedTernaryGolayCode returns a ternary Golay code. This is a self-dual perfect [12,6,6] code.
EXAMPLES:
sage: C = ExtendedTernaryGolayCode()
sage: C
Linear code of length 12, dimension 6 over Finite Field of size 3
sage: C.minimum_distance()
6
AUTHORS:
Implements the Hamming codes.
The 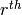 Hamming code over
Hamming code over 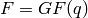 is an
is an
![[n,k,d]](../../_images/math/cc42e8e038862e16c362efb9b3d2b9e56b81091e.png) code with length
code with length 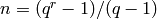 ,
dimension
,
dimension 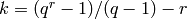 and minimum distance
and minimum distance
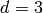 . The parity check matrix of a Hamming code has rows
consisting of all nonzero vectors of length r in its columns,
modulo a scalar factor so no parallel columns arise. A Hamming code
is a single error-correcting code.
. The parity check matrix of a Hamming code has rows
consisting of all nonzero vectors of length r in its columns,
modulo a scalar factor so no parallel columns arise. A Hamming code
is a single error-correcting code.
INPUT:
OUTPUT: Returns the r-th q-ary Hamming code.
EXAMPLES:
sage: HammingCode(3,GF(2))
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C = HammingCode(3,GF(3)); C
Linear code of length 13, dimension 10 over Finite Field of size 3
sage: C.minimum_distance()
3
sage: C = HammingCode(3,GF(4,'a')); C
Linear code of length 21, dimension 18 over Finite Field in a of size 2^2
A linear [n,k]-code C is uniquely determined by its generator matrix G and check matrix H. We have the following short exact sequence
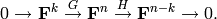
(“Short exact” means (a) the arrow  is injective, i.e.,
is injective, i.e.,
 is a full-rank
is a full-rank 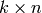 matrix, (b) the
arrow
matrix, (b) the
arrow 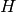 is surjective, and (c)
is surjective, and (c)
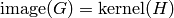 .)
.)
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: H = C.check_mat(); H
[1 0 0 1 1 0 1]
[0 1 0 1 0 1 1]
[0 0 1 1 1 1 0]
sage: LinearCodeFromCheckMatrix(H) == C
True
sage: C = HammingCode(2,GF(3))
sage: H = C.check_mat(); H
[1 0 2 2]
[0 1 2 1]
sage: LinearCodeFromCheckMatrix(H) == C
True
sage: C = RandomLinearCode(10,5,GF(4,"a"))
sage: H = C.check_mat()
sage: LinearCodeFromCheckMatrix(H) == C
True
A quadratic residue code (or QR code) is a cyclic code whose
generator polynomial is the product of the polynomials
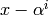 (
(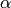 is a primitive
is a primitive
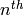 root of unity;
root of unity;  ranges over the set of
quadratic residues modulo
ranges over the set of
quadratic residues modulo  ).
).
See QuadraticResidueCodeEvenPair and QuadraticResidueCodeOddPair for a more general construction.
INPUT:
OUTPUT: Returns a quadratic residue code.
EXAMPLES:
sage: C = QuadraticResidueCode(7,GF(2))
sage: C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C = QuadraticResidueCode(17,GF(2))
sage: C
Linear code of length 17, dimension 9 over Finite Field of size 2
sage: C1 = QuadraticResidueCodeOddPair(7,GF(2))[0]
sage: C2 = QuadraticResidueCode(7,GF(2))
sage: C1 == C2
True
sage: C1 = QuadraticResidueCodeOddPair(17,GF(2))[0]
sage: C2 = QuadraticResidueCode(17,GF(2))
sage: C1 == C2
True
AUTHORS:
Quadratic residue codes of a given odd prime length and base ring either don’t exist at all or occur as 4-tuples - a pair of “odd-like” codes and a pair of “even-like” codes. If n 2 is prime then (Theorem 6.6.2 in [HP]) a QR code exists over GF(q) iff q is a quadratic residue mod n.
They are constructed as “even-like” duadic codes associated the splitting (Q,N) mod n, where Q is the set of non-zero quadratic residues and N is the non-residues.
EXAMPLES:
sage: QuadraticResidueCodeEvenPair(17,GF(13))
(Linear code of length 17, dimension 8 over Finite Field of size 13,
Linear code of length 17, dimension 8 over Finite Field of size 13)
sage: QuadraticResidueCodeEvenPair(17,GF(2))
(Linear code of length 17, dimension 8 over Finite Field of size 2,
Linear code of length 17, dimension 8 over Finite Field of size 2)
sage: QuadraticResidueCodeEvenPair(13,GF(9,"z"))
(Linear code of length 13, dimension 6 over Finite Field in z of size 3^2,
Linear code of length 13, dimension 6 over Finite Field in z of size 3^2)
sage: C1 = QuadraticResidueCodeEvenPair(7,GF(2))[0]
sage: C1.is_self_orthogonal()
True
sage: C2 = QuadraticResidueCodeEvenPair(7,GF(2))[1]
sage: C2.is_self_orthogonal()
True
sage: C3 = QuadraticResidueCodeOddPair(17,GF(2))[0]
sage: C4 = QuadraticResidueCodeEvenPair(17,GF(2))[1]
sage: C3 == C4.dual_code()
True
This is consistent with Theorem 6.6.9 and Exercise 365 in [HP].
Quadratic residue codes of a given odd prime length and base ring either don’t exist at all or occur as 4-tuples - a pair of “odd-like” codes and a pair of “even-like” codes. If n 2 is prime then (Theorem 6.6.2 in [HP]) a QR code exists over GF(q) iff q is a quadratic residue mod n.
They are constructed as “odd-like” duadic codes associated the splitting (Q,N) mod n, where Q is the set of non-zero quadratic residues and N is the non-residues.
EXAMPLES:
sage: QuadraticResidueCodeOddPair(17,GF(13))
(Linear code of length 17, dimension 9 over Finite Field of size 13,
Linear code of length 17, dimension 9 over Finite Field of size 13)
sage: QuadraticResidueCodeOddPair(17,GF(2))
(Linear code of length 17, dimension 9 over Finite Field of size 2,
Linear code of length 17, dimension 9 over Finite Field of size 2)
sage: QuadraticResidueCodeOddPair(13,GF(9,"z"))
(Linear code of length 13, dimension 7 over Finite Field in z of size 3^2,
Linear code of length 13, dimension 7 over Finite Field in z of size 3^2)
sage: C1 = QuadraticResidueCodeOddPair(17,GF(2))[1]
sage: C1x = C1.extended_code()
sage: C2 = QuadraticResidueCodeOddPair(17,GF(2))[0]
sage: C2x = C2.extended_code()
sage: C2x.spectrum(); C1x.spectrum()
[1, 0, 0, 0, 0, 0, 102, 0, 153, 0, 153, 0, 102, 0, 0, 0, 0, 0, 1]
[1, 0, 0, 0, 0, 0, 102, 0, 153, 0, 153, 0, 102, 0, 0, 0, 0, 0, 1]
sage: C2x == C1x.dual_code()
True
sage: C3 = QuadraticResidueCodeOddPair(7,GF(2))[0]
sage: C3x = C3.extended_code()
sage: C3x.spectrum()
[1, 0, 0, 0, 14, 0, 0, 0, 1]
sage: C3x.is_self_dual()
True
This is consistent with Theorem 6.6.14 in [HP].
The method used is to first construct a 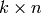 matrix using Sage’s random_element method for the MatrixSpace
class. The construction is probabilistic but should only fail
extremely rarely.
matrix using Sage’s random_element method for the MatrixSpace
class. The construction is probabilistic but should only fail
extremely rarely.
INPUT: Integers n,k, with 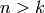 , and a finite field F
, and a finite field F
OUTPUT: Returns a “random” linear code with length n, dimension k over field F.
EXAMPLES:
sage: C = RandomLinearCode(30,15,GF(2))
sage: C
Linear code of length 30, dimension 15 over Finite Field of size 2
sage: C = RandomLinearCode(10,5,GF(4,'a'))
sage: C
Linear code of length 10, dimension 5 over Finite Field in a of size 2^2
AUTHORS:
Given a finite field  of order
of order  , let
, let
 and
and 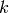 be chosen such that
be chosen such that
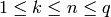 . Pick
. Pick  distinct
elements of
distinct
elements of  , denoted
, denoted
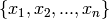 . Then, the codewords are
obtained by evaluating every polynomial in
. Then, the codewords are
obtained by evaluating every polynomial in ![F[x]](../../_images/math/3058cfec73981ccfab32d12bb576d63b2bf97bf6.png) of degree
less than
of degree
less than 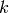 at each
at each 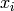 :
:
![C = \left\{ \left( f(x_1), f(x_2), ..., f(x_n) \right), f \in F[x],
{\rm deg}(f)<k \right\}.](../../_images/math/a40dc3b7c74da3c7860545d547d68b71042cb093.png)
 is a
is a ![[n, k, n-k+1]](../../_images/math/2b0ed9826a896c87910053c588a41395552e5715.png) code. (In particular,
code. (In particular,  is MDS.)
is MDS.)
INPUT: n : the length k : the dimension F : the base ring pts : (optional) list of n points in F (if None then Sage picks n of them in the order given to the elements of F)
EXAMPLES:
sage: C = ReedSolomonCode(6,4,GF(7)); C
Linear code of length 6, dimension 4 over Finite Field of size 7
sage: C.minimum_distance()
3
sage: C = ReedSolomonCode(6,4,GF(8,"a")); C
Linear code of length 6, dimension 4 over Finite Field in a of size 2^3
sage: C.minimum_distance()
3
sage: F.<a> = GF(3^2,"a")
sage: pts = [0,1,a,a^2,2*a,2*a+1]
sage: len(Set(pts)) == 6 # to make sure there are no duplicates
True
sage: C = ReedSolomonCode(6,4,F,pts); C
Linear code of length 6, dimension 4 over Finite Field in a of size 3^2
sage: C.minimum_distance()
3
REFERENCES:
TernaryGolayCode returns a ternary Golay code. This is a perfect
[11,6,5] code. It is also equivalent to a cyclic code, with
generator polynomial 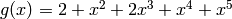 .
.
EXAMPLES:
sage: C = TernaryGolayCode()
sage: C
Linear code of length 11, dimension 6 over Finite Field of size 3
sage: C.minimum_distance()
5
AUTHORS:
Let 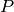 denote a list of lattice points in
denote a list of lattice points in
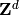 and let
and let 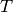 denote the set of all
points in
denote the set of all
points in 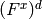 (ordered in some fixed way). Put
(ordered in some fixed way). Put
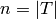 and let
and let 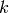 denote the dimension of the
vector space of functions
denote the dimension of the
vector space of functions 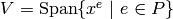 .
The associated toric code
.
The associated toric code  is the evaluation code which
is the image of the evaluation map
is the evaluation code which
is the image of the evaluation map
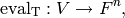
where 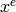 is the multi-index notation
(
is the multi-index notation
(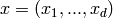 ,
, 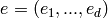 , and
, and
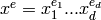 ), where
), where
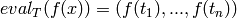 , and where
, and where
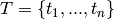 . This function returns the toric
codes discussed in [J].
. This function returns the toric
codes discussed in [J].
INPUT:
OUTPUT: Returns toric code with length n = , dimension k over field F.
EXAMPLES:
sage: C = ToricCode([[0,0],[1,0],[2,0],[0,1],[1,1]],GF(7))
sage: C
Linear code of length 36, dimension 5 over Finite Field of size 7
sage: C.minimum_distance()
24
sage: C = ToricCode([[-2,-2],[-1,-2],[-1,-1],[-1,0],[0,-1],[0,0],[0,1],[1,-1],[1,0]],GF(5))
sage: C
Linear code of length 16, dimension 9 over Finite Field of size 5
sage: C.minimum_distance()
6
sage: C = ToricCode([ [0,0],[1,1],[1,2],[1,3],[1,4],[2,1],[2,2],[2,3],[3,1],[3,2],[4,1]],GF(8,"a"))
sage: C
Linear code of length 49, dimension 11 over Finite Field in a of size 2^3
This is in fact a [49,11,28] code over GF(8). If you type next C.minimum_distance() and wait overnight (!), you should get 28.
AUTHOR:
REFERENCES:
| [J] | D. Joyner, Toric codes over finite fields, Applicable Algebra in Engineering, Communication and Computing, 15, (2004), p. 63-79. |
Returns the binary Walsh code of length 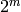 . The matrix
of codewords correspond to a Hadamard matrix. This is a (constant
rate) binary linear
. The matrix
of codewords correspond to a Hadamard matrix. This is a (constant
rate) binary linear ![[2^m,m,2^{m-1}]](../../_images/math/579422ac7aa46b559327fb38307750617de3af33.png) code.
code.
EXAMPLES:
sage: C = WalshCode(4); C
Linear code of length 16, dimension 4 over Finite Field of size 2
sage: C = WalshCode(3); C
Linear code of length 8, dimension 3 over Finite Field of size 2
sage: C.spectrum()
[1, 0, 0, 0, 7, 0, 0, 0, 0]
REFERENCES:
INPUT: q,n,t positive integers (or t=None) Some type-checking of inputs is performed.
OUTPUT: q-cyclotomic cosets mod n (or, if t is not None, the q-cyclotomic coset mod n containing t)
Let q, n be relatively print positive integers and let
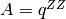 . The group A acts on ZZ/nZZ by multiplication.
The orbits of this action are “cyclotomic cosets”, or more
precisely “q-cyclotomic cosets mod n”. Sometimes the smallest
element of the coset is called the “coset leader”. The algorithm
will always return the cosets as sorted lists of lists, so the
coset leader will always be the first element in the list.
. The group A acts on ZZ/nZZ by multiplication.
The orbits of this action are “cyclotomic cosets”, or more
precisely “q-cyclotomic cosets mod n”. Sometimes the smallest
element of the coset is called the “coset leader”. The algorithm
will always return the cosets as sorted lists of lists, so the
coset leader will always be the first element in the list.
These cosets arise in the theory of duadic codes and minimal
polynomials of finite fields. Fix a primitive element  of
of 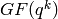 . The minimal polynomial of
. The minimal polynomial of 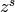 over
over
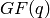 is given by
is given by
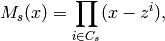
where 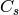 is the q-cyclotomic coset mod n containing s,
is the q-cyclotomic coset mod n containing s,
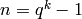 .
.
EXAMPLES:
sage: cyclotomic_cosets(2,11)
[[0], [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]
sage: cyclotomic_cosets(2,15)
[[0], [1, 2, 4, 8], [3, 6, 9, 12], [5, 10], [7, 11, 13, 14]]
sage: cyclotomic_cosets(2,15,5)
[5, 10]
sage: cyclotomic_cosets(3,16)
[[0], [1, 3, 9, 11], [2, 6], [4, 12], [5, 7, 13, 15], [8], [10, 14]]
sage: F.<z> = GF(2^4, "z")
sage: P.<x> = PolynomialRing(F,"x")
sage: a = z^5
sage: a.minimal_polynomial()
x^2 + x + 1
sage: prod([x-z^i for i in [5, 10]])
x^2 + x + 1
sage: cyclotomic_cosets(3,2,0)
[0]
sage: cyclotomic_cosets(3,2,1)
[1]
sage: cyclotomic_cosets(3,2,2)
[0]
This last output looks strange but is correct, since the elements of the cosets are in ZZ/nZZ and 2 = 0 in ZZ/2ZZ.
INPUT: S1, S2 are disjoint sublists partitioning [1, 2, ..., n-1] n1 is an integer
OUTPUT: a, b where a is True or False, depending on whether S1, S2 form a “splitting” of n (ie, if there is a b1 such that b*S1=S2 (point-wise multiplication mod n), and b is a splitting (if a = True) or 0 (if a = False)
Splittings are useful for computing idempotents in the quotient
ring ![Q = GF(q)[x]/(x^n-1)](../../_images/math/5931375a0a48e1858ea9ad1420800c5acfeefc6e.png) . For
. For
EXAMPLES:
sage: from sage.coding.code_constructions import is_a_splitting
sage: n = 11; q = 3
sage: C = cyclotomic_cosets(q,n); C
[[0], [1, 3, 4, 5, 9], [2, 6, 7, 8, 10]]
sage: S1 = C[1]
sage: S2 = C[2]
sage: is_a_splitting(S1,S2,11)
(True, 2)
sage: F = GF(q)
sage: P.<x> = PolynomialRing(F,"x")
sage: I = Ideal(P,[x^n-1])
sage: Q.<x> = QuotientRing(P,I)
sage: i1 = -sum([x^i for i in S1]); i1
2*x^9 + 2*x^5 + 2*x^4 + 2*x^3 + 2*x
sage: i2 = -sum([x^i for i in S2]); i2
2*x^10 + 2*x^8 + 2*x^7 + 2*x^6 + 2*x^2
sage: i1^2 == i1
True
sage: i2^2 == i2
True
sage: (1-i1)^2 == 1-i1
True
sage: (1-i2)^2 == 1-i2
True
We return to dealing with polynomials (rather than elements of quotient rings), so we can construct cyclic codes:
sage: P.<x> = PolynomialRing(F,"x")
sage: i1 = -sum([x^i for i in S1])
sage: i2 = -sum([x^i for i in S2])
sage: i1_sqrd = (i1^2).quo_rem(x^n-1)[1]
sage: i1_sqrd == i1
True
sage: i2_sqrd = (i2^2).quo_rem(x^n-1)[1]
sage: i2_sqrd == i2
True
sage: C1 = CyclicCodeFromGeneratingPolynomial(n,i1)
sage: C2 = CyclicCodeFromGeneratingPolynomial(n,1-i2)
sage: C1.dual_code() == C2
True
This is a special case of Theorem 6.4.3 in [HP].
INPUT: a is an element of a finite field GF(q)
OUTPUT: the element b of the smallest subfield F of GF(q) for which F(b)=a.
EXAMPLES:
sage: from sage.coding.code_constructions import lift2smallest_field
sage: FF.<z> = GF(3^4,"z")
sage: a = z^10
sage: lift2smallest_field(a)
(2*z + 1, Finite Field in z of size 3^2)
sage: a = z^40
sage: lift2smallest_field(a)
(2, Finite Field of size 3)
AUTHORS:
INPUT: a is an element of a finite field GF(q) OUTPUT: the element b of the smallest subfield F of GF(q) for which F(b)=a.
EXAMPLES:
sage: from sage.coding.code_constructions import lift2smallest_field2
sage: FF.<z> = GF(3^4,"z")
sage: a = z^40
sage: lift2smallest_field2(a)
(2, Finite Field of size 3)
sage: FF.<z> = GF(2^4,"z")
sage: a = z^15
sage: lift2smallest_field2(a)
(1, Finite Field of size 2)
Warning
Since coercion (the FF(b) step) has a bug in it, this only works in the case when you know F is a prime field.
AUTHORS:
Returns permutation of rows g*v. Works on lists, matrices, sequences and vectors (by permuting coordinates). The code requires switching from i to i+1 (and back again) since the SymmetricGroup is, by convention, the symmetric group on the “letters” 1, 2, ..., n (not 0, 1, ..., n-1).
EXAMPLES:
sage: V = VectorSpace(GF(3),5)
sage: v = V([0,1,2,0,1])
sage: G = SymmetricGroup(5)
sage: g = G([(1,2,3)])
sage: permutation_action(g,v)
(1, 2, 0, 0, 1)
sage: g = G([()])
sage: permutation_action(g,v)
(0, 1, 2, 0, 1)
sage: g = G([(1,2,3,4,5)])
sage: permutation_action(g,v)
(1, 2, 0, 1, 0)
sage: L = Sequence([1,2,3,4,5])
sage: permutation_action(g,L)
[2, 3, 4, 5, 1]
sage: MS = MatrixSpace(GF(3),3,7)
sage: A = MS([[1,0,0,0,1,1,0],[0,1,0,1,0,1,0],[0,0,0,0,0,0,1]])
sage: S5 = SymmetricGroup(5)
sage: g = S5([(1,2,3)])
sage: A
[1 0 0 0 1 1 0]
[0 1 0 1 0 1 0]
[0 0 0 0 0 0 1]
sage: permutation_action(g,A)
[0 1 0 1 0 1 0]
[0 0 0 0 0 0 1]
[1 0 0 0 1 1 0]
It also works on lists and is a “left action”:
sage: v = [0,1,2,0,1]
sage: G = SymmetricGroup(5)
sage: g = G([(1,2,3)])
sage: gv = permutation_action(g,v); gv
[1, 2, 0, 0, 1]
sage: permutation_action(g,v) == g(v)
True
sage: h = G([(3,4)])
sage: gv = permutation_action(g,v)
sage: hgv = permutation_action(h,gv)
sage: hgv == permutation_action(h*g,v)
True
AUTHORS:
This is the generator matrix of a Walsh code. The matrix of codewords correspond to a Hadamard matrix.
EXAMPLES:
sage: walsh_matrix(2)
[0 0 1 1]
[0 1 0 1]
sage: walsh_matrix(3)
[0 0 0 0 1 1 1 1]
[0 0 1 1 0 0 1 1]
[0 1 0 1 0 1 0 1]
sage: C = LinearCode(walsh_matrix(4)); C
Linear code of length 16, dimension 4 over Finite Field of size 2
sage: C.spectrum()
[1, 0, 0, 0, 0, 0, 0, 0, 15, 0, 0, 0, 0, 0, 0, 0, 0]
This last code has minimum distance 8.
REFERENCES: