Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Coding Theory »
This module provided some upper and lower bounds for the parameters of codes.
AUTHORS:
Let 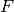 be a finite field (we denote the finite field with
be a finite field (we denote the finite field with
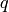 elements by
elements by 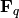 ).
A subset
).
A subset 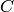 of
of 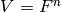 is called a code of
length
is called a code of
length  . A subspace of
. A subspace of 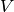 (with the standard
basis) is called a linear code of length
(with the standard
basis) is called a linear code of length  . If its
dimension is denoted
. If its
dimension is denoted  then we typically store a basis of
then we typically store a basis of
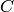 as a
as a 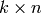 matrix (the rows are the basis
vectors). If
matrix (the rows are the basis
vectors). If  then
then 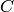 is
called a binary code. If
is
called a binary code. If 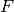 has
has 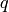 elements
then
elements
then 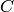 is called a
is called a 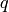 -ary code. The elements
of a code
-ary code. The elements
of a code 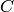 are called codewords. The information rate
of
are called codewords. The information rate
of 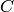 is
is
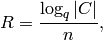
where  denotes the number of elements of
denotes the number of elements of
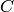 . If
. If 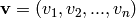 ,
,
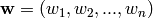 are vectors in
are vectors in
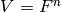 then we define
then we define
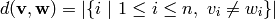
to be the Hamming distance between 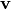 and
and
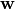 . The function
. The function
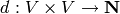 is called the Hamming
metric. The weight of a vector (in the Hamming metric) is
is called the Hamming
metric. The weight of a vector (in the Hamming metric) is
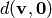 . The minimum distance of a linear
code is the smallest non-zero weight of a codeword in
. The minimum distance of a linear
code is the smallest non-zero weight of a codeword in 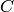 .
The relatively minimum distance is denoted
.
The relatively minimum distance is denoted
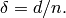
A linear code with length
 , dimension
, dimension  , and minimum distance
, and minimum distance
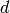 is called an
is called an ![[n,k,d]_q](../../_images/math/85ae31d242623378b682627429f58ba95526db0f.png) -code and
-code and
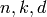 are called its parameters. A (not necessarily
linear) code
are called its parameters. A (not necessarily
linear) code 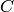 with length
with length  , size
, size
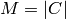 , and minimum distance
, and minimum distance 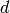 is called an
is called an
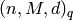 -code (using parentheses instead of square
brackets). Of course,
-code (using parentheses instead of square
brackets). Of course, 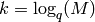 for linear codes.
for linear codes.
What is the “best” code of a given length? Let 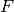 be a
finite field with
be a
finite field with 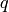 elements. Let
elements. Let 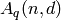 denote the largest
denote the largest 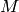 such that there exists a
such that there exists a
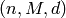 code in
code in 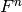 . Let
. Let  (also denoted
(also denoted  ) denote the largest
) denote the largest
 such that there exists a
such that there exists a ![[n,k,d]](../../_images/math/cc42e8e038862e16c362efb9b3d2b9e56b81091e.png) code in
code in
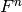 . (Of course,
. (Of course,  .)
Determining
.)
Determining 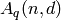 and
and  is one of
the main problems in the theory of error-correcting codes.
is one of
the main problems in the theory of error-correcting codes.
These quantities related to solving a generalization of the childhood game of “20 questions”.
GAME: Player 1 secretly chooses a number from  to
to
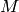 (
(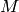 is large but fixed). Player 2 asks a
series of “yes/no questions” in an attempt to determine that
number. Player 1 may lie at most
is large but fixed). Player 2 asks a
series of “yes/no questions” in an attempt to determine that
number. Player 1 may lie at most  times
(
times
(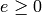 is fixed). What is the minimum number of “yes/no
questions” Player 2 must ask to (always) be able to correctly
determine the number Player 1 chose?
is fixed). What is the minimum number of “yes/no
questions” Player 2 must ask to (always) be able to correctly
determine the number Player 1 chose?
If feedback is not allowed (the only situation considered here),
call this minimum number 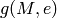 .
.
Lemma: For fixed  and
and 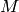 ,
, 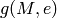 is
the smallest
is
the smallest  such that
such that 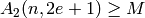 .
.
Thus, solving the solving a generalization of the game of “20
questions” is equivalent to determining  ! Using
Sage, you can determine the best known estimates for this number in
2 ways:
! Using
Sage, you can determine the best known estimates for this number in
2 ways:
(1) Indirectly, using minimum_distance_lower_bound(n,k,F) and minimum_distance_upper_bound(n,k,F) (both of which which connect to the internet using Steven Sivek’s linear_code_bound(q,n,k)) (2) codesize_upper_bound(n,d,q), dimension_upper_bound(n,d,q).
This module implements:
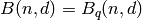 for the dimension of a linear code of
length n, minimum distance d over a field of size q.
for the dimension of a linear code of
length n, minimum distance d over a field of size q.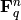 .
.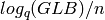 , where GLB is
the Gilbert lower bound and delta = d/n.
, where GLB is
the Gilbert lower bound and delta = d/n.PROBLEM: In this module we shall typically either (a) seek bounds on k, given n, d, q, (b) seek bounds on R, delta, q (assuming n is “infinity”).
TODO:
REFERENCES:
This computes the minimum value of the upper bound using the methods of Singleton, Hamming, Plotkin and Elias.
If method=”gap” then this returns the best known upper
bound 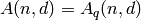 for the size of a code of length n,
minimum distance d over a field of size q. The function first
checks for trivial cases (like d=1 or n=d), and if the value
is in the built-in table. Then it calculates the minimum value
of the upper bound using the methods of Singleton, Hamming,
Johnson, Plotkin and Elias. If the code is binary,
for the size of a code of length n,
minimum distance d over a field of size q. The function first
checks for trivial cases (like d=1 or n=d), and if the value
is in the built-in table. Then it calculates the minimum value
of the upper bound using the methods of Singleton, Hamming,
Johnson, Plotkin and Elias. If the code is binary,
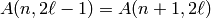 , so the function
takes the minimum of the values obtained from all methods for the
parameters
, so the function
takes the minimum of the values obtained from all methods for the
parameters  and
and 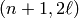 . This
wraps GUAVA’s UpperBound( n, d, q ).
. This
wraps GUAVA’s UpperBound( n, d, q ).
Returns an upper bound 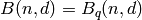 for the
dimension of a linear code of length n, minimum distance d over a
field of size q.
for the
dimension of a linear code of length n, minimum distance d over a
field of size q.
EXAMPLES:
sage: dimension_upper_bound(10,3,2)
6
Computes the asymptotic Elias bound for the information rate,
provided 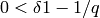 .
.
EXAMPLES:
sage: elias_bound_asymp(1/4,2)
0.39912396330...
Returns the Elias upper bound for number of elements in the largest
code of minimum distance d in 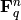 . Wraps
GAP’s UpperBoundElias.
. Wraps
GAP’s UpperBoundElias.
EXAMPLES:
sage: elias_upper_bound(10,2,3)
232
sage: elias_upper_bound(10,2,3,method="gap") # requires optional GAP package Guava
232
Returns lower bound for number of elements in the largest code of
minimum distance d in 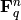 .
.
EXAMPLES:
sage: gilbert_lower_bound(10,2,3)
128/7
Returns the Griesmer upper bound for number of elements in the
largest code of minimum distance d in 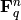 .
Wraps GAP’s UpperBoundGriesmer.
.
Wraps GAP’s UpperBoundGriesmer.
Computes the asymptotic GV bound for the information rate, R.
GV lower bound for information rate of a q-ary code of length n minimum distance delta*n
EXAMPLES:
sage: RDF(gv_info_rate(100,1/4,3))
0.367049926083
Computes the asymptotic Hamming bound for the information rate.
Returns the Hamming upper bound for number of elements in the
largest code of minimum distance d in 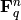 .
Wraps GAP’s UpperBoundHamming.
.
Wraps GAP’s UpperBoundHamming.
The Hamming bound (also known as the sphere packing bound) returns
an upper bound on the size of a code of length n, minimum distance
d, over a field of size q. The Hamming bound is obtained by
dividing the contents of the entire space
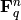 by the contents of a ball with radius
floor((d-1)/2). As all these balls are disjoint, they can never
contain more than the whole vector space.
by the contents of a ball with radius
floor((d-1)/2). As all these balls are disjoint, they can never
contain more than the whole vector space.
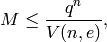
where M is the maximum number of codewords and  is
equal to the contents of a ball of radius e. This bound is useful
for small values of d. Codes for which equality holds are called
perfect.
is
equal to the contents of a ball of radius e. This bound is useful
for small values of d. Codes for which equality holds are called
perfect.
EXAMPLES:
sage: hamming_upper_bound(10,2,3)
93
Computes the first asymptotic McEliese-Rumsey-Rodemich-Welsh bound
for the information rate, provided 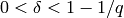 .
.
EXAMPLES:
sage: mrrw1_bound_asymp(1/4,2)
0.354578902665
Computes the asymptotic Plotkin bound for the information rate,
provided 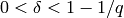 .
.
EXAMPLES:
sage: plotkin_bound_asymp(1/4,2)
1/2
Returns Plotkin upper bound for number of elements in the largest
code of minimum distance d in 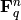 .
.
The method=”gap” option wraps Guava’s UpperBoundPlotkin.
Computes the asymptotic Singleton bound for the information rate.
Returns the Singleton upper bound for number of elements in the
largest code of minimum distance d in 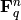 .
Wraps GAP’s UpperBoundSingleton.
.
Wraps GAP’s UpperBoundSingleton.
This bound is based on the shortening of codes. By shortening an
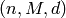 code d-1 times, an
code d-1 times, an 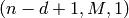 code
results, with
code
results, with 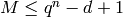 . Thus
. Thus
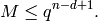
Codes that meet this bound are called maximum distance separable (MDS).
Returns number of elements in a Hamming ball of radius r in 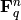 .
Agrees with Guava’s SphereContent(n,r,GF(q)).
.
Agrees with Guava’s SphereContent(n,r,GF(q)).
EXAMPLES:
sage: volume_hamming(10,2,3)
176