Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Coding Theory »

VERSION: 1.2
Let  be a finite field. Here, we will denote the finite field with
be a finite field. Here, we will denote the finite field with  elements by
elements by 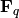 . A subspace of
. A subspace of 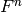 (with the standard basis) is
called a linear code of length
(with the standard basis) is
called a linear code of length  . If its dimension is denoted
. If its dimension is denoted 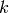 then we
typically store a basis of
then we
typically store a basis of  as a
as a 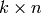 matrix, with rows the basis
vectors. It is called the generator matrix of
matrix, with rows the basis
vectors. It is called the generator matrix of  . The rows of the parity
check matrix of
. The rows of the parity
check matrix of  are a basis for the code,
are a basis for the code,
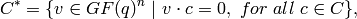
called the dual space of  .
.
If 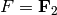 then
then  is called a binary code. If
is called a binary code. If 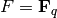 then
then  is
called a
is
called a  -ary code. The elements of a code
-ary code. The elements of a code  are called codewords.
are called codewords.
The symmetric group 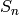 acts on
acts on 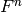 by permuting coordinates. If an
element
by permuting coordinates. If an
element 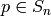 sends a code
sends a code  of length
of length  to itself (in other words,
every codeword of
to itself (in other words,
every codeword of  is sent to some other codeword of
is sent to some other codeword of  ) then
) then  is
called a permutation automorphism of
is
called a permutation automorphism of  . The (permutation) automorphism
group is denoted
. The (permutation) automorphism
group is denoted 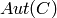 .
.
This file contains
EXAMPLES:
sage: MS = MatrixSpace(GF(2),4,7)
sage: G = MS([[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C.basis()
[(1, 1, 1, 0, 0, 0, 0),
(1, 0, 0, 1, 1, 0, 0),
(0, 1, 0, 1, 0, 1, 0),
(1, 1, 0, 1, 0, 0, 1)]
sage: c = C.basis()[1]
sage: c in C
True
sage: c.nonzero_positions()
[0, 3, 4]
sage: c.support()
[0, 3, 4]
sage: c.parent()
Vector space of dimension 7 over Finite Field of size 2
To be added:
 Goppa codes and group actions on
Goppa codes and group actions on 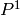 RR space codes.
RR space codes.REFERENCES:
AUTHORS:
TESTS:
sage: MS = MatrixSpace(GF(2),4,7)
sage: G = MS([[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C == loads(dumps(C))
True
Bases: sage.modules.module.Module
A class for linear codes over a finite field or finite ring. Each instance
is a linear code determined by a generator matrix  (i.e., a
(i.e., a
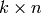 matrix of (full) rank
matrix of (full) rank 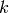 ,
, 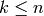 over a finite field
over a finite field  .
.
INPUT:
 . (G can be defined over a
finite ring but the matrices over that ring must have certain
attributes, such as rank.)
. (G can be defined over a
finite ring but the matrices over that ring must have certain
attributes, such as rank.)OUTPUT:
The linear code of length  over
over  having
having  as a generator matrix.
as a generator matrix.
EXAMPLES:
sage: MS = MatrixSpace(GF(2),4,7)
sage: G = MS([[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C.base_ring()
Finite Field of size 2
sage: C.dimension()
4
sage: C.length()
7
sage: C.minimum_distance()
3
sage: C.spectrum()
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C.weight_distribution()
[1, 0, 0, 7, 7, 0, 0, 1]
sage: MS = MatrixSpace(GF(5),4,7)
sage: G = MS([[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C
Linear code of length 7, dimension 4 over Finite Field of size 5
AUTHORS:
Assmus and Mattson Theorem (section 8.4, page 303 of [HP]): Let
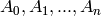 be the weights of the codewords in a binary
linear
be the weights of the codewords in a binary
linear ![[n , k, d]](../../_images/math/959a01265f6aadf1d406ff2f7c35e28a0782285f.png) code
code  , and let
, and let 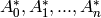 be
the weights of the codewords in its dual
be
the weights of the codewords in its dual ![[n, n-k, d^*]](../../_images/math/05c5e3319dbe25599edf1a32b37252641fb4c943.png) code
code 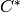 .
Fix a
.
Fix a 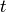 ,
, 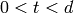 , and let
, and let
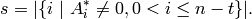
Assume 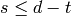 .
.
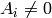 and
and 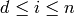 then
then 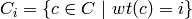 holds a simple t-design.
holds a simple t-design.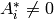 and
and 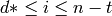 then
then
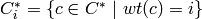 holds a simple t-design.
holds a simple t-design.A block design is a pair 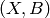 , where
, where  is a non-empty finite set
of
is a non-empty finite set
of 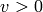 elements called points, and
elements called points, and 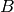 is a non-empty finite
multiset of size b whose elements are called blocks, such that each
block is a non-empty finite multiset of
is a non-empty finite
multiset of size b whose elements are called blocks, such that each
block is a non-empty finite multiset of 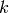 points.
points. 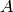 design without
repeated blocks is called a simple block design. If every subset of
points of size
design without
repeated blocks is called a simple block design. If every subset of
points of size 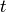 is contained in exactly
is contained in exactly 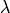 blocks the block
design is called a
blocks the block
design is called a 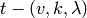 design (or simply a
design (or simply a 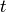 -design
when the parameters are not specified). When
-design
when the parameters are not specified). When 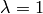 then the
block design is called a
then the
block design is called a 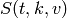 Steiner system.
Steiner system.
In the Assmus and Mattson Theorem (1),  is the set
is the set 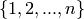 of coordinate locations and
of coordinate locations and 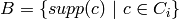 is the set
of supports of the codewords of
is the set
of supports of the codewords of  of weight
of weight  . Therefore, the
parameters of the
. Therefore, the
parameters of the 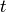 -design for
-design for 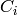 are
are
t = given
v = n
k = i (k not to be confused with dim(C))
b = Ai
lambda = b*binomial(k,t)/binomial(v,t) (by Theorem 8.1.6,
p 294, in [HP])
Setting the mode="verbose" option prints out the values of the parameters.
The first example below means that the binary [24,12,8]-code C has
the property that the (support of the) codewords of weight 8 (resp.,
12, 16) form a 5-design. Similarly for its dual code 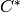 (of course
(of course
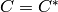 in this case, so this info is extraneous). The test fails to
produce 6-designs (ie, the hypotheses of the theorem fail to hold,
not that the 6-designs definitely don’t exist). The command
assmus_mattson_designs(C,5,mode=”verbose”) returns the same value
but prints out more detailed information.
in this case, so this info is extraneous). The test fails to
produce 6-designs (ie, the hypotheses of the theorem fail to hold,
not that the 6-designs definitely don’t exist). The command
assmus_mattson_designs(C,5,mode=”verbose”) returns the same value
but prints out more detailed information.
The second example below illustrates the blocks of the 5-(24, 8, 1) design (i.e., the S(5,8,24) Steiner system).
EXAMPLES:
sage: C = ExtendedBinaryGolayCode() # example 1
sage: C.assmus_mattson_designs(5)
['weights from C: ',
[8, 12, 16, 24],
'designs from C: ',
[[5, (24, 8, 1)], [5, (24, 12, 48)], [5, (24, 16, 78)], [5, (24, 24, 1)]],
'weights from C*: ',
[8, 12, 16],
'designs from C*: ',
[[5, (24, 8, 1)], [5, (24, 12, 48)], [5, (24, 16, 78)]]]
sage: C.assmus_mattson_designs(6)
0
sage: X = range(24) # example 2
sage: blocks = [c.support() for c in C if hamming_weight(c)==8]; len(blocks) # long time computation
759
REFERENCE:
This only applies to linear binary codes and returns its (permutation)
automorphism group. In other words, if the code  has length
has length  then it returns the subgroup of the symmetric group
then it returns the subgroup of the symmetric group 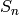 :
:
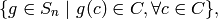
where 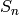 acts on
acts on 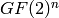 by permuting coordinates.
by permuting coordinates.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: G = C.automorphism_group_binary_code(); G
Permutation Group with generators [(3,4)(5,6), (3,5)(4,6), (2,3)(5,7), (1,2)(5,6)]
sage: G.order()
168
Returns the i-th binomial moment of the ![[n,k,d]_q](../../_images/math/85ae31d242623378b682627429f58ba95526db0f.png) -code
-code  :
:
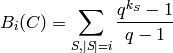
where 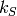 is the dimension of the shortened code
is the dimension of the shortened code 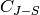 ,
,
![J=[1,2,...,n]](../../_images/math/156fef711b14cfea34404b0a4ab9685923286075.png) . (The normalized binomial moment is
. (The normalized binomial moment is
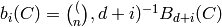 .) In other words,
.) In other words, 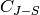 is isomorphic to the subcode of C of codewords supported on S.
is isomorphic to the subcode of C of codewords supported on S.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.binomial_moment(2)
0
sage: C.binomial_moment(4) # long time
35
Warning
This is slow.
REFERENCE:
Returns the characteristic polynomial of a linear code, as defined in van Lint’s text [vL].
EXAMPLES:
sage: C = ExtendedBinaryGolayCode()
sage: C.characteristic_polynomial()
-4/3*x^3 + 64*x^2 - 2816/3*x + 4096
REFERENCES:
Returns the check matrix of self.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: Cperp = C.dual_code()
sage: C; Cperp
Linear code of length 7, dimension 4 over Finite Field of size 2
Linear code of length 7, dimension 3 over Finite Field of size 2
sage: C.gen_mat()
[1 0 0 1 0 1 0]
[0 1 0 1 0 1 1]
[0 0 1 1 0 0 1]
[0 0 0 0 1 1 1]
sage: C.check_mat()
[1 0 0 1 1 0 1]
[0 1 0 1 0 1 1]
[0 0 1 1 1 1 0]
sage: Cperp.check_mat()
[1 0 0 1 0 1 0]
[0 1 0 1 0 1 1]
[0 0 1 1 0 0 1]
[0 0 0 0 1 1 1]
sage: Cperp.gen_mat()
[1 0 0 1 1 0 1]
[0 1 0 1 0 1 1]
[0 0 1 1 1 1 0]
Returns the Chinen zeta polynomial of the code.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.chinen_polynomial() # long time
1/5*(2*sqrt(2)*t^3 + 2*sqrt(2)*t^2 + 2*t^2 + sqrt(2)*t + 2*t + 1)/(sqrt(2) + 1)
sage: C = TernaryGolayCode()
sage: C.chinen_polynomial() # long time
1/7*(3*sqrt(3)*t^3 + 3*sqrt(3)*t^2 + 3*t^2 + sqrt(3)*t + 3*t + 1)/(sqrt(3) + 1)
This last output agrees with the corresponding example given in Chinen’s paper below.
REFERENCES:
Wraps Guava’s CoveringRadius command.
The covering radius of a linear code  is the smallest number
is the smallest number  with the property that each element
with the property that each element  of the ambient vector space
of
of the ambient vector space
of  has at most a distance
has at most a distance  to the code
to the code  . So for each
vector
. So for each
vector  there must be an element
there must be an element  of
of  with
with 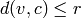 .
A binary linear code with reasonable small covering radius is often
referred to as a covering code.
.
A binary linear code with reasonable small covering radius is often
referred to as a covering code.
For example, if  is a perfect code, the covering radius is equal
to
is a perfect code, the covering radius is equal
to 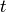 , the number of errors the code can correct, where
, the number of errors the code can correct, where 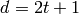 ,
with
,
with 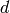 the minimum distance of
the minimum distance of  .
.
EXAMPLES:
sage: C = HammingCode(5,GF(2))
sage: C.covering_radius() # requires optional GAP package Guava
1
Decodes the received vector right to an element  in this code.
in this code.
Optional methods are “guava”, “nearest neighbor” or “syndrome”. The method="guava" wraps GUAVA’s Decodeword. Hamming codes have a special decoding algorithm; otherwise, "syndrome" decoding is used.
INPUT:
OUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: MS = MatrixSpace(GF(2),1,7)
sage: F = GF(2); a = F.gen()
sage: v1 = [a,a,F(0),a,a,F(0),a]
sage: C.decode(v1)
(1, 0, 0, 1, 1, 0, 1)
sage: C.decode(v1,method="nearest neighbor")
(1, 0, 0, 1, 1, 0, 1)
sage: C.decode(v1,method="guava") # requires optional GAP package Guava
(1, 0, 0, 1, 1, 0, 1)
sage: v2 = matrix([[a,a,F(0),a,a,F(0),a]])
sage: C.decode(v2)
(1, 0, 0, 1, 1, 0, 1)
sage: v3 = vector([a,a,F(0),a,a,F(0),a])
sage: c = C.decode(v3); c
(1, 0, 0, 1, 1, 0, 1)
sage: c in C
True
sage: C = HammingCode(2,GF(5))
sage: v = vector(GF(5),[1,0,0,2,1,0])
sage: C.decode(v)
(2, 0, 0, 2, 1, 0)
sage: F = GF(4,"a")
sage: C = HammingCode(2,F)
sage: v = vector(F, [1,0,0,a,1])
sage: C.decode(v)
(1, 0, 0, 1, 1)
sage: C.decode(v, method="nearest neighbor")
(1, 0, 0, 1, 1)
sage: C.decode(v, method="guava") # requires optional GAP package Guava
(1, 0, 0, 1, 1)
Does not work for very long codes since the syndrome table grows too large.
Returns the dimension of this code.
EXAMPLES:
sage: G = matrix(GF(2),[[1,0,0],[1,1,0]])
sage: C = LinearCode(G)
sage: C.dimension()
2
Returns the code given by the direct sum of the codes self and other, which must be linear codes defined over the same base ring.
EXAMPLES:
sage: C1 = HammingCode(3,GF(2))
sage: C2 = C1.direct_sum(C1); C2
Linear code of length 14, dimension 8 over Finite Field of size 2
sage: C3 = C1.direct_sum(C2); C3
Linear code of length 21, dimension 12 over Finite Field of size 2
Returns the divisor of a code, which is the smallest integer 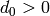 such that each
such that each 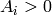 iff
iff  is divisible by
is divisible by 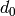 .
.
EXAMPLES:
sage: C = ExtendedBinaryGolayCode()
sage: C.divisor() # Type II self-dual
4
sage: C = QuadraticResidueCodeEvenPair(17,GF(2))[0]
sage: C.divisor()
2
This computes the dual code 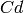 of the code
of the code  ,
,
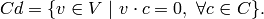
Does not call GAP.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.dual_code()
Linear code of length 7, dimension 3 over Finite Field of size 2
sage: C = HammingCode(3,GF(4,'a'))
sage: C.dual_code()
Linear code of length 21, dimension 3 over Finite Field in a of size 2^2
If self is a linear code of length  defined over
defined over  then this
returns the code of length
then this
returns the code of length 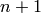 where the last digit
where the last digit 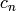 satisfies
the check condition
satisfies
the check condition 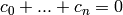 . If self is an
. If self is an ![[n,k,d]](../../_images/math/cc42e8e038862e16c362efb9b3d2b9e56b81091e.png) binary code then the extended code
binary code then the extended code 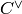 is an
is an ![[n+1,k,d^{\vee}]](../../_images/math/e081959b1f50aba12fd09c2d616bb9678e4358a7.png) code, where
code, where 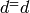 (if d is even) and
(if d is even) and 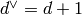 (if
(if 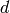 is odd).
is odd).
EXAMPLES:
sage: C = HammingCode(3,GF(4,'a'))
sage: C
Linear code of length 21, dimension 18 over Finite Field in a of size 2^2
sage: Cx = C.extended_code()
sage: Cx
Linear code of length 22, dimension 18 over Finite Field in a of size 2^2
If self is a linear code defined over  and
and 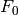 is a subfield
with Galois group
is a subfield
with Galois group 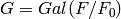 then this returns the
then this returns the  -module
-module
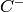 containing
containing  .
.
EXAMPLES:
sage: C = HammingCode(3,GF(4,'a'))
sage: Cc = C.galois_closure(GF(2))
sage: C; Cc
Linear code of length 21, dimension 18 over Finite Field in a of size 2^2
Linear code of length 21, dimension 20 over Finite Field in a of size 2^2
sage: c = C.basis()[1]
sage: V = VectorSpace(GF(4,'a'),21)
sage: c2 = V([x^2 for x in c.list()])
sage: c2 in C
False
sage: c2 in Cc
True
Return a generator matrix of this code.
EXAMPLES:
sage: C1 = HammingCode(3,GF(2))
sage: C1.gen_mat()
[1 0 0 1 0 1 0]
[0 1 0 1 0 1 1]
[0 0 1 1 0 0 1]
[0 0 0 0 1 1 1]
sage: C2 = HammingCode(2,GF(4,"a"))
sage: C2.gen_mat()
[ 1 0 0 1 1]
[ 0 1 0 1 a + 1]
[ 0 0 1 1 a]
Return a systematic generator matrix of the code.
A generator matrix of a code is called systematic if it contains a set of columns forming an identity matrix.
EXAMPLES:
sage: G = matrix(GF(3),2,[1,-1,1,-1,1,1])
sage: code = LinearCode(G)
sage: code.gen_mat()
[1 2 1]
[2 1 1]
sage: code.gen_mat_systematic()
[1 2 0]
[0 0 1]
Returns the generators of this code as a list of vectors.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.gens()
[(1, 0, 0, 1, 0, 1, 0), (0, 1, 0, 1, 0, 1, 1), (0, 0, 1, 1, 0, 0, 1), (0, 0, 0, 0, 1, 1, 1)]
Returns the “Duursma genus” of the code, 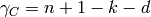 .
.
EXAMPLES:
sage: C1 = HammingCode(3,GF(2)); C1
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C1.genus()
1
sage: C2 = HammingCode(2,GF(4,"a")); C2
Linear code of length 5, dimension 3 over Finite Field in a of size 2^2
sage: C2.genus()
0
Since all Hamming codes have minimum distance 3, these computations
agree with the definition, 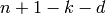 .
.
Return an information set of the code.
A set of column positions of a generator matrix of a code is called an information set if the corresponding columns form a square matrix of full rank.
OUTPUT:
EXAMPLES:
sage: G = matrix(GF(3),2,[1,-1,0,-1,1,1])
sage: code = LinearCode(G)
sage: code.gen_mat_systematic()
[1 2 0]
[0 0 1]
sage: code.information_set()
[0, 2]
Checks if self is equal to its Galois closure.
EXAMPLES:
sage: C = HammingCode(3,GF(4,"a"))
sage: C.is_galois_closed()
False
Returns 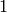 if
if 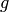 is an element of
is an element of 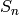 (
( = length of self) and
if
= length of self) and
if 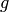 is an automorphism of self.
is an automorphism of self.
EXAMPLES:
sage: C = HammingCode(3,GF(3))
sage: g = SymmetricGroup(13).random_element()
sage: C.is_permutation_automorphism(g)
0
sage: MS = MatrixSpace(GF(2),4,8)
sage: G = MS([[1,0,0,0,1,1,1,0],[0,1,1,1,0,0,0,0],[0,0,0,0,0,0,0,1],[0,0,0,0,0,1,0,0]])
sage: C = LinearCode(G)
sage: S8 = SymmetricGroup(8)
sage: g = S8("(2,3)")
sage: C.is_permutation_automorphism(g)
1
sage: g = S8("(1,2,3,4)")
sage: C.is_permutation_automorphism(g)
0
Returns True if self and other are permutation equivalent codes and False otherwise.
The method="verbose" option also returns a permutation (if True) sending self to other.
Uses Robert Miller’s double coset partition refinement work.
EXAMPLES:
sage: P.<x> = PolynomialRing(GF(2),"x")
sage: g = x^3+x+1
sage: C1 = CyclicCodeFromGeneratingPolynomial(7,g); C1
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C2 = HammingCode(3,GF(2)); C2
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C1.is_permutation_equivalent(C2)
True
sage: C1.is_permutation_equivalent(C2,method="verbose")
(True, (4,6,5,7))
sage: C1 = RandomLinearCode(10,5,GF(2))
sage: C2 = RandomLinearCode(10,5,GF(3))
sage: C1.is_permutation_equivalent(C2)
False
Returns True if the code is self-dual (in the usual Hamming inner product) and False otherwise.
EXAMPLES:
sage: C = ExtendedBinaryGolayCode()
sage: C.is_self_dual()
True
sage: C = HammingCode(3,GF(2))
sage: C.is_self_dual()
False
Returns True if this code is self-orthogonal and False otherwise.
A code is self-orthogonal if it is a subcode of its dual.
EXAMPLES:
sage: C = ExtendedBinaryGolayCode()
sage: C.is_self_orthogonal()
True
sage: C = HammingCode(3,GF(2))
sage: C.is_self_orthogonal()
False
sage: C = QuasiQuadraticResidueCode(11) # requires optional GAP package Guava
sage: C.is_self_orthogonal() # requires optional GAP package Guava
True
Returns True if self is a subcode of other.
EXAMPLES:
sage: C1 = HammingCode(3,GF(2))
sage: G1 = C1.gen_mat()
sage: G2 = G1.matrix_from_rows([0,1,2])
sage: C2 = LinearCode(G2)
sage: C2.is_subcode(C1)
True
sage: C1.is_subcode(C2)
False
sage: C3 = C1.extended_code()
sage: C1.is_subcode(C3)
False
sage: C4 = C1.punctured([1])
sage: C4.is_subcode(C1)
False
sage: C5 = C1.shortened([1])
sage: C5.is_subcode(C1)
False
sage: C1 = HammingCode(3,GF(9,"z"))
sage: G1 = C1.gen_mat()
sage: G2 = G1.matrix_from_rows([0,1,2])
sage: C2 = LinearCode(G2)
sage: C2.is_subcode(C1)
True
Returns the length of this code.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.length()
7
Return a list of all elements of this linear code.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: Clist = C.list()
sage: Clist[5]; Clist[5] in C
(1, 0, 1, 0, 0, 1, 1)
True
Returns the minimum distance of this linear code.
By default, this uses a GAP kernel function (in C and not part of
Guava) written by Steve Linton. If method="guava" is set and
 is 2 or 3 then this uses a very fast program written in C written
by CJ Tjhal. (This is much faster, except in some small examples.)
is 2 or 3 then this uses a very fast program written in C written
by CJ Tjhal. (This is much faster, except in some small examples.)
Raises a ValueError in case there is no non-zero vector in this linear code.
INPUT:
OUTPUT:
EXAMPLES:
sage: MS = MatrixSpace(GF(3),4,7)
sage: G = MS([[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C.minimum_distance()
3
sage: C.minimum_distance(method="guava") # requires optional GAP package Guava
3
sage: C = HammingCode(2,GF(4,"a")); C
Linear code of length 5, dimension 3 over Finite Field in a of size 2^2
sage: C.minimum_distance()
3
This shows that trac ticket #6486 has been resolved:
sage: G = matrix(GF(2),[[0,0,0]])
sage: C = LinearCode(G)
sage: C.minimum_distance()
...
ValueError: this linear code contains no non-zero vector
Prints the GAP record of the Meataxe composition factors module in Meataxe notation. This uses GAP but not Guava.
EXAMPLES:
sage: MS = MatrixSpace(GF(2),4,8)
sage: G = MS([[1,0,0,0,1,1,1,0],[0,1,1,1,0,0,0,0],[0,0,0,0,0,0,0,1],[0,0,0,0,0,1,0,0]])
sage: C = LinearCode(G)
sage: gp = C.automorphism_group_binary_code()
Now type “C.module_composition_factors(gp)” to get the record printed.
If  is an
is an ![[n,k,d]](../../_images/math/cc42e8e038862e16c362efb9b3d2b9e56b81091e.png) code over
code over  , this function computes the
subgroup
, this function computes the
subgroup 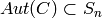 of all permutation automorphisms of
of all permutation automorphisms of  .
The binary case always uses the (default) partition refinement method
of Robert Miller.
.
The binary case always uses the (default) partition refinement method
of Robert Miller.
INPUT:
OUTPUT:
EXAMPLES:
sage: MS = MatrixSpace(GF(2),4,8)
sage: G = MS([[1,0,0,0,1,1,1,0],[0,1,1,1,0,0,0,0],[0,0,0,0,0,0,0,1],[0,0,0,0,0,1,0,0]])
sage: C = LinearCode(G)
sage: C
Linear code of length 8, dimension 4 over Finite Field of size 2
sage: G = C.permutation_automorphism_group()
sage: G.order()
144
A less easy example involves showing that the permutation
automorphism group of the extended ternary Golay code is the
Mathieu group 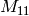 .
.
sage: C = ExtendedTernaryGolayCode()
sage: M11 = MathieuGroup(11)
sage: M11.order()
7920
sage: G = C.permutation_automorphism_group() # this should take < 5 seconds
sage: G.is_isomorphic(M11) # this should take < 5 seconds
True
In the binary case, uses sage.coding.binary_code:
sage: C = ExtendedBinaryGolayCode()
sage: G = C.permutation_automorphism_group()
sage: G.order()
244823040
In the non-binary case:
sage: C = HammingCode(2,GF(3)); C
Linear code of length 4, dimension 2 over Finite Field of size 3
sage: C.permutation_automorphism_group(method="partition")
Permutation Group with generators [(1,2,3)]
sage: C = HammingCode(2,GF(4,"z")); C
Linear code of length 5, dimension 3 over Finite Field in z of size 2^2
sage: C.permutation_automorphism_group(method="partition")
Permutation Group with generators [(1,2)(3,4), (1,3)(2,4)]
sage: C.permutation_automorphism_group(method="gap") # requires optional GAP package Guava
Permutation Group with generators [(1,2)(3,4), (1,3)(2,4)]
sage: C = TernaryGolayCode()
sage: C.permutation_automorphism_group(method="gap") # requires optional GAP package Guava
Permutation Group with generators [(3,4)(5,7)(6,9)(8,11), (3,5,8)(4,11,7)(6,9,10), (2,3)(4,6)(5,8)(7,10), (1,2)(4,11)(5,8)(9,10)]
However, the option method="gap+verbose", will print out:
Minimum distance: 5 Weight distribution: [1, 0, 0, 0, 0, 132, 132,
0, 330, 110, 0, 24]
Using the 132 codewords of weight 5 Supergroup size: 39916800
in addition to the output of C.permutation_automorphism_group(method="gap").
Returns the permuted code, which is equivalent to self via the column permutation p.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: G = C.automorphism_group_binary_code(); G
Permutation Group with generators [(3,4)(5,6), (3,5)(4,6), (2,3)(5,7), (1,2)(5,6)]
sage: g = G("(2,3)(5,7)")
sage: Cg = C.permuted_code(g)
sage: Cg
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C == Cg
True
Returns the code punctured at the positions 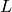 ,
,
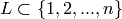 . If this code
. If this code  is of length
is of length  in
GF(q) then the code
in
GF(q) then the code 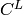 obtained from
obtained from  by puncturing at the
positions in
by puncturing at the
positions in 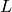 is the code of length
is the code of length 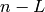 consisting of codewords
of
consisting of codewords
of  which have their
which have their 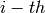 coordinate deleted if
coordinate deleted if 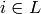 and
left alone if
and
left alone if 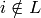 :
:
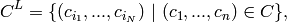
where 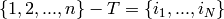 . In particular, if
. In particular, if 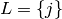 then
then 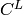 is simply the code obtainen from
is simply the code obtainen from  by deleting the
by deleting the 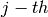 coordinate of each codeword. The code
coordinate of each codeword. The code 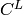 is called the punctured
code at
is called the punctured
code at 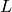 . The dimension of
. The dimension of 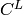 can decrease if
can decrease if 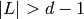 .
.
INPUT:
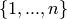 , where
, where  is the length of self
is the length of selfOUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.punctured([1,2])
Linear code of length 5, dimension 4 over Finite Field of size 2
Returns a random codeword.
OUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(4,'a'))
sage: Cc = C.galois_closure(GF(2))
sage: c = C.gen_mat()[1]
sage: V = VectorSpace(GF(4,'a'),21)
sage: c2 = V([x^2 for x in c.list()])
sage: c2 in C
False
sage: c2 in Cc
True
If C is a linear [n,k,d] code then this function returns a
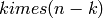 matrix A such that G = (I,A) generates a code (in
standard form) equivalent to C. If C is already in standard form and
G = (I,A) is its generator matrix then this function simply returns
that A.
matrix A such that G = (I,A) generates a code (in
standard form) equivalent to C. If C is already in standard form and
G = (I,A) is its generator matrix then this function simply returns
that A.
OUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.gen_mat()
[1 0 0 1 0 1 0]
[0 1 0 1 0 1 1]
[0 0 1 1 0 0 1]
[0 0 0 0 1 1 1]
sage: C.redundancy_matrix()
[1 1 0]
[1 1 1]
[1 0 1]
[0 1 1]
sage: C.standard_form()[0].gen_mat()
[1 0 0 0 1 1 0]
[0 1 0 0 1 1 1]
[0 0 1 0 1 0 1]
[0 0 0 1 0 1 1]
sage: C = HammingCode(2,GF(3))
sage: C.gen_mat()
[1 0 2 2]
[0 1 2 1]
sage: C.redundancy_matrix()
[2 2]
[2 1]
Returns the Duursma data  and
and 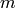 of this formally s.d. code
of this formally s.d. code  and the type number
and the type number  in (1,2,3,4). Does not check if this code
is actually sd.
in (1,2,3,4). Does not check if this code
is actually sd.
INPUT:
OUTPUT:
REFERENCES:
| [D] | (1, 2, 3) I. Duursma, “Extremal weight enumerators and ultraspherical polynomials” |
INPUT:
 is actually an sd code
is actually an sd code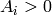 iff
iff
 is divisible by
is divisible by 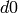
OUTPUT:
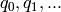 of
of 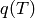 as in Duursma [D]
as in Duursma [D]REFERENCES:
Returns the Duursma zeta function of a self-dual code using the construction in [D].
INPUT:
OUTPUT:
EXAMPLES:
sage: C1 = HammingCode(3,GF(2))
sage: C2 = C1.extended_code(); C2
Linear code of length 8, dimension 4 over Finite Field of size 2
sage: C2.is_self_dual()
True
sage: C2.sd_zeta_polynomial()
2/5*T^2 + 2/5*T + 1/5
sage: C2.zeta_polynomial()
2/5*T^2 + 2/5*T + 1/5
sage: P = C2.sd_zeta_polynomial(); P(1)
1
sage: F.<z> = GF(4,"z")
sage: MS = MatrixSpace(F, 3, 6)
sage: G = MS([[1,0,0,1,z,z],[0,1,0,z,1,z],[0,0,1,z,z,1]])
sage: C = LinearCode(G) # the "hexacode"
sage: C.sd_zeta_polynomial(4)
1
It is a general fact about Duursma zeta polynomials that 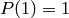 .
.
REFERENCES:
Returns the code shortened at the positions L, where
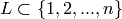 .
.
Consider the subcode 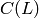 consisting of all codewords
consisting of all codewords 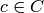 which
satisfy
which
satisfy 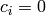 for all
for all 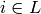 . The punctured code
. The punctured code 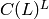 is
called the shortened code on
is
called the shortened code on 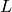 and is denoted
and is denoted 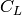 . The code
constructed is actually only isomorphic to the shortened code defined
in this way.
. The code
constructed is actually only isomorphic to the shortened code defined
in this way.
By Theorem 1.5.7 in [HP], 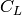 is
is 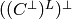 . This is used
in the construction below.
. This is used
in the construction below.
INPUT:
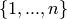 , where
, where  is the length of this code
is the length of this codeOUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.shortened([1,2])
Linear code of length 5, dimension 2 over Finite Field of size 2
Returns the spectrum of self as a list.
The default method uses a GAP kernel function (in C) written by Steve Linton.
INPUT:
The optional method ("leon") may create a stack smashing error and a traceback but should return the correct answer. It appears to run much faster than the GAP method in some small examples and much slower than the GAP method in other larger examples.
EXAMPLES:
sage: MS = MatrixSpace(GF(2),4,7)
sage: G = MS([[1,1,1,0,0,0,0],[1,0,0,1,1,0,0],[0,1,0,1,0,1,0],[1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C.spectrum()
[1, 0, 0, 7, 7, 0, 0, 1]
sage: F.<z> = GF(2^2,"z")
sage: C = HammingCode(2, F); C
Linear code of length 5, dimension 3 over Finite Field in z of size 2^2
sage: C.spectrum()
[1, 0, 0, 30, 15, 18]
sage: C = HammingCode(3,GF(2)); C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C.spectrum(method="leon") # requires optional GAP package Guava
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C.spectrum(method="gap")
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C.spectrum(method="binary")
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C = HammingCode(3,GF(3)); C
Linear code of length 13, dimension 10 over Finite Field of size 3
sage: C.spectrum() == C.spectrum(method="leon") # requires optional GAP package Guava
True
sage: C = HammingCode(2,GF(5)); C
Linear code of length 6, dimension 4 over Finite Field of size 5
sage: C.spectrum() == C.spectrum(method="leon") # requires optional GAP package Guava
True
sage: C = HammingCode(2,GF(7)); C
Linear code of length 8, dimension 6 over Finite Field of size 7
sage: C.spectrum() == C.spectrum(method="leon") # requires optional GAP package Guava
True
Returns the standard form of this linear code.
An ![[n,k]](../../_images/math/8f1604bbabe0f4f7338f67a11ec78e8f0519909d.png) linear code with generator matrix
linear code with generator matrix  in standard form is
the row-reduced echelon form of
in standard form is
the row-reduced echelon form of  is
is 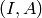 , where
, where 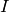 denotes the
denotes the
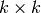 identity matrix and
identity matrix and 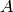 is a
is a 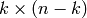 block. This
method returns a pair
block. This
method returns a pair 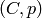 where
where  is a code permutation
equivalent to self and
is a code permutation
equivalent to self and  in
in 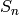 , with
, with  the length of
the length of  ,
is the permutation sending self to
,
is the permutation sending self to  . This does not call GAP.
. This does not call GAP.
Thanks to Frank Luebeck for (the GAP version of) this code.
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.gen_mat()
[1 0 0 1 0 1 0]
[0 1 0 1 0 1 1]
[0 0 1 1 0 0 1]
[0 0 0 0 1 1 1]
sage: Cs,p = C.standard_form()
sage: p
(4,5)
sage: Cs
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: Cs.gen_mat()
[1 0 0 0 1 1 0]
[0 1 0 0 1 1 1]
[0 0 1 0 1 0 1]
[0 0 0 1 0 1 1]
sage: MS = MatrixSpace(GF(3),3,7)
sage: G = MS([[1,0,0,0,1,1,0],[0,1,0,1,0,1,0],[0,0,0,0,0,0,1]])
sage: C = LinearCode(G)
sage: G; C.standard_form()[0].gen_mat()
[1 0 0 0 1 1 0]
[0 1 0 1 0 1 0]
[0 0 0 0 0 0 1]
[1 0 0 0 1 1 0]
[0 1 0 1 0 1 0]
[0 0 1 0 0 0 0]
sage: C.standard_form()[1]
(3,7)
Returns the set of indices 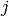 where
where 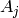 is nonzero, where
spectrum(self) =
is nonzero, where
spectrum(self) = ![[A_0,A_1,...,A_n]](../../_images/math/c12b3196288f25082bebb5a19365c519023cd986.png) .
.
OUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.spectrum()
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C.support()
[0, 3, 4, 7]
Returns the spectrum of self as a list.
The default method uses a GAP kernel function (in C) written by Steve Linton.
INPUT:
The optional method ("leon") may create a stack smashing error and a traceback but should return the correct answer. It appears to run much faster than the GAP method in some small examples and much slower than the GAP method in other larger examples.
EXAMPLES:
sage: MS = MatrixSpace(GF(2),4,7)
sage: G = MS([[1,1,1,0,0,0,0],[1,0,0,1,1,0,0],[0,1,0,1,0,1,0],[1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
sage: C.spectrum()
[1, 0, 0, 7, 7, 0, 0, 1]
sage: F.<z> = GF(2^2,"z")
sage: C = HammingCode(2, F); C
Linear code of length 5, dimension 3 over Finite Field in z of size 2^2
sage: C.spectrum()
[1, 0, 0, 30, 15, 18]
sage: C = HammingCode(3,GF(2)); C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: C.spectrum(method="leon") # requires optional GAP package Guava
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C.spectrum(method="gap")
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C.spectrum(method="binary")
[1, 0, 0, 7, 7, 0, 0, 1]
sage: C = HammingCode(3,GF(3)); C
Linear code of length 13, dimension 10 over Finite Field of size 3
sage: C.spectrum() == C.spectrum(method="leon") # requires optional GAP package Guava
True
sage: C = HammingCode(2,GF(5)); C
Linear code of length 6, dimension 4 over Finite Field of size 5
sage: C.spectrum() == C.spectrum(method="leon") # requires optional GAP package Guava
True
sage: C = HammingCode(2,GF(7)); C
Linear code of length 8, dimension 6 over Finite Field of size 7
sage: C.spectrum() == C.spectrum(method="leon") # requires optional GAP package Guava
True
Returns the weight enumerator of the code.
INPUT:
OUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.weight_enumerator()
x^7 + 7*x^4*y^3 + 7*x^3*y^4 + y^7
sage: C.weight_enumerator(names="st")
s^7 + 7*s^4*t^3 + 7*s^3*t^4 + t^7
Returns the Duursma zeta function of the code.
INPUT:
OUTPUT:
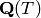
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.zeta_function()
(2/5*T^2 + 2/5*T + 1/5)/(2*T^2 - 3*T + 1)
Returns the Duursma zeta polynomial of this code.
Assumes that the minimum distances of this code and its dual are greater than 1. Prints a warning to stdout otherwise.
INPUT:
OUTPUT:
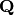
EXAMPLES:
sage: C = HammingCode(3,GF(2))
sage: C.zeta_polynomial()
2/5*T^2 + 2/5*T + 1/5
sage: C = best_known_linear_code(6,3,GF(2)) # requires optional GAP package Guava
sage: C.minimum_distance() # requires optional GAP package Guava
3
sage: C.zeta_polynomial() # requires optional GAP package Guava
2/5*T^2 + 2/5*T + 1/5
sage: C = HammingCode(4,GF(2))
sage: C.zeta_polynomial()
16/429*T^6 + 16/143*T^5 + 80/429*T^4 + 32/143*T^3 + 30/143*T^2 + 2/13*T + 1/13
sage: F.<z> = GF(4,"z")
sage: MS = MatrixSpace(F, 3, 6)
sage: G = MS([[1,0,0,1,z,z],[0,1,0,z,1,z],[0,0,1,z,z,1]])
sage: C = LinearCode(G) # the "hexacode"
sage: C.zeta_polynomial()
1
REFERENCES:
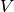 of
of 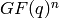 into a
into a  .
.Returns the best known (as of 11 May 2006) linear code of length n, dimension k over field F. The function uses the tables described in bounds_minimum_distance to construct this code.
This does not require an internet connection.
EXAMPLES:
sage: best_known_linear_code(10,5,GF(2)) # long time and requires optional GAP package Guava
Linear code of length 10, dimension 5 over Finite Field of size 2
sage: gap.eval("C:=BestKnownLinearCode(10,5,GF(2))") # long time and requires optional GAP package Guava
'a linear [10,5,4]2..4 shortened code'
This means that best possible binary linear code of length 10 and dimension 5 is a code with minimum distance 4 and covering radius somewhere between 2 and 4. Use minimum_distance_why(10,5,GF(2)) or print bounds_minimum_distance(10,5,GF(2)) for further details.
Explains the construction of the best known linear code over GF(q) with length n and dimension k, courtesy of the www page http://www.codetables.de/.
INPUT:
OUTPUT:
EXAMPLES:
sage: L = best_known_linear_code_www(72, 36, GF(2)) # requires internet, optional
sage: print L # requires internet, optional
Construction of a linear code
[72,36,15] over GF(2):
[1]: [73, 36, 16] Cyclic Linear Code over GF(2)
CyclicCode of length 73 with generating polynomial x^37 + x^36 + x^34 +
x^33 + x^32 + x^27 + x^25 + x^24 + x^22 + x^21 + x^19 + x^18 + x^15 + x^11 +
x^10 + x^8 + x^7 + x^5 + x^3 + 1
[2]: [72, 36, 15] Linear Code over GF(2)
Puncturing of [1] at 1
last modified: 2002-03-20
This function raises an IOError if an error occurs downloading data or parsing it. It raises a ValueError if the q input is invalid.
AUTHORS:
Calculates a lower and upper bound for the minimum distance of an optimal linear code with word length n and dimension k over the field F.
The function returns a record with the two bounds and an explanation for each bound. The function Display can be used to show the explanations.
The values for the lower and upper bound are obtained from a table
constructed by Cen Tjhai for GUAVA, derived from the table of
Brouwer. (See http://www.win.tue.nl/ aeb/voorlincod.html or use the
Sage function minimum_distance_why for the most recent data.)
These tables contain lower and upper bounds for 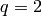 (when n <= 257),
(when n <= 257),
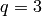 (when n <= 243),
(when n <= 243), 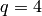 (n <= 256). (Current as of
11 May 2006.) For codes over other fields and for larger word lengths,
trivial bounds are used.
(n <= 256). (Current as of
11 May 2006.) For codes over other fields and for larger word lengths,
trivial bounds are used.
This does not require an internet connection. The format of the output is a little non-intuitive. Try bounds_minimum_distance(10,5,GF(2)) for an example.
This function requires optional GAP package (Guava).
Writes a file in Sage’s temp directory representing the code C, returning the absolute path to the file. This is the Sage translation of the GuavaToLeon command in Guava’s codefun.gi file.
INPUT:
OUTPUT:
EXAMPLES:
sage: C = HammingCode(3,GF(2)); C
Linear code of length 7, dimension 4 over Finite Field of size 2
sage: file_loc = sage.coding.linear_code.code2leon(C)
sage: f = open(file_loc); print f.read()
LIBRARY code;
code=seq(2,4,7,seq(
1,0,0,1,0,1,0,
0,1,0,1,0,1,1,
0,0,1,1,0,0,1,
0,0,0,0,1,1,1
));
FINISH;
sage: f.close()
Returns the Hamming weight of the vector v, which is the number of non-zero entries.
INPUT:
OUTPUT:
EXAMPLES:
sage: hamming_weight(vector(GF(2),[0,0,1]))
1
sage: hamming_weight(vector(GF(2),[0,0,0]))
0
Returns a minimum weight vector of the code generated by Gmat.
Uses C programs written by Steve Linton in the kernel of GAP, so is fairly fast. The option method="guava" requires Guava. The default method requires GAP but not Guava.
INPUT:
OUTPUT:
REMARKS:
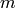 such that
such that 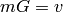 , and the (minimum) distance, as
a triple. however, this output is not implemented.
, and the (minimum) distance, as
a triple. however, this output is not implemented.EXAMPLES:
sage: Gstr = "Z(2)*[[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]]"
sage: sage.coding.linear_code.min_wt_vec_gap(Gstr,7,4,GF(2))
(0, 1, 0, 1, 0, 1, 0)
This output is different but still a minimum weight vector:
sage: sage.coding.linear_code.min_wt_vec_gap(Gstr,7,4,GF(2),method="guava") # requires optional GAP package Guava
(0, 0, 1, 0, 1, 1, 0)
Here Gstr is a generator matrix of the Hamming [7,4,3] binary code.
AUTHORS:
Returns a Python iterator which generates a complete set of representatives of all permutation equivalence classes of self-orthogonal binary linear codes of length in [1..n] and dimension in [1..k].
INPUT:
EXAMPLES:
Generate all self-orthogonal codes of length up to 7 and dimension up to 3:
sage: for B in self_orthogonal_binary_codes(7,3):
... print B
...
Linear code of length 2, dimension 1 over Finite Field of size 2
Linear code of length 4, dimension 2 over Finite Field of size 2
Linear code of length 6, dimension 3 over Finite Field of size 2
Linear code of length 4, dimension 1 over Finite Field of size 2
Linear code of length 6, dimension 2 over Finite Field of size 2
Linear code of length 6, dimension 2 over Finite Field of size 2
Linear code of length 7, dimension 3 over Finite Field of size 2
Linear code of length 6, dimension 1 over Finite Field of size 2
Generate all doubly-even codes of length up to 7 and dimension up to 3:
sage: for B in self_orthogonal_binary_codes(7,3,4):
... print B; print B.gen_mat()
...
Linear code of length 4, dimension 1 over Finite Field of size 2
[1 1 1 1]
Linear code of length 6, dimension 2 over Finite Field of size 2
[1 1 1 1 0 0]
[0 1 0 1 1 1]
Linear code of length 7, dimension 3 over Finite Field of size 2
[1 0 1 1 0 1 0]
[0 1 0 1 1 1 0]
[0 0 1 0 1 1 1]
Generate all doubly-even codes of length up to 7 and dimension up to 2:
sage: for B in self_orthogonal_binary_codes(7,2,4):
... print B; print B.gen_mat()
Linear code of length 4, dimension 1 over Finite Field of size 2
[1 1 1 1]
Linear code of length 6, dimension 2 over Finite Field of size 2
[1 1 1 1 0 0]
[0 1 0 1 1 1]
Generate all self-orthogonal codes of length equal to 8 and dimension equal to 4:
sage: for B in self_orthogonal_binary_codes(8, 4, equal=True):
... print B; print B.gen_mat()
Linear code of length 8, dimension 4 over Finite Field of size 2
[1 0 0 1 0 0 0 0]
[0 1 0 0 1 0 0 0]
[0 0 1 0 0 1 0 0]
[0 0 0 0 0 0 1 1]
Linear code of length 8, dimension 4 over Finite Field of size 2
[1 0 0 1 1 0 1 0]
[0 1 0 1 1 1 0 0]
[0 0 1 0 1 1 1 0]
[0 0 0 1 0 1 1 1]
Since all the codes will be self-orthogonal, b must be divisible by 2:
sage: list(self_orthogonal_binary_codes(8, 4, 1, equal=True))
...
ValueError: b (1) must be a positive even integer.
INPUT:
OUTPUT:
EXAMPLES:
sage: Gstr = 'Z(2)*[[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]]'
sage: F = GF(2)
sage: sage.coding.linear_code.wtdist_gap(Gstr, 7, F)
[1, 0, 0, 7, 7, 0, 0, 1]
Here Gstr is a generator matrix of the Hamming [7,4,3] binary code.
ALGORITHM:
Uses C programs written by Steve Linton in the kernel of GAP, so is fairly fast.
AUTHORS: