Groups

class sage.categories.groups.Groups(s=None)

Bases: sage.categories.category.Category

The category of (multiplicative) groups, i.e. monoids with inverses.

EXAMPLES:

sage: Groups()
Category of groups
sage: Groups().super_categories()
[Category of monoids]

TESTS:

sage: TestSuite(Groups()).run()

class ElementMethods

class Groups.ParentMethods

cayley_table(names='letters', elements=None)

Returns the “multiplication” table of this multiplicative group, which is also known as the “Cayley table.”

Note

The order of the elements in the row and column headings is equal to the order given by the table’s column_keys() method. The association between the actual elements and the names/symbols used in the table can also be retrieved as a dictionary with the translation() method.

For groups, this routine should behave identically to the multiplication_table() method for magmas, which applies in greater generality.

INPUT:

• names - the type of names used, values are:
  • letters - lowercase ASCII letters are used for a base 26 representation of the elements’ positions in the list given by list(), padded to a common width with leading ‘a’s.
  • digits - base 10 representation of the elements’ positions in the list given by column_keys(), padded to a common width with leading zeros.
  • elements - the string representations of the elements themselves.
  • a list - a list of strings, where the length of the list equals the number of elements.
• elements - default = None. A list of elements of the set. This may be used to impose an alternate ordering on the elements, perhaps when this is used in the context of a particular structure. The default is to use whatever ordering is provided by the the group, which is reported by the column_keys() method. Or the elements can be a subset which is closed under the operation. In particular, this can be used when the base set is infinite.

OUTPUT: An object representing the multiplication table. This is an OperationTable object and even more documentation can be found there.

EXAMPLES:

Permutation groups, matrix groups and abelian groups can all compute their multiplication tables.

sage: G = DiCyclicGroup(3)
sage: T = G.cayley_table()
sage: T.column_keys()
((), (5,6,7), (5,7,6)...(1,4,2,3)(5,7))
sage: T
*  a b c d e f g h i j k l
+------------------------
a| a b c d e f g h i j k l
b| b c a e f d i g h l j k
c| c a b f d e h i g k l j
d| d e f a b c j k l g h i
e| e f d b c a l j k i g h
f| f d e c a b k l j h i g
g| g h i j k l d e f a b c
h| h i g k l j f d e c a b
i| i g h l j k e f d b c a
j| j k l g h i a b c d e f
k| k l j h i g c a b f d e
l| l j k i g h b c a e f d

sage: M=SL(2,2)
sage: M.cayley_table()
*  a b c d e f
 +------------
a| d c b a f e
b| e f a b c d
c| f e d c b a
d| a b c d e f
e| b a f e d c
f| c d e f a b

sage: A=AbelianGroup([2,3])
sage: A.cayley_table()
*  a b c d e f
+------------
a| a b c d e f
b| b c a e f d
c| c a b f d e
d| d e f a b c
e| e f d b c a
f| f d e c a b

Lowercase ASCII letters are the default symbols used for the table, but you can also specify the use of decimal digit strings, or provide your own strings (in the proper order if they have meaning). Also, if the elements themselves are not too complex, you can choose to just use the string representations of the elements themselves.

sage: C=CyclicPermutationGroup(11)
sage: C.cayley_table(names='digits')
 *  00 01 02 03 04 05 06 07 08 09 10
  +---------------------------------
00| 00 01 02 03 04 05 06 07 08 09 10
01| 01 02 03 04 05 06 07 08 09 10 00
02| 02 03 04 05 06 07 08 09 10 00 01
03| 03 04 05 06 07 08 09 10 00 01 02
04| 04 05 06 07 08 09 10 00 01 02 03
05| 05 06 07 08 09 10 00 01 02 03 04
06| 06 07 08 09 10 00 01 02 03 04 05
07| 07 08 09 10 00 01 02 03 04 05 06
08| 08 09 10 00 01 02 03 04 05 06 07
09| 09 10 00 01 02 03 04 05 06 07 08
10| 10 00 01 02 03 04 05 06 07 08 09

sage: G=QuaternionGroup()
sage: names=['1', 'I', '-1', '-I', 'J', '-K', '-J', 'K']
sage: G.cayley_table(names=names)
 *   1  I -1 -I  J -K -J  K
  +------------------------
 1|  1  I -1 -I  J -K -J  K
 I|  I -1 -I  1  K  J -K -J
-1| -1 -I  1  I -J  K  J -K
-I| -I  1  I -1 -K -J  K  J
 J|  J -K -J  K -1 -I  1  I
-K| -K -J  K  J  I -1 -I  1
-J| -J  K  J -K  1  I -1 -I
 K|  K  J -K -J -I  1  I -1

sage: A=AbelianGroup([2,2])
sage: A.cayley_table(names='elements')
    *      1    f1    f0 f0*f1
     +------------------------
    1|     1    f1    f0 f0*f1
   f1|    f1     1 f0*f1    f0
   f0|    f0 f0*f1     1    f1
f0*f1| f0*f1    f0    f1     1

The change_names() routine behaves similarly, but changes an existing table “in-place.”

sage: G=AlternatingGroup(3)
sage: T=G.cayley_table()
sage: T.change_names('digits')
sage: T
*  0 1 2
 +------
0| 0 1 2
1| 1 2 0
2| 2 0 1

For an infinite group, you can still work with finite sets of elements, provided the set is closed under multiplication. Elements will be coerced into the group as part of setting up the table.

sage: G=SL(2,ZZ)
sage: G
Special Linear Group of degree 2 over Integer Ring
sage: identity = matrix(ZZ, [[1,0], [0,1]])
sage: G.cayley_table(elements=[identity, -identity])
*  a b
 +----
a| a b
b| b a

The OperationTable class provides even greater flexibility, including changing the operation. Here is one such example, illustrating the computation of commutators. commutator is defined as a function of two variables, before being used to build the table. From this, the commutator subgroup seems obvious, and creating a Cayley table with just these three elements confirms that they form a closed subset in the group.

sage: from sage.matrix.operation_table import OperationTable
sage: G=DiCyclicGroup(3)
sage: commutator = lambda x, y: x*y*x^-1*y^-1
sage: T=OperationTable(G, commutator)
sage: T
.  a b c d e f g h i j k l
 +------------------------
a| a a a a a a a a a a a a
b| a a a a a a c c c c c c
c| a a a a a a b b b b b b
d| a a a a a a a a a a a a
e| a a a a a a c c c c c c
f| a a a a a a b b b b b b
g| a b c a b c a c b a c b
h| a b c a b c b a c b a c
i| a b c a b c c b a c b a
j| a b c a b c a c b a c b
k| a b c a b c b a c b a c
l| a b c a b c c b a c b a
sage: trans = T.translation()
sage: comm = [trans['a'], trans['b'],trans['c']]
sage: comm
[(), (5,6,7), (5,7,6)]
sage: P=G.cayley_table(elements=comm)
sage: P
*  a b c
 +------
a| a b c
b| b c a
c| c a b

TODO:

Arrange an ordering of elements into cosets of a normal subgroup close to size 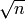. Then the quotient group structure is often apparent in the table. See comments on Trac #7555.

AUTHOR:

• Rob Beezer (2010-03-15)

group_generators()

Returns group generators for self.

This default implementation calls gens(), for backward compatibility.

EXAMPLES:

sage: A = AlternatingGroup(4)
sage: A.group_generators()
[(1,2,3), (2,3,4)]

Groups.super_categories(*args, **kwds)

EXAMPLES:

sage: Groups().super_categories()
[Category of monoids]