Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Category Theory »

Bases: sage.categories.category.Category
The category of crystals
See sage.combinat.crystals for an introduction to crystals.
EXAMPLES:
sage: C = Crystals()
sage: C
Category of crystals
sage: C.super_categories()
[Category of... enumerated sets]
sage: C.example()
Highest weight crystal of type A_3 of highest weight omega_1
Parents in this category should implement the following methods:
- either a method cartan_type or an attribute _cartan_type
- module_generators: a list (or container) of distinct elements which generate the crystal using
Furthermore, their elements should implement the following methods:
- x.e(i) (returning
)
- x.f(i) (returning
)
EXAMPLES:
sage: from sage.misc.abstract_method import abstract_methods_of_class
sage: abstract_methods_of_class(Crystals().element_class)
{'required': ['e', 'f'], 'optional': []}
TESTS:
sage: TestSuite(C).run()
sage: B = Crystals().example()
sage: TestSuite(B).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
Running the test suite of self.an_element()
running ._test_category() . . . pass
running ._test_eq() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
pass
running ._test_elements_eq() . . . pass
running ._test_enumerated_set_contains() . . . pass
running ._test_enumerated_set_iter_cardinality() . . . pass
running ._test_enumerated_set_iter_list() . . . pass
running ._test_eq() . . . pass
running ._test_fast_iter() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
running ._test_some_elements() . . . pass
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(0).Epsilon()
(0, 0, 0, 0, 0, 0)
sage: C(1).Epsilon()
(0, 0, 0, 0, 0, 0)
sage: C(2).Epsilon()
(1, 0, 0, 0, 0, 0)
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(0).Phi()
(0, 0, 0, 0, 0, 0)
sage: C(1).Phi()
(1, 0, 0, 0, 0, 0)
sage: C(2).Phi()
(1, 1, 0, 0, 0, 0)
Returns the cartan type associated to self
EXAMPLES:
sage: C = CrystalOfLetters(['A', 5])
sage: C(1).cartan_type()
['A', 5]
Returns the list of the elements one can obtain from
self by application of 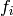 . If the option
“truncated” is set to True, then self is not included
in the list.
. If the option
“truncated” is set to True, then self is not included
in the list.
REFERENCES:
[L1995] Peter Littelmann, Crystal graphs and Young tableaux, J. Algebra 175 (1995), no. 1, 65–87.
[K1993] Masaki Kashiwara, The crystal base and Littelmann’s refined Demazure character formula, Duke Math. J. 71 (1993), no. 3, 839–858.
EXAMPLES:
sage: T = CrystalOfTableaux(['A',2], shape=[2,1])
sage: t=T(rows=[[1,2],[2]])
sage: t.demazure_operator(2)
[[[1, 2], [2]], [[1, 3], [2]], [[1, 3], [3]]]
sage: t.demazure_operator(2, truncated = True)
[[[1, 3], [2]], [[1, 3], [3]]]
sage: t.demazure_operator(1, truncated = True)
[]
sage: t.demazure_operator(1)
[[[1, 2], [2]]]
sage: K = KirillovReshetikhinCrystal(['A',2,1],2,1)
sage: t = K(rows=[[3],[2]])
sage: t.demazure_operator(0)
[[[2, 3]], [[1, 2]]]
Returns 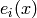 if it exists or None otherwise.
if it exists or None otherwise.
This method should be implemented by the element class of the crystal.
EXAMPLES:
sage: C = Crystals().example(5)
sage: x = C[2]; x
3
sage: x.e(1), x.e(2), x.e(3)
(None, 2, None)
Applies 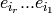 to self for
to self for ![list = [i_1, ..., i_r]](../../_images/math/5d6687bd93323bb39a79a49f7ff06c9e972e7dc8.png)
EXAMPLES:
sage: C = CrystalOfLetters(['A',3])
sage: b = C(3)
sage: b.e_string([2,1])
1
sage: b.e_string([1,2])
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(1).epsilon(1)
0
sage: C(2).epsilon(1)
1
Returns 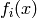 if it exists or None otherwise.
if it exists or None otherwise.
This method should be implemented by the element class of the crystal.
EXAMPLES:
sage: C = Crystals().example(5)
sage: x = C[1]; x
2
sage: x.f(1), x.f(2), x.f(3)
(None, 3, None)
Applies 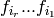 to self for
to self for ![list = [i_1, ..., i_r]](../../_images/math/5d6687bd93323bb39a79a49f7ff06c9e972e7dc8.png)
EXAMPLES:
sage: C = CrystalOfLetters(['A',3])
sage: b = C(1)
sage: b.f_string([1,2])
3
sage: b.f_string([2,1])
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(1).index_set()
[1, 2, 3, 4, 5]
Returns True if self is a highest weight.
Specifying the option index_set to be a subset  of the
index set of the underlying crystal, finds all highest
weight vectors for arrows in
of the
index set of the underlying crystal, finds all highest
weight vectors for arrows in  .
.
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(1).is_highest_weight()
True
sage: C(2).is_highest_weight()
False
sage: C(2).is_highest_weight(index_set = [2,3,4,5])
True
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(1).phi(1)
1
sage: C(2).phi(1)
0
Returns 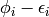 of self. There are sometimes
better implementations using the weight for this. It is used
for reflections along a string.
of self. There are sometimes
better implementations using the weight for this. It is used
for reflections along a string.
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(1).phi_minus_epsilon(1)
1
Returns the reflection of self along its  -string
-string
EXAMPLES:
sage: C = CrystalOfTableaux(['A',2], shape=[2,1])
sage: b=C(rows=[[1,1],[3]])
sage: b.s(1)
[[2, 2], [3]]
sage: b=C(rows=[[1,2],[3]])
sage: b.s(2)
[[1, 2], [3]]
sage: T=CrystalOfTableaux(['A',2],shape=[4])
sage: t=T(rows=[[1,2,2,2]])
sage: t.s(1)
[[1, 1, 1, 2]]
Returns the weight of this crystal element
EXAMPLES:
sage: C = CrystalOfLetters(['A',5])
sage: C(1).weight()
(1, 0, 0, 0, 0, 0)
Returns the fundamentals weights in the weight lattice realization for the root system associated the crystal
EXAMPLES:
sage: C = CrystalOfLetters(['A', 5])
sage: C.Lambda()
Finite family {1: (1, 0, 0, 0, 0, 0), 2: (1, 1, 0, 0, 0, 0), 3: (1, 1, 1, 0, 0, 0), 4: (1, 1, 1, 1, 0, 0), 5: (1, 1, 1, 1, 1, 0)}
Returns the Cartan type of the crystal
Constructs a morphism from the crystal self to another crystal.
The input 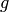 can either be a function of a (sub)set of elements of self to
element in another crystal or a dictionary between certain elements.
Usually one would map highest weight elements or crystal generators to each
other using g.
Specifying index_set gives the opportunity to define the morphism as
can either be a function of a (sub)set of elements of self to
element in another crystal or a dictionary between certain elements.
Usually one would map highest weight elements or crystal generators to each
other using g.
Specifying index_set gives the opportunity to define the morphism as  -crystals
where
-crystals
where 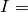 index_set. If index_set is not specified, the index set of self is used.
It is also possible to define twisted-morphisms by specifying an automorphism on the
nodes in te Dynkin diagram (or the index_set).
The option direction and direction_image indicate whether to use
index_set. If index_set is not specified, the index set of self is used.
It is also possible to define twisted-morphisms by specifying an automorphism on the
nodes in te Dynkin diagram (or the index_set).
The option direction and direction_image indicate whether to use 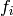 or
or 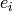 in
self or the image crystal to construct the morphism, depending on whether the direction
is set to ‘down’ or ‘up’.
It is also possible to set a similarity_factor. This should be a dictionary between
the elements in the index set and positive integers. The crystal operator
in
self or the image crystal to construct the morphism, depending on whether the direction
is set to ‘down’ or ‘up’.
It is also possible to set a similarity_factor. This should be a dictionary between
the elements in the index set and positive integers. The crystal operator 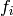 then gets
mapped to
then gets
mapped to 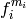 where
where 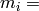 similarity_factor[i].
Setting similarity_factor_domain to a dictionary between the index set and positive integers
has the effect that
similarity_factor[i].
Setting similarity_factor_domain to a dictionary between the index set and positive integers
has the effect that 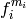 gets mapped to
gets mapped to 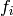 where
where 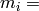 similarity_factor_domain[i].
Finally, it is possible to set the option
similarity_factor_domain[i].
Finally, it is possible to set the option 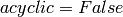 . This calculates an isomorphism
for cyclic crystals (for example finite affine crystals). In this case the input function
. This calculates an isomorphism
for cyclic crystals (for example finite affine crystals). In this case the input function 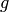 is supposed to be given as a dictionary.
is supposed to be given as a dictionary.
EXAMPLES:
sage: C2 = CrystalOfLetters(['A',2])
sage: C3 = CrystalOfLetters(['A',3])
sage: g = {C2.module_generators[0] : C3.module_generators[0]}
sage: g_full = C2.crystal_morphism(g)
sage: g_full(C2(1))
1
sage: g_full(C2(2))
2
sage: g = {C2(1) : C2(3)}
sage: g_full = C2.crystal_morphism(g, automorphism = lambda i : 3-i, direction_image = 'up')
sage: [g_full(b) for b in C2]
[3, 2, 1]
sage: T = CrystalOfTableaux(['A',2], shape = [2])
sage: g = {C2(1) : T(rows=[[1,1]])}
sage: g_full = C2.crystal_morphism(g, similarity_factor = {1:2, 2:2})
sage: [g_full(b) for b in C2]
[[[1, 1]], [[2, 2]], [[3, 3]]]
sage: g = {T(rows=[[1,1]]) : C2(1)}
sage: g_full = T.crystal_morphism(g, similarity_factor_domain = {1:2, 2:2})
sage: g_full(T(rows=[[2,2]]))
2
sage: B1=KirillovReshetikhinCrystal(['A',2,1],1,1)
sage: B2=KirillovReshetikhinCrystal(['A',2,1],1,2)
sage: T=TensorProductOfCrystals(B1,B2)
sage: T1=TensorProductOfCrystals(B2,B1)
sage: La = T.weight_lattice_realization().fundamental_weights()
sage: t = [b for b in T if b.weight() == -3*La[0] + 3*La[1]][0]
sage: t1 = [b for b in T1 if b.weight() == -3*La[0] + 3*La[1]][0]
sage: g={t:t1}
sage: f=T.crystal_morphism(g,acyclic = False)
sage: [[b,f(b)] for b in T]
[[[[[1]], [[1, 1]]], [[[1, 1]], [[1]]]],
[[[[1]], [[1, 2]]], [[[1, 1]], [[2]]]],
[[[[1]], [[2, 2]]], [[[1, 2]], [[2]]]],
[[[[1]], [[1, 3]]], [[[1, 1]], [[3]]]],
[[[[1]], [[2, 3]]], [[[1, 2]], [[3]]]],
[[[[1]], [[3, 3]]], [[[1, 3]], [[3]]]],
[[[[2]], [[1, 1]]], [[[1, 2]], [[1]]]],
[[[[2]], [[1, 2]]], [[[2, 2]], [[1]]]],
[[[[2]], [[2, 2]]], [[[2, 2]], [[2]]]],
[[[[2]], [[1, 3]]], [[[2, 3]], [[1]]]],
[[[[2]], [[2, 3]]], [[[2, 2]], [[3]]]],
[[[[2]], [[3, 3]]], [[[2, 3]], [[3]]]],
[[[[3]], [[1, 1]]], [[[1, 3]], [[1]]]],
[[[[3]], [[1, 2]]], [[[1, 3]], [[2]]]],
[[[[3]], [[2, 2]]], [[[2, 3]], [[2]]]],
[[[[3]], [[1, 3]]], [[[3, 3]], [[1]]]],
[[[[3]], [[2, 3]]], [[[3, 3]], [[2]]]],
[[[[3]], [[3, 3]]], [[[3, 3]], [[3]]]]]
Returns the DiGraph associated to self.
EXAMPLES:
sage: C = Crystals().example(5)
sage: C.digraph()
Digraph on 6 vertices
TODO: add more tests
Returns a dot_tex string representation of self.
EXAMPLES:
sage: C = CrystalOfLetters(['A',2])
sage: C.dot_tex()
'digraph G { \n node [ shape=plaintext ];\n N_0 [ label = " ", texlbl = "$1$" ];\n N_1 [ label = " ", texlbl = "$2$" ];\n N_2 [ label = " ", texlbl = "$3$" ];\n N_0 -> N_1 [ label = " ", texlbl = "1" ];\n N_1 -> N_2 [ label = " ", texlbl = "2" ];\n}'
Returns the index set of the Dynkin diagram underlying the crystal
Returns the crystal graph as a latex string. This can be exported to a file with self.latex_file(‘filename’).
See Graph.layout_graphviz() for further documentation on which packages are required.
EXAMPLES:
sage: C = CrystalOfLetters(['A', 5])
sage: C.latex() #optional requires dot2tex
...
sage: view(C, pdflatex = True, tightpage = True) # optional
Exports a file, suitable for pdflatex, to ‘filename’. This requires a proper installation of dot2tex in sage-python. For more information see the documentation for self.latex().
EXAMPLES:
sage: C = CrystalOfLetters(['A', 5])
sage: C.latex_file('/tmp/test.tex') #optional requires dot2tex
Use C.metapost(“filename.mp”,[options]), where options can be:
thicklines = True (for thicker edges) labels = False (to suppress labeling of the vertices) scaling_factor=value, where value is a floating point number, 1.0 by default. Increasing or decreasing the scaling factor changes the size of the image. tallness=1.0. Increasing makes the image taller without increasing the width.
Root operators e(1) or f(1) move along red lines, e(2) or f(2) along green. The highest weight is in the lower left. Vertices with the same weight are kept close together. The concise labels on the nodes are strings introduced by Berenstein and Zelevinsky and Littelmann; see Littelmann’s paper Cones, Crystals, Patterns, sections 5 and 6.
For Cartan types B2 or C2, the pattern has the form
a2 a3 a4 a1
where c*a2 = a3 = 2*a4 =0 and a1=0, with c=2 for B2, c=1 for C2. Applying e(2) a1 times, e(1) a2 times, e(2) a3 times, e(1) a4 times returns to the highest weight. (Observe that Littelmann writes the roots in opposite of the usual order, so our e(1) is his e(2) for these Cartan types.) For type A2, the pattern has the form
a3 a2 a1
where applying e(1) a1 times, e(2) a2 times then e(3) a1 times returns to the highest weight. These data determine the vertex and may be translated into a Gelfand-Tsetlin pattern or tableau.
EXAMPLES:
sage: C = CrystalOfLetters(['A', 2])
sage: C.metapost('/tmp/test.mp') #optional
sage: C = CrystalOfLetters(['A', 5])
sage: C.metapost('/tmp/test.mp')
...
NotImplementedError
Returns the plot of self as a directed graph.
EXAMPLES:
sage: C = CrystalOfLetters(['A', 5])
sage: show_default(False) #do not show the plot by default
sage: C.plot()
Graphics object consisting of 17 graphics primitives
Returns the weight lattice realization for the root system associated to self. This default implementation uses the ambient space of the root system.
EXAMPLES:
sage: C = CrystalOfLetters(['A', 5])
sage: C.weight_lattice_realization()
Ambient space of the Root system of type ['A', 5]
sage: K = KirillovReshetikhinCrystal(['A',2,1], 1, 1)
sage: K.weight_lattice_realization()
Weight lattice of the Root system of type ['A', 2, 1]
EXAMPLES:
sage: Crystals().super_categories()
[Category of enumerated sets]