Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Category Theory »

Bases: sage.categories.category.Category
The category of Coxeter groups.
A Coxeter group is a group 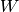 with a distinguished (finite)
family of involutions
with a distinguished (finite)
family of involutions 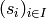 , called the simple
reflections, subject to relations of the form
, called the simple
reflections, subject to relations of the form 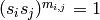 .
.
 is the index set of
is the index set of 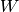 and
and 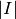 is the rank of
is the rank of 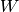 .
.
See http://en.wikipedia.org/wiki/Coxeter_group for details.
EXAMPLES:
sage: C = CoxeterGroups()
sage: C # todo: uppercase for Coxeter
Category of coxeter groups
sage: C.super_categories()
[Category of groups]
sage: W = C.example(); W
The symmetric group on {0, ..., 3}
sage: W.simple_reflections()
Finite family {0: (1, 0, 2, 3), 1: (0, 2, 1, 3), 2: (0, 1, 3, 2)}
Here are some further examples:
sage: FiniteCoxeterGroups().example()
The 5-th dihedral group of order 10
sage: FiniteWeylGroups().example()
The symmetric group on {0, ..., 3}
sage: WeylGroup(["B", 3])
Weyl Group of type ['B', 3] (as a matrix group acting on the ambient space)
Those will eventually be also in this category:
sage: SymmetricGroup(4)
Symmetric group of order 4! as a permutation group
sage: DihedralGroup(5)
Dihedral group of order 10 as a permutation group
TODO: add a demo of usual computations on Coxeter groups.
SEE ALSO: WeylGroups, sage.combinat.root_system
TESTS:
sage: W = CoxeterGroups().example(); TestSuite(W).run(verbose = "True")
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
Running the test suite of self.an_element()
running ._test_category() . . . pass
running ._test_eq() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
pass
running ._test_elements_eq() . . . pass
running ._test_enumerated_set_contains() . . . pass
running ._test_enumerated_set_iter_cardinality() . . . pass
running ._test_enumerated_set_iter_list() . . . pass
running ._test_eq() . . . pass
running ._test_has_descent() . . . pass
running ._test_inverse() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_one() . . . pass
running ._test_pickling() . . . pass
running ._test_prod() . . . pass
running ._test_reduced_word() . . . pass
running ._test_simple_projections() . . . pass
running ._test_some_elements() . . . pass
Returns the result of the application of the simple
projection 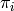 (resp.
(resp. 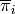 ) on self.
) on self.
See CoxeterGroups.ParentMethods.simple_projections() for the definition of the simple projections.
EXAMPLE:
sage: W=CoxeterGroups().example()
sage: w=W.an_element()
sage: w
(1, 2, 3, 0)
sage: w.apply_simple_projection(2)
(1, 2, 3, 0)
sage: w.apply_simple_projection(2, toward_max=False)
(1, 2, 0, 3)
Returns the result of the (left/right) multiplication of word to self. self is not changed.
EXAMPLE:
sage: W=CoxeterGroups().example()
sage: w=W.an_element()
sage: w
(1, 2, 3, 0)
sage: w.apply_simple_reflections([0,1])
(2, 3, 1, 0)
sage: w
(1, 2, 3, 0)
sage: w.apply_simple_reflections([0,1],side='left')
(0, 1, 3, 2)
Returns the set of all the factorizations 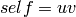 such
that
such
that 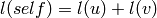 .
.
Iterating through this set is Constant Amortized Time
(counting arithmetic operations in the coxeter group as
constant time) complexity, and memory linear in the length
of 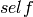 .
.
One can pass as optional argument a predicate p such that
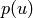 implies
implies 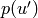 for any
for any  left factor of
left factor of 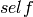 and
and 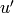 left factor of
left factor of  . Then this returns only the
factorizations
. Then this returns only the
factorizations 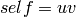 such
such 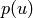 holds.
holds.
Bruhat comparison
INPUT:
- other - an element of the same Coxeter group
OUTPUT: a boolean
Returns whether self <= other in the Bruhat order.
EXAMPLES:
sage: W = WeylGroup(["A",3])
sage: u = W.from_reduced_word([1,2,1])
sage: v = W.from_reduced_word([1,2,3,2,1])
sage: u.bruhat_le(u)
True
sage: u.bruhat_le(v)
True
sage: v.bruhat_le(u)
False
sage: v.bruhat_le(v)
True
sage: s = W.simple_reflections()
sage: s[1].bruhat_le(W.one())
False
The implementation uses the equivalent condition that any reduced word for other contains a reduced word for self as subword. See Stembridge, A short derivation of the Mobius function for the Bruhat order. J. Algebraic Combin. 25 (2007), no. 2, 141–148, Proposition 1.1.
Complexity: 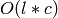 , where
, where 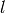 is the minimum of the
lengths of
is the minimum of the
lengths of  and of
and of  , and
, and  is the cost of the low
level methods first_descent(), has_descent(),
apply_simple_reflection(), etc. Those are typically
is the cost of the low
level methods first_descent(), has_descent(),
apply_simple_reflection(), etc. Those are typically
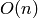 , where
, where  is the rank of the Coxeter group.
is the rank of the Coxeter group.
TESTS:
We now run consistency tests with permutations and bruhat_lower_covers():
sage: W = WeylGroup(["A",3])
sage: P4 = Permutations(4)
sage: def P4toW(w): return W.from_reduced_word(w.reduced_word())
sage: for u in P4:
... for v in P4:
... assert u.bruhat_lequal(v) == P4toW(u).bruhat_le(P4toW(v))
sage: W = WeylGroup(["B",3])
sage: P = W.bruhat_poset() # This is built from bruhat_lower_covers
sage: Q = Poset((W, attrcall("bruhat_le"))) # long time (10s)
sage: all( u.bruhat_le(v) == (P(u) <= P(v)) for u in W for v in W ) # long time (7s)
True
sage: all((P(u) <= P(v)) == (Q(u) <= Q(v)) for u in W for v in W) # long time (9s)
True
Returns all elements that self covers in (strong) Bruhat order.
If w = self has a descent at  , then the elements that
, then the elements that
 covers are exactly
covers are exactly 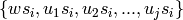 ,
where the
,
where the 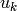 are elements that
are elements that 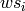 covers that also
do not have a descent at
covers that also
do not have a descent at  .
.
EXAMPLES:
sage: W = WeylGroup(["A",3])
sage: w = W.from_reduced_word([3,2,3])
sage: print([v.reduced_word() for v in w.bruhat_lower_covers()])
[[3, 2], [2, 3]]
sage: W = WeylGroup(["A",3])
sage: print([v.reduced_word() for v in W.simple_reflection(1).bruhat_lower_covers()])
[[]]
sage: print([v.reduced_word() for v in W.one().bruhat_lower_covers()])
[]
sage: W = WeylGroup(["B",4,1])
sage: w = W.from_reduced_word([0,2])
sage: print([v.reduced_word() for v in w.bruhat_lower_covers()])
[[2], [0]]
We now show how to construct the Bruhat poset:
sage: W = WeylGroup(["A",3])
sage: covers = tuple([u, v] for v in W for u in v.bruhat_lower_covers() )
sage: P = Poset((W, covers), cover_relations = True)
sage: P.show()
Alternatively, one can just use:
sage: P = W.bruhat_poset()
The algorithm is taken from Stembridge’s coxeter/weyl package for Maple.
Returns the unique shortest element of the coxeter group
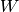 which is in the same left (resp. right) coset as
self, with respect to the parabolic subgroup
which is in the same left (resp. right) coset as
self, with respect to the parabolic subgroup 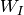 .
.
Returns the descents of self, as a list of elements of the index_set.
The index_set option can be used to restrict to the parabolic subgroup indexed by index_set.
If positive is True, then returns the non-descents instead
TODO: find a better name for positive: complement? non_descent?
Caveat: the return type may change to some other iterable (tuple, ...) in the future. Please use keyword arguments also, as the order of the arguments may change as well.
EXAMPLES:
sage: W=CoxeterGroups().example()
sage: s=W.simple_reflections()
sage: w=s[0]*s[1]
sage: w.descents()
[1]
sage: w=s[0]*s[2]
sage: w.descents()
[0, 2]
TODO: side, index_set, positive
Returns the first left (resp. right) descent of self, as ane element of index_set, or None if there is none.
See descents() for a description of the options.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: s = W.simple_reflections()
sage: w = s[2]*s[0]
sage: w.first_descent()
0
sage: w = s[0]*s[2]
sage: w.first_descent()
0
sage: w = s[0]*s[1]
sage: w.first_descent()
1
Returns whether i is a (left/right) descent of self.
See descents() for a description of the options.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: s = W.simple_reflections()
sage: w = s[0] * s[1] * s[2]
sage: w.has_descent(2)
True
sage: [ w.has_descent(i) for i in [0,1,2] ]
[False, False, True]
sage: [ w.has_descent(i, side = 'left') for i in [0,1,2] ]
[True, False, False]
sage: [ w.has_descent(i, positive = True) for i in [0,1,2] ]
[True, True, False]
This default implementation delegates the work to has_left_descent() and has_right_descent().
Returns whether  is a left descent of self.
is a left descent of self.
This default implementation uses that a left descent of
 is a right descent of
is a right descent of 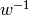 .
.
Returns whether i is a right descent of self.
# EXAMPLES:: # # sage:
Returns the inverse of self
EXAMPLES:
sage: W=WeylGroup(['B',7])
sage: w=W.an_element()
sage: u=w.inverse()
sage: u==~w
True
sage: u*w==w*u
True
sage: u*w
[1 0 0 0 0 0 0]
[0 1 0 0 0 0 0]
[0 0 1 0 0 0 0]
[0 0 0 1 0 0 0]
[0 0 0 0 1 0 0]
[0 0 0 0 0 1 0]
[0 0 0 0 0 0 1]
Returns the length of self, that is the minimal length of a product of simple reflections giving self.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: s1 = W.simple_reflection(1)
sage: s2 = W.simple_reflection(2)
sage: s1.length()
1
sage: (s1*s2).length()
2
sage: W = CoxeterGroups().example()
sage: s = W.simple_reflections()
sage: w = s[0]*s[1]*s[0]
sage: w.length()
3
sage: W = CoxeterGroups().example()
sage: sum((x^w.length()) for w in W) - expand(prod(sum(x^i for i in range(j+1)) for j in range(4))) # This is scandalously slow!!!
0
SEE ALSO: reduced_word()
TODO: Should use reduced_word_iterator (or reverse_iterator)
Returns all elements that self covers in weak order.
INPUT:
- side - ‘left’ or ‘right’ (default: ‘right’)
- index_set - a list of indices or None
OUTPUT: a list
EXAMPLES:
sage: W = WeylGroup(['A',3])
sage: w = W.from_reduced_word([3,2,1])
sage: [x.reduced_word() for x in w.lower_covers()]
[[3, 2]]
To obtain covers for left weak order, set the option side to ‘left’:
sage: [x.reduced_word() for x in w.lower_covers(side='left')]
[[2, 1]]
sage: w = W.from_reduced_word([3,2,3,1])
sage: [x.reduced_word() for x in w.lower_covers()]
[[2, 3, 2], [3, 2, 1]]
Covers w.r.t. a parabolic subgroup are obtained with the option index_set:
sage: [x.reduced_word() for x in w.lower_covers(index_set = [1,2])]
[[2, 3, 2]]
sage: [x.reduced_word() for x in w.lower_covers(side='left')]
[[3, 2, 1], [2, 3, 1]]
Returns a reduced word for self.
This is a word ![[i_1,i_2,\ldots,i_k]](../../_images/math/1d1c8f2389e8da5198a7ee60e4955f97dd3d663e.png) of minimal length
such that
of minimal length
such that 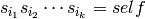 , where
, where  are the simple reflections.
are the simple reflections.
EXAMPLES:
sage: W=CoxeterGroups().example()
sage: s=W.simple_reflections()
sage: w=s[0]*s[1]*s[2]
sage: w.reduced_word()
[0, 1, 2]
sage: w=s[0]*s[2]
sage: w.reduced_word()
[2, 0]
SEE ALSO: reduced_words(), reduced_word_reverse_iterator(), length()
Returns a reverse iterator on a reduced word for self.
EXAMPLES:
sage: W=CoxeterGroups().example()
sage: s = W.simple_reflections()
sage: sigma = s[0]*s[1]*s[2]
sage: rI=sigma.reduced_word_reverse_iterator()
sage: [i for i in rI]
[2, 1, 0]
sage: s[0]*s[1]*s[2]==sigma
True
sage: sigma.length()
3
SEE ALSO reduced_word()
Default implementation: recursively remove the first right descent until the identity is reached (see first_descent() and apply_simple_reflection()).
Returns all reduced words for self.
EXAMPLES:
sage: W=CoxeterGroups().example()
sage: s=W.simple_reflections()
sage: w=s[0]*s[2]
sage: w.reduced_words()
[[2, 0], [0, 2]]
sage: W=WeylGroup(['E',6])
sage: w=W.from_reduced_word([2,3,4,2])
sage: w.reduced_words()
[[3, 2, 4, 2], [2, 3, 4, 2], [3, 4, 2, 4]]
TODO: the result should be full featured finite enumerated set (e.g. counting can be done much faster than iterating).
Returns all elements that cover self in weak order.
INPUT:
- side - ‘left’ or ‘right’ (default: ‘right’)
- index_set - a list of indices or None
OUTPUT: a list
EXAMPLES:
sage: W = WeylGroup(['A',3])
sage: w = W.from_reduced_word([2,3])
sage: [x.reduced_word() for x in w.upper_covers()]
[[2, 3, 1], [2, 3, 2]]
To obtain covers for left weak order, set the option side to ‘left’:
sage: [x.reduced_word() for x in w.upper_covers(side = 'left')]
[[1, 2, 3], [2, 3, 2]]
Covers w.r.t. a parabolic subgroup are obtained with the option index_set:
sage: [x.reduced_word() for x in w.upper_covers(index_set = [1])]
[[2, 3, 1]]
sage: [x.reduced_word() for x in w.upper_covers(side = 'left', index_set = [1])]
[[1, 2, 3]]
Returns all elements that self covers in weak order.
INPUT:
- side - ‘left’ or ‘right’ (default: ‘right’)
- positive - a boolean (default: False)
- index_set - a list of indices or None
OUTPUT: a list
EXAMPLES:
sage: W = WeylGroup(['A',3])
sage: w = W.from_reduced_word([3,2,1])
sage: [x.reduced_word() for x in w.weak_covers()]
[[3, 2]]
To obtain instead elements that cover self, set positive = True:
sage: [x.reduced_word() for x in w.weak_covers(positive = True)]
[[3, 1, 2, 1], [2, 3, 2, 1]]
To obtain covers for left weak order, set the option side to ‘left’:
sage: [x.reduced_word() for x in w.weak_covers(side='left')]
[[2, 1]]
sage: w = W.from_reduced_word([3,2,3,1])
sage: [x.reduced_word() for x in w.weak_covers()]
[[2, 3, 2], [3, 2, 1]]
sage: [x.reduced_word() for x in w.weak_covers(side='left')]
[[3, 2, 1], [2, 3, 1]]
Covers w.r.t. a parabolic subgroup are obtained with the option index_set:
sage: [x.reduced_word() for x in w.weak_covers(index_set = [1,2])]
[[2, 3, 2]]
comparison in weak order
INPUT:
- other - an element of the same Coxeter group
- side - ‘left’ or ‘right’ (default: ‘right’)
OUTPUT: a boolean
Returns whether self <= other in left (resp. right) weak order, that is if ‘v’ can be obtained from ‘v’ by length increasing multiplication by simple reflections on the left (resp. right).
EXAMPLES:
sage: W = WeylGroup(["A",3])
sage: u = W.from_reduced_word([1,2])
sage: v = W.from_reduced_word([1,2,3,2])
sage: u.weak_le(u)
True
sage: u.weak_le(v)
True
sage: v.weak_le(u)
False
sage: v.weak_le(v)
True
Comparison for left weak order is achieved with the option side:
sage: u.weak_le(v, side = 'left')
False
The implementation uses the equivalent condition that any
reduced word for  is a right (resp. left) prefix of
some reduced word for
is a right (resp. left) prefix of
some reduced word for  .
.
Complexity: 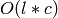 , where
, where 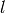 is the minimum of the
lengths of
is the minimum of the
lengths of  and of
and of  , and
, and  is the cost of the low
level methods first_descent(), has_descent(),
apply_simple_reflection(). Those are typically
is the cost of the low
level methods first_descent(), has_descent(),
apply_simple_reflection(). Those are typically
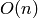 , where
, where  is the rank of the Coxeter group.
is the rank of the Coxeter group.
We now run consistency tests with permutations:
sage: W = WeylGroup(["A",3])
sage: P4 = Permutations(4)
sage: def P4toW(w): return W.from_reduced_word(w.reduced_word())
sage: for u in P4:
... for v in P4:
... assert u.permutohedron_lequal(v) == P4toW(u).weak_le(P4toW(v))
... assert u.permutohedron_lequal(v, side='left') == P4toW(u).weak_le(P4toW(v), side='left')
Implements: Sets.ParentMethods.an_element() by returning the product of the simple reflections (a Coxeter element).
EXAMPLES:
sage: W=CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: W.an_element()
(1, 2, 3, 0)
Implements: Sets.ParentMethods.an_element() by returning the product of the simple reflections (a Coxeter element).
EXAMPLES:
sage: W=CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: W.an_element()
(1, 2, 3, 0)
Returns the list of t such that x <= t <= y.
EXAMPLES:
sage: W = WeylGroup("A3", prefix="s")
sage: [s1,s2,s3]=W.simple_reflections()
sage: W.bruhat_interval(s2,s1*s3*s2*s1*s3)
[s1*s2*s3*s2*s1, s2*s3*s2*s1, s3*s1*s2*s1, s1*s2*s3*s1, s1*s2*s3*s2, s3*s2*s1, s2*s3*s1, s2*s3*s2, s1*s2*s1, s3*s1*s2, s1*s2*s3, s2*s1, s3*s2, s2*s3, s1*s2, s2]
sage: W = WeylGroup(['A',2,1], prefix="s")
sage: [s0,s1,s2]=W.simple_reflections()
sage: W.bruhat_interval(1,s0*s1*s2)
[s0*s1*s2, s1*s2, s0*s2, s0*s1, s2, s1, s0, 1]
INPUT:
- word - a list (or iterable) of elements of self.index_set()
Returns the group element corresponding to the given
word. Namely, if word is ![[i_1,i_2,\ldots,i_k]](../../_images/math/1d1c8f2389e8da5198a7ee60e4955f97dd3d663e.png) , then
this returns the corresponding product of simple
reflections
, then
this returns the corresponding product of simple
reflections 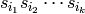 .
.
Note: the main use case is for constructing elements from reduced words, hence the name of this method. But actually the input word need not be reduced.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: s = W.simple_reflections()
sage: W.from_reduced_word([0,2,0,1])
(0, 3, 1, 2)
sage: W.from_reduced_word((0,2,0,1))
(0, 3, 1, 2)
sage: s[0]*s[2]*s[0]*s[1]
(0, 3, 1, 2)
See also :meth:’._test_reduced_word’:
sage: W._test_reduced_word()
TESTS:
sage: W=WeylGroup(['E',6])
sage: W.from_reduced_word([2,3,4,2])
[ 0 1 0 0 0 0 0 0]
[ 0 0 -1 0 0 0 0 0]
[-1 0 0 0 0 0 0 0]
[ 0 0 0 1 0 0 0 0]
[ 0 0 0 0 1 0 0 0]
[ 0 0 0 0 0 1 0 0]
[ 0 0 0 0 0 0 1 0]
[ 0 0 0 0 0 0 0 1]
Implements Groups.ParentMethods.group_generators() by returning the simple reflections of self.
EXAMPLES:
sage: D10 = FiniteCoxeterGroups().example(10)
sage: D10.group_generators()
Finite family {1: (1,), 2: (2,)}
sage: SymmetricGroup(5).group_generators()
Finite family {1: (1,2), 2: (2,3), 3: (3,4), 4: (4,5)}
Those give semigroup generators, even for an infinite group:
sage: W = WeylGroup(["A",2,1])
sage: W.semigroup_generators()
Finite family {0: [-1 1 1]
[ 0 1 0]
[ 0 0 1],
1: [ 1 0 0]
[ 1 -1 1]
[ 0 0 1],
2: [ 1 0 0]
[ 0 1 0]
[ 1 1 -1]}
Implements Groups.ParentMethods.group_generators() by returning the simple reflections of self.
EXAMPLES:
sage: D10 = FiniteCoxeterGroups().example(10)
sage: D10.group_generators()
Finite family {1: (1,), 2: (2,)}
sage: SymmetricGroup(5).group_generators()
Finite family {1: (1,2), 2: (2,3), 3: (3,4), 4: (4,5)}
Those give semigroup generators, even for an infinite group:
sage: W = WeylGroup(["A",2,1])
sage: W.semigroup_generators()
Finite family {0: [-1 1 1]
[ 0 1 0]
[ 0 0 1],
1: [ 1 0 0]
[ 1 -1 1]
[ 0 0 1],
2: [ 1 0 0]
[ 0 1 0]
[ 1 1 -1]}
Returns the simple projection 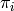 (or
(or 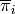 if toward_max is False).
if toward_max is False).
See simple_projections() for the options. and for the definition of the simple projections.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: s = W.simple_reflections()
sage: sigma=W.an_element()
sage: sigma
(1, 2, 3, 0)
sage: u0=W.simple_projection(0)
sage: d0=W.simple_projection(0,toward_max=False)
sage: sigma.length()
3
sage: pi=sigma*s[0]
sage: pi.length()
4
sage: u0(sigma)
(2, 1, 3, 0)
sage: pi
(2, 1, 3, 0)
sage: u0(pi)
(2, 1, 3, 0)
sage: d0(sigma)
(1, 2, 3, 0)
sage: d0(pi)
(1, 2, 3, 0)
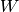
Returns the simple projections of 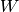 , as a family.
, as a family.
To each simple reflection 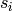 of
of 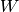 , corresponds a
simple projection
, corresponds a
simple projection 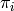 from
from 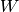 to
to 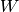 defined by:
defined by:
if
is not a descent of

otherwise.
The simple projections 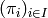 move elements
down the right permutohedron, toward the maximal element.
They satisfy the same relations as the simple reflections,
except that
move elements
down the right permutohedron, toward the maximal element.
They satisfy the same relations as the simple reflections,
except that 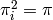 , whereas
, whereas 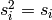 . As such,
the simple projections generate the
. As such,
the simple projections generate the  -Hecke monoid.
-Hecke monoid.
By symmetry, one can also define the projections
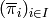 (option toward_max):
(option toward_max):
if
is a descent of

otherwise.
as well as the analogues acting on the left (option side).
TODO: the name 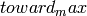 is not explicit and
should/will be replaced; suggestions welcome.
is not explicit and
should/will be replaced; suggestions welcome.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: s = W.simple_reflections()
sage: sigma=W.an_element()
sage: sigma
(1, 2, 3, 0)
sage: pi=W.simple_projections()
sage: pi
Finite family {0: <function <lambda> at ...>, 1: <function <lambda> at ...>, 2: <function <lambda> ...>}
sage: pi[1](sigma)
(1, 3, 2, 0)
sage: W.simple_projection(1)(sigma)
(1, 3, 2, 0)
INPUT: - i - an element from the index set.
Returns the simple reflection 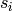
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: W.simple_reflection(1)
(0, 2, 1, 3)
sage: s = W.simple_reflections()
sage: s[1]
(0, 2, 1, 3)
Returns the simple reflections 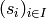 , as a family.
, as a family.
EXAMPLES:
sage: W = CoxeterGroups().example()
sage: W
The symmetric group on {0, ..., 3}
sage: s = W.simple_reflections()
sage: s
Finite family {0: (1, 0, 2, 3), 1: (0, 2, 1, 3), 2: (0, 1, 3, 2)}
sage: s[0]
(1, 0, 2, 3)
sage: s[1]
(0, 2, 1, 3)
sage: s[2]
(0, 1, 3, 2)
This default implementation uses index_set() and simple_reflection().
Implements Sets.ParentMethods.some_elements() by
returning some typical element of 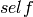 .
.
EXAMPLES:
sage: W=WeylGroup(['A',3])
sage: W.some_elements()
[[0 1 0 0]
[1 0 0 0]
[0 0 1 0]
[0 0 0 1],
[1 0 0 0]
[0 0 1 0]
[0 1 0 0]
[0 0 0 1],
[1 0 0 0]
[0 1 0 0]
[0 0 0 1]
[0 0 1 0],
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1],
[0 1 0 0]
[1 0 0 0]
[0 0 1 0]
[0 0 0 1]]
sage: W.order()
24
EXAMPLES:
sage: CoxeterGroups().super_categories()
[Category of groups]