Bases: sage.combinat.free_module.CombinatorialFreeModule
INPUT:
- W – A CoxeterGroup or CartanType
- q1 – a parameter.
OPTIONAL ARGUMENTS:
- q2 – another parameter (default -1)
- base_ring – A ring containing q1 and q2 (default q1.parent())
- prefix – a label for the generators (default “T”)
The Iwahori Hecke algebra is defined in:
Nagayoshi Iwahori, On the structure of a Hecke ring of a Chevalley group over a finite field. J. Fac. Sci. Univ. Tokyo Sect. I 10 1964 215–236 (1964).
The Iwahori Hecke algebra is a deformation of the group algebra of
the Weyl/Coxeter group. Taking the deformation parameter 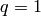 as in the
following example gives a ring isomorphic to that group
algebra. The parameter
as in the
following example gives a ring isomorphic to that group
algebra. The parameter  is a deformation parameter.
is a deformation parameter.
EXAMPLES:
sage: H = IwahoriHeckeAlgebraT("A3",1,prefix = "s")
sage: [s1,s2,s3] = H.algebra_generators()
sage: s1*s2*s3*s1*s2*s1 == s3*s2*s1*s3*s2*s3
True
sage: w0 = H(H.coxeter_group().long_element())
sage: w0
s1*s2*s3*s1*s2*s1
sage: H.an_element()
3*s1*s2 + 3*s1 + 1
Iwahori Hecke algebras have proved to be fundamental. See for example:
Kazhdan and Lusztig, Representations of Coxeter groups and Hecke algebras. Invent. Math. 53 (1979), no. 2, 165–184.
Iwahori-Hecke Algebras: Thomas J. Haines, Robert E. Kottwitz, Amritanshu Prasad, http://front.math.ucdavis.edu/0309.5168
V. Jones, Hecke algebra representations of braid groups and link polynomials. Ann. of Math. (2) 126 (1987), no. 2, 335–388.
For every simple reflection 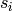 of the Coxeter group, there is a
corresponding generator
of the Coxeter group, there is a
corresponding generator 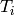 of the Iwahori Hecke algebra. These
are subject to the relations
of the Iwahori Hecke algebra. These
are subject to the relations
together with the braid relations 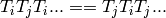 ,
where the number of terms on both sides is
,
where the number of terms on both sides is 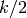 with
with  the order of
the order of
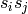 in the Coxeter group.
in the Coxeter group.
Weyl group elements form a basis of the Iwahori Hecke algebra 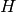 with the property that if
with the property that if 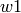 and
and 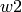 are Coxeter group elements
such that (w1*w2).length() == w1.length() + w2.length() then
H(w1*w2) == H(w1)*H(w2).
are Coxeter group elements
such that (w1*w2).length() == w1.length() + w2.length() then
H(w1*w2) == H(w1)*H(w2).
With the default value 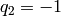 and with
and with 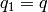 the
generating relation may be written
the
generating relation may be written 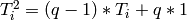 as in
Iwahori’s paper.
as in
Iwahori’s paper.
EXAMPLES:
sage: R.<q>=PolynomialRing(ZZ)
sage: H=IwahoriHeckeAlgebraT("B3",q); H
The Iwahori Hecke Algebra of Type B3 in q,-1 over Univariate Polynomial Ring in q over Integer Ring and prefix T
sage: T1,T2,T3 = H.algebra_generators()
sage: T1*T1
(q-1)*T1 + q
It is useful to define T1,T2,T3 = H.algebra_generators() as above so that H can parse its own output:
sage: H(T1)
T1
The Iwahori Hecke algebra associated with an affine Weyl group is called an affine Hecke algebra. These may be implemented as follows:
sage: R.<q>=QQ[]
sage: H=IwahoriHeckeAlgebraT(['A',2,1],q)
sage: [T0,T1,T2]=H.algebra_generators()
sage: T1*T2*T1*T0*T1*T0
(q-1)*T1*T2*T0*T1*T0 + q*T1*T2*T0*T1
sage: T1*T2*T1*T0*T1*T1
q*T1*T2*T1*T0 + (q-1)*T1*T2*T0*T1*T0
sage: T1*T2*T1*T0*T1*T2
T1*T2*T0*T1*T0*T2
sage: (T1*T2*T0*T1*T0*T2).support_of_term() # get the underlying Weyl group element
[ 2 1 -2]
[ 3 1 -3]
[ 2 2 -3]
sage: R = IwahoriHeckeAlgebraT("A3",0,0,prefix = "s")
sage: [s1,s2,s3] = R.algebra_generators()
sage: s1*s1
0
TESTS:
sage: H1 = IwahoriHeckeAlgebraT("A2",1)
sage: H2 = IwahoriHeckeAlgebraT("A2",1)
sage: H3 = IwahoriHeckeAlgebraT("A2",-1)
sage: H1 == H1, H1 == H2, H1 is H2
(True, True, True)
sage: H1 == H3
False
sage: R.<q>=PolynomialRing(QQ)
sage: IwahoriHeckeAlgebraT("A3",q).base_ring() == R
True
sage: R.<q>=QQ[]; H=IwahoriHeckeAlgebraT("A2",q)
sage: 1+H(q)
(q+1)
sage: R.<q>=QQ[]
sage: H = IwahoriHeckeAlgebraT("A2",q)
sage: T1,T2 = H.algebra_generators()
sage: H(T1+2*T2)
T1 + 2*T2
Design discussion
This is a preliminary implementation. For work in progress, see: http://wiki.sagemath.org/HeckeAlgebras.
- Should we use q in QQ[‘q’] as default parameter for q_1?
Bases: sage.combinat.free_module.CombinatorialFreeModuleElement
A class for elements of an IwahoriHeckeAlgebra
TESTS:
sage: R.<q>=QQ[]
sage: H=IwahoriHeckeAlgebraT("B3",q)
sage: [T1, T2, T3] = H.algebra_generators()
sage: T1+2*T2*T3
T1 + 2*T2*T3
sage: R.<q1,q2>=QQ[]
sage: H=IwahoriHeckeAlgebraT("A2",q1,q2,prefix="x")
sage: sum(H.algebra_generators())^2
x1*x2 + x2*x1 + (q1+q2)*x1 + (q1+q2)*x2 + (-2*q1*q2)
sage: H=IwahoriHeckeAlgebraT("A2",q1,q2,prefix="t")
sage: [t1,t2] = H.algebra_generators()
sage: (t1-t2)^3
(q1^2-q1*q2+q2^2)*t1 + (-q1^2+q1*q2-q2^2)*t2
sage: R.<q>=QQ[]
sage: H=IwahoriHeckeAlgebraT("G2",q)
sage: [T1, T2] = H.algebra_generators()
sage: T1*T2*T1*T2*T1*T2 == T2*T1*T2*T1*T2*T1
True
sage: T1*T2*T1 == T2*T1*T2
False
sage: H = IwahoriHeckeAlgebraT("A2",1)
sage: [T1,T2]=H.algebra_generators()
sage: T1+T2
T1 + T2
sage: -(T1+T2)
-T1 - T2
sage: 1-T1
-T1 + 1
sage: T1.parent()
The Iwahori Hecke Algebra of Type A2 in 1,-1 over Integer Ring and prefix T
If the element is a basis element, that is, an element of the form self(w) with w in the Weyl group, this method computes its inverse. The base ring must be a field or Laurent polynomial ring. Other elements of the ring have inverses but the inverse method is only implemented for the basis elements.
EXAMPLES:
sage: R.<q>=LaurentPolynomialRing(QQ)
sage: H = IwahoriHeckeAlgebraT("A2",q)
sage: [T1,T2]=H.algebra_generators()
sage: x = (T1*T2).inverse(); x
(q^-2)*T2*T1 + (-q^-1+q^-2)*T1 + (-q^-1+q^-2)*T2 + (1-2*q^-1+q^-2)
sage: x*T1*T2
1
EXAMPLES
sage: R.<q>=QQ[]
sage: H = IwahoriHeckeAlgebraT("A3",q)
sage: [H.algebra_generator(i) for i in H.index_set()]
[T1, T2, T3]
Returns the generators. They do not have order two but satisfy
a quadratic relation. They coincide with the simple
reflections in the Coxeter group when 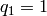 and
and 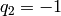 . In
this special case, the Iwahori Hecke algebra is identified
with the group algebra of the Coxeter group.
. In
this special case, the Iwahori Hecke algebra is identified
with the group algebra of the Coxeter group.
EXAMPLES
sage: R.<q>=QQ[]
sage: H = IwahoriHeckeAlgebraT("A3",q)
sage: T=H.algebra_generators(); T
Finite family {1: T1, 2: T2, 3: T3}
sage: T.list()
[T1, T2, T3]
sage: [T[i] for i in [1,2,3]]
[T1, T2, T3]
sage: [T1, T2, T3] = H.algebra_generators()
sage: T1
T1
sage: H = IwahoriHeckeAlgebraT(['A',2,1],q)
sage: T=H.algebra_generators(); T
Finite family {0: T0, 1: T1, 2: T2}
sage: T.list()
[T0, T1, T2]
sage: [T[i] for i in [0,1,2]]
[T0, T1, T2]
sage: [T0, T1, T2] = H.algebra_generators()
sage: T0
T0
EXAMPLES
sage: IwahoriHeckeAlgebraT("D4",0).cartan_type()
['D', 4]
EXAMPLES:
sage: IwahoriHeckeAlgebraT("B2",1).coxeter_group()
Weyl Group of type ['B', 2] (as a matrix group acting on the ambient space)
EXAMPLES:
sage: IwahoriHeckeAlgebraT("B2",1).index_set()
[1, 2]
This method is only available if q1 and q2 are invertible. In that case, the algebra generators are also invertible and this method returns the inverse of self.algebra_generator(i). The base ring should be either a field or a Laurent polynomial ring.
EXAMPLES:
sage: P.<q1,q2>=QQ[]
sage: F=Frac(P)
sage: H = IwahoriHeckeAlgebraT("A2",q1,q2,base_ring=F)
sage: H.base_ring()
Fraction Field of Multivariate Polynomial Ring in q1, q2 over Rational Field
sage: H.inverse_generator(1)
((-1)/(q1*q2))*T1 + ((q1+q2)/(q1*q2))
sage: H = IwahoriHeckeAlgebraT("A2",q1,-1,base_ring=F)
sage: H.inverse_generator(2)
((-1)/(-q1))*T2 + ((q1-1)/(-q1))
sage: P1.<r1,r2>=LaurentPolynomialRing(QQ)
sage: H1 = IwahoriHeckeAlgebraT("B2",r1,r2,base_ring=P1)
sage: H1.base_ring()
Multivariate Laurent Polynomial Ring in r1, r2 over Rational Field
sage: H1.inverse_generator(2)
(-r1^-1*r2^-1)*T2 + (r2^-1+r1^-1)
sage: H2 = IwahoriHeckeAlgebraT("C2",r1,-1,base_ring=P1)
sage: H2.inverse_generator(2)
(r1^-1)*T2 + (-1+r1^-1)
This method is only available if q1 and q2 are invertible. In that case, the algebra generators are also invertible and this method returns their inverses.
Returns the unit of the underlying Coxeter group, which indexes the one of this algebra, as per AlgebrasWithBasis.ParentMethods.one_basis().
EXAMPLES:
sage: H = IwahoriHeckeAlgebraT("B3", 1)
sage: H.one_basis()
[1 0 0]
[0 1 0]
[0 0 1]
sage: H.one_basis() == H.coxeter_group().one()
True
sage: H.one()
1
Returns T_i*x, where T_i is the i-th generator. This is coded individually for use in x._mul_().
Returns the product 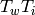 (resp.
(resp. 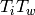 ) if side is “right” (resp. “left”)
) if side is “right” (resp. “left”)
EXAMPLES:
sage: R.<q>=QQ[]; H = IwahoriHeckeAlgebraT("A2",q)
sage: s1,s2 = H.coxeter_group().simple_reflections()
sage: [H.product_by_generator_on_basis(w, 1) for w in [s1,s2,s1*s2]]
[(q-1)*T1 + q, T2*T1, T1*T2*T1]
sage: [H.product_by_generator_on_basis(w, 1, side = "left") for w in [s1,s2,s1*s2]]
[(q-1)*T1 + q, T1*T2, (q-1)*T1*T2 + q*T2]
Returns 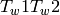 , where
, where 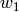 and
and 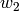 are in the Coxeter group
are in the Coxeter group
EXAMPLES:
sage: R.<q>=QQ[]; H = IwahoriHeckeAlgebraT("A2",q)
sage: s1,s2 = H.coxeter_group().simple_reflections()
sage: [H.product_on_basis(s1,x) for x in [s1,s2]]
[(q-1)*T1 + q, T1*T2]