This chapter discusses some issues with, and advice for, coding in Sage.
If you are planning to develop some new code for Sage, design is important. So think about what your program will do and how that fits into the structure of Sage. In particular, much of Sage is implemented in the object-oriented language Python, and there is a hierarchy of classes that organize code and functionality. For example, if you implement elements of a ring, your class should derive from sage.structure.element.RingElement, rather than starting from scratch. Try to figure out how your code should fit in with other Sage code, and design it accordingly.
Functions with leading and trailing double underscores __XXX__ are all predefined by Python. Functions with leading and trailing single underscores _XXX_ are defined for Sage. Functions with a single leading underscore are meant to be semi-private, and those with a double leading underscore are considered really private. Users can create functions with leading and trailing underscores.
Just as Python has many standard special methods for objects, Sage also has special methods. They are typically of the form _XXX_. (In a few cases, the trailing underscore is not included, but this will be changed so that the trailing underscore is always included.) This section describes these special methods.
All objects in Sage should derive from the Cython extension class SageObject:
from sage.ext.sage_object import SageObject
class MyClass(SageObject,...):
...
or from some other already existing Sage class:
from sage.rings.ring import Algebra
class MyFavoriteAlgebra(Algebra):
...
You should implement the _latex_ and _repr_ method for every object. The other methods depend on the nature of the object.
Every object x in Sage should support the command latex(x), so that any Sage object can be easily and accurately displayed via LaTeX. Here is how to make a class (and therefore its instances) support the command latex.
An example template for a _latex_ method follows:
class X:
...
def _latex_(self):
r"""
Returns the LaTeX representation of X.
EXAMPLES::
sage: a = X(1,2)
sage: latex(a)
'\\frac{1}{2}'
"""
return '\\frac{%s}{%s}'%(latex(self.numer), latex(self.denom))
As shown in the example, latex(a) will produce LaTeX code representing the object a. Calling view(a) will display the typeset version of this.
The standard Python printing method is __repr__(self). In Sage, that is for objects that derive from SageObject (which is everything in Sage), instead define _repr_(self). This is preferable because if you only define _repr_(self) and not __repr__(self), then users can rename your object to print however they like. Also, some objects should print differently depending on the context.
Here is an example of the _latex_ and _repr_ functions for the Pi class. It is from the file SAGE_ROOT/devel/sage/sage/functions/constants.py:
class Pi(Constant):
"""
The ratio of a circle's circumference to its diameter.
EXAMPLES:
sage: pi
pi
sage: float(pi)
3.1415926535897931
"""
...
def _repr_(self):
return "pi"
def _latex_(self):
return "\\pi"
Provide a _matrix_ method for an object that can be coerced to a
matrix over a ring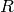 
. Then the Sage function matrix will work
for this object.
The following is from SAGE_ROOT/devel/sage/sage/graphs/graph.py:
class GenericGraph(SageObject):
...
def _matrix_(self, R=None):
if R is None:
return self.am()
else:
return self.am().change_ring(R)
def adjacency_matrix(self, sparse=None, boundary_first=False):
...
Similarly, provide a _vector_ method for an object that can be
coerced to a vector over a ring 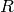. Then the Sage function vector
will work for this object.
The following is from the file SAGE_ROOT/sage/sage/modules/free_module_element.pyx:
cdef class FreeModuleElement(element_Vector): # abstract base class
...
def _vector_(self, R):
return self.change_ring(R)
The following files are relevant to preparsing in Sage:
In particular, the file preparser.py contains the Sage preparser code. The following are some notes from it:
In Sage, methods can be called on integer and real literals. Note that in pure Python this would be a syntax error. For example:
sage: 16.sqrt()
4
sage: 87.factor()
3 * 29
Raw literals are not preparsed, which can be useful from an efficiency point of view. Just like Python ints are denoted by an L, in Sage raw integer and floating literals are followed by an “r” (or “R”) for raw, meaning not preparsed. For example:
sage: a = 393939r
sage: a
393939
sage: type(a)
<type 'int'>
sage: b = 393939
sage: type(b)
<type 'sage.rings.integer.Integer'>
sage: a == b
True
Raw literals can be very useful in certain cases. For instance, Python integers can be more efficient than Sage integers when they are very small. Large Sage integers are much more efficient than Python integers since they are implemented using the GMP C library.
Consult the file preparser.py for more details about Sage preparsing, more examples involving raw literals, etc.
When a file foo.sage is loaded in a Sage session, a preparsed version of foo.sage is created and named foo.py. The beginning of foo.py states:
This file was *autogenerated* from the file foo.sage.
The primary goal of coercion is to be able to transparently do
arithmetic, comparisons, etc. between elements of distinct sets. For
example, when one writes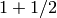 
, one wants to perform arithmetic on
the operands as rational numbers, despite the left term being an
integer. This makes sense given the obvious and natural inclusion of
the integers into the rational numbers. The goal of the coercion
system is to facilitate this (and more complicated arithmetic) without
having to explicitly map everything over into the same domain, and at
the same time being strict enough to not resolve ambiguity or accept
nonsense.
The coercion model for Sage is described in detail, with examples, in the Coercion section of the Sage Reference Manual.
Parent structures (e.g. rings, fields, matrix spaces, etc.) should be immutable and globally unique whenever possible. Immutability means, among other things, that properties like generator labels and default coercion precision cannot be changed.
Global uniqueness while not wasting memory is best implemented using the standard Python weakref module, a factory function, and module scope variable.
Certain objects, e.g. matrices, may start out mutable and become immutable later. See the file SAGE_ROOT/devel/sage/sage/structure/mutability.py.
Here is the definition of __hash__ from the Python reference manual.
Called for the key object for dictionary operations, and by the built-in function hash(). Should return a 32-bit integer usable as a hash value for dictionary operations. The only required property is that objects which compare equal have the same hash value; it is advised to somehow mix together (e.g., using exclusive or) the hash values for the components of the object that also play a part in comparison of objects. If a class does not define a __cmp__() method it should not define a __hash__() operation either; if it defines __cmp__() or __eq__() but not __hash__(), its instances will not be usable as dictionary keys. If a class defines mutable objects and implements a __cmp__() or __eq__() method, it should not implement __hash__(), since the dictionary implementation requires that a key’s hash value is immutable (if the object’s hash value changes, it will be in the wrong hash bucket).
Notice the phrase, “The only required property is that objects which compare equal have the same hash value.” This is an assumption made by the Python language, which in Sage we simply cannot make (!), and violating it has consequences. Fortunately, the consequences are pretty clearly defined and reasonably easy to understand, so if you know about them they do not cause you trouble. The following example illustrates them pretty well:
sage: v = [Mod(2,7)]
sage: 9 in v
True
sage: v = set([Mod(2,7)])
sage: 9 in v
False
sage: 2 in v
True
sage: w = {Mod(2,7):'a'}
sage: w[2]
'a'
sage: w[9]
...
KeyError: 9
Here is another example:
sage: R = RealField(10000)
sage: a = R(1) + R(10)^-100
sage: a == RDF(1) # because the a gets coerced down to RDF
True
but hash(a) should not equal hash(1).
Unfortunately, in Sage we simply cannot require
(#) "a == b ==> hash(a) == hash(b)"
because serious mathematics is simply too complicated for this rule. For example, the equalities z == Mod(z, 2) and z == Mod(z, 3) would force hash() to be constant on the integers.
The only way we could “fix” this problem for good would be to abandon using the == operator for “Sage equality”, and implement Sage equality as a new method attached to each object. Then we could follow Python rules for == and our rules for everything else, and all Sage code would become completely unreadable (and for that matter unwritable). So we just have to live with it.
So what is done in Sage is to attempt to satisfy (#) when it is reasonably easy to do so, but use judgment and not go overboard. For example,
sage: hash(Mod(2,7))
2
The output 2 is better than some random hash that also involves the moduli, but it is of course not right from the Python point of view, since 9 == Mod(2,7).
The goal is to make a hash function that is fast, but within reason respects any obvious natural inclusions and coercions.
Please avoid code like this:
try:
some_code()
except: # bad
more_code()
Instead, catch specific exceptions. For example,
try:
return self.__coordinate_ring
except (AttributeError, OtherExceptions), msg: # Good
more_code_to_compute_something()
Note that the syntax in except is to list all the exceptions that are caught as a tuple, followed by an error message.
If you do not have any exceptions explicitly listed (as a tuple), your code will catch absolutely anything, including ctrl-C, typos in the code, and alarms, and this will lead to confusion. Also, this might catch real errors which should be propagated to the user.
We mention two issues with importing: circular imports and importing large third-party modules.
First, you must avoid circular imports. For example, suppose that the file SAGE_ROOT/devel/sage/sage/algebras/steenrod_algebra.py started with a line
from sage.sage.algebras.steenrod_algebra_bases import *
and that the file SAGE_ROOT/devel/sage/sage/algebras/steenrod_algebra_bases.py started with a line
from sage.sage.algebras.steenrod_algebra import SteenrodAlgebra
This sets up a loop: loading one of these files requires the other, which then requires the first, etc.
With this set-up, running Sage will produce an error:
Exception exceptions.ImportError: 'cannot import name SteenrodAlgebra'
in 'sage.rings.polynomial.polynomial_element.
Polynomial_generic_dense.__normalize' ignored
-------------------------------------------------------------------
ImportError Traceback (most recent call last)
...
ImportError: cannot import name SteenrodAlgebra
Instead, you might replace the import * line at the top of the file by more specific imports where they are needed in the code. For example, the basis method for the class SteenrodAlgebra might look like this (omitting the documentation string):
def basis(self, n):
from steenrod_algebra_bases import steenrod_algebra_basis
return steenrod_algebra_basis(n, basis=self._basis_name, p=self.prime)
Second, do not import at the top level of your module a third-party module that will take a long time to initialize (e.g. matplotlib). As above, you might instead import specific components of the module when they are needed, rather than at the top level of your file.
It is important to try to make from sage.all import * as fast as possible, since this is what dominates the Sage startup time, and controlling the top-level imports helps to do this.
There are several copies of Sage library files, and it can be confusing for beginners to know which one to modify. In the directory SAGE_ROOT/devel/sage, there is a subdirectory build which contains copies of Python files and their byte-compiled versions, along with compiled version of Cython files. These are the files that Sage actually uses, but you never need to touch these. Instead, always work with files in the directory SAGE_ROOT/devel/sage/sage. For example, if you want to add a new method for simplicial complexes, then edit the file SAGE_ROOT/devel/sage/sage/homology/simplicial_complex.py. Save your changes, and then type sage -b to incorporate those changes. This automatically copies the appropriate files into the appropriate places under SAGE_ROOT/devel/sage/build.
You should also read Producing Patches with Mercurial for information about how to create a copy of the Sage library and make your changes there, so that first, it is easy to undo your changes, and second, it is easy to produce a “patch” file so you can share your changes with other people.
If you want to create a new directory in the Sage library SAGE_ROOT/devel/sage/sage (say, measure_theory), that directory should contain an empty file __init__.py in addition to whatever files you want to add (say, borel_measure.py and banach_tarski.py), and also a file all.py listing imports from that directory. The file all.py might look like this:
from borel_measure import BorelMeasure
from banach_tarski import BanachTarskiParadox
Then in the file SAGE_ROOT/devel/sage/sage/all.py, add a line
from sage.measure_theory.all import *
Finally, add the directory name (“measure_theory”) to the packages list in the Distutils section of the file SAGE_ROOT/devel/sage/setup.py: add a line
'sage.measure_theory',
between
'sage.matrix',
and
'sage.media',
As noted above, you should also read Producing Patches with Mercurial for information about how to do this in a copy of the Sage library and how to disseminate your changes.
If a function requires an optional package, that function should fail gracefully—perhaps using a try-except block—when the optional package is not available, and should give a hint about how to install it. For example, typing sage -optional gives a list of all optional packages, so it might suggest to the user that they type that. The command optional_packages() from within Sage also returns this list.