To meet the goal of making Sage easy to read, maintain, and improve, all Python/Cython code that is included with Sage should adhere to the style conventions discussed in this chapter.
Follow the standard Python formatting rules when writing code for Sage, as explained at the following URLs:
In particular,
Use 4 spaces for indentation levels. Do not use tabs as they can result in indentation confusion. Most editors have a feature that will insert 4 spaces when the tab key is hit. Also, many editors will automatically search/replace leading tabs with 4 spaces.
Use all lowercase function names with words separated by underscores. For example, you are encouraged to write Python functions using the naming convention
def set_some_value()
instead of the CamelCase convention
def SetSomeValue()
Use CamelCase for class names and major functions that create objects, e.g. PolynomialRing.
Note, however, that some functions do have uppercase letters where it makes sense. For instance, the function for lattice reduction by the LLL algorithm is called Matrix_integer_dense.LLL.
Python Sage library code uses the following conventions. Directory names may be plural (e.g. rings) and file names are almost always singular (e.g. polynomial_ring.py). Note that the file polynomial_ring.py might still contain definitions of several different types of polynomial rings.
For all of the conventions discussed here, you can find many examples in the Sage library. Browsing through the code is helpful, but so is searching: the functions search_src, search_def, and search_doc are worth knowing about. Briefly, from the “sage:” prompt, search_src(string) searches Sage library code for the string string. The command search_def(string) does a similar search, but restricted to function definitions, while search_doc(string) searches the Sage documentation. See their docstrings for more information and more options.
The top of each Sage code file should follow this format:
r"""
<Very short 1-line summary>
<Paragraph description>
...
AUTHORS:
- YOUR NAME (2005-01-03): initial version
- person (date in ISO year-month-day format): short desc
...
- person (date in ISO year-month-day format): short desc
...
Lots and lots of examples.
"""
#*****************************************************************************
# Copyright (C) 2008 YOUR NAME <your email>
#
# Distributed under the terms of the GNU General Public License (GPL)
# http://www.gnu.org/licenses/
#*****************************************************************************
The following is the top of the file
SAGE_ROOT/devel/sage/sage/rings/integer.pyx, which
contains the implementation for 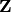 .
.
"""
Elements of the ring `\ZZ` of integers
AUTHORS:
- William Stein (2005): initial version
- Gonzalo Tornaria (2006-03-02): vastly improved python/GMP
conversion; hashing
- Didier Deshommes (2006-03-06): numerous examples
and docstrings
- William Stein (2006-03-31): changes to reflect GMP bug fixes
- William Stein (2006-04-14): added GMP factorial method (since it's
now very fast).
- David Harvey (2006-09-15): added nth_root, exact_log
- David Harvey (2006-09-16): attempt to optimise Integer constructor
- Rishikesh (2007-02-25): changed quo_rem so that the rem is positive
- David Harvey, Martin Albrecht, Robert Bradshaw (2007-03-01):
optimized Integer constructor and pool
- Pablo De Napoli (2007-04-01): multiplicative_order should return
+infinity for non zero numbers
- Robert Bradshaw (2007-04-12): is_perfect_power, Jacobi symbol (with
Kronecker extension). Convert some methods to use GMP directly
rather than pari, Integer(), PY_NEW(Integer)
- David Roe (2007-03-21): sped up valuation and is_square, added
val_unit, is_power, is_power_of and divide_knowing_divisible_by
- Robert Bradshaw (2008-03-26): gamma function, multifactorials
- Robert Bradshaw (2008-10-02): bounded squarefree part
EXAMPLES:
Add 2 integers::
sage: a = Integer(3) ; b = Integer(4)
sage: a + b == 7
True
Add an integer and a real number::
sage: a + 4.0
7.00000000000000
Add an integer and a rational number::
sage: a + Rational(2)/5
17/5
Add an integer and a complex number::
sage: b = ComplexField().0 + 1.5
sage: loads((a+b).dumps()) == a+b
True
::
sage: z = 32
sage: -z
-32
sage: z = 0; -z
0
sage: z = -0; -z
0
sage: z = -1; -z
1
Multiplication::
sage: a = Integer(3) ; b = Integer(4)
sage: a * b == 12
True
sage: loads((a * 4.0).dumps()) == a*b
True
sage: a * Rational(2)/5
6/5
::
sage: list([2,3]) * 4
[2, 3, 2, 3, 2, 3, 2, 3]
::
sage: 'sage'*Integer(3)
'sagesagesage'
COERCIONS: Returns version of this integer in the multi-precision
floating real field R.
::
sage: n = 9390823
sage: RR = RealField(200)
sage: RR(n)
9.3908230000000000000000000000000000000000000000000000000000e6
"""
#*****************************************************************************
# Copyright (C) 2004,2006 William Stein <wstein@gmail.com>
# Copyright (C) 2006 Gonzalo Tornaria <tornaria@math.utexas.edu>
# Copyright (C) 2006 Didier Deshommes <dfdeshom@gmail.com>
# Copyright (C) 2007 David Harvey <dmharvey@math.harvard.edu>
# Copyright (C) 2007 Martin Albrecht <malb@informatik.uni-bremen.de>
# Copyright (C) 2007,2008 Robert Bradshaw <robertwb@math.washington.edu>
# Copyright (C) 2007 David Roe <roed314@gmail.com>
#
# Distributed under the terms of the GNU General Public License (GPL)
# http://www.gnu.org/licenses/
#*****************************************************************************
All code included with Sage must be licensed under the GPLv2+ or a less restrictive license (e.g. the BSD license). It is very important that you include your name in the AUTHORS log so that everybody who submits code to Sage receives proper credit [2]. If ever you feel you are not receiving proper credit for anything you submit to Sage, please let the development team know!
Every function must have a docstring that includes the following information. Source files in the Sage library contain numerous examples on how to format your documentation, so you could use them as a guide.
A one-sentence description of the function, followed by a blank line.
An INPUT and an OUTPUT block for input and output arguments (see below for format). The type names should be descriptive, but do not have to represent the exact Sage/Python types. For example, use “integer” for anything that behaves like an integer; you do not have to put a precise type name such as int. The INPUT block describes the expected input to your function or method, while the OUTPUT block describes the expected output of the function/method. If appropriate, you need to describe any default values for the input arguments. For example:
INPUT:
- ``p`` -- (default: 2) a positive prime integer.
OUTPUT:
A 5-tuple consisting of integers in this order:
1. the smallest primitive root modulo p
2. the smallest prime primitive root modulo p
3. the largest primitive root modulo p
4. the largest prime primitive root modulo p
5. total number of prime primitive roots modulo p
Some people prefer to format their OUTPUT section as a block by using a dash. That is acceptable as well:
OUTPUT:
- The plaintext resulting from decrypting the ciphertext ``C``
using the Blum-Goldwasser decryption algorithm.
Instead of INPUT and OUTPUT blocks, you can include descriptions of the arguments and output using Sphinx/ReST markup, as described in http://sphinx.pocoo.org/markup/desc.html#info-field-lists. See below for an example.
An EXAMPLES block for examples. This is not optional. These examples are used for automatic testing before each release and new functions without these doctests will not be accepted for inclusion with Sage.
An ALGORITHM block (optional) which indicates what software and/or what algorithm is used. For example ALGORITHM: Uses Pari. Here’s a longer example that describes an algorithm used. Note that it also cites the reference where this algorithm can be found:
ALGORITHM:
The following algorithm is adapted from page 89 of [Nat2000]_.
Let `p` be an odd (positive) prime and let `g` be a generator
modulo `p`. Then `g^k` is a generator modulo `p` if and only if
`\gcd(k, p-1) = 1`. Since `p` is an odd prime and positive, then
`p - 1` is even so that any even integer between 1 and `p - 1`,
inclusive, is not relatively prime to `p - 1`. We have now
narrowed our search to all odd integers `k` between 1 and `p - 1`,
inclusive.
So now start with a generator `g` modulo an odd (positive) prime
`p`. For any odd integer `k` between 1 and `p - 1`, inclusive,
`g^k` is a generator modulo `p` if and only if `\gcd(k, p-1) = 1`.
REFERENCES:
.. [Nat2000] M.B. Nathanson. Elementary Methods in Number Theory.
Springer, 2000.
You can also number the steps in your algorithm using the hash-dot symbol. This way, the actual numbering of the steps are automatically taken care of when you build the documentation:
ALGORITHM:
The Blum-Goldwasser decryption algorithm is described in Algorithm
8.56, page 309 of [MenezesEtAl1996]_. The algorithm works as follows:
#. Let `C` be the ciphertext `C = (c_1, c_2, \dots, c_t, x_{t+1})`.
Then `t` is the number of ciphertext sub-blocks and `h` is the
length of each binary string sub-block `c_i`.
#. Let `(p, q, a, b)` be the private key whose corresponding
public key is `n = pq`. Note that `\gcd(p, q) = ap + bq = 1`.
#. Compute `d_1 = ((p + 1) / 4)^{t+1} \bmod{(p - 1)}`.
#. Compute `d_2 = ((q + 1) / 4)^{t+1} \bmod{(q - 1)}`.
#. Let `u = x_{t+1}^{d_1} \bmod p`.
#. Let `v = x_{t+1}^{d_2} \bmod q`.
#. Compute `x_0 = vap + ubq \bmod n`.
#. For `i` from 1 to `t`, do:
#. Compute `x_i = x_{t-1}^2 \bmod n`.
#. Let `p_i` be the `h` least significant bits of `x_i`.
#. Compute `m_i = p_i \oplus c_i`.
#. The plaintext is `m = m_1 m_2 \cdots m_t`.
A NOTES block for special notes (optional). Include information such as purpose etc. A NOTES block should start with .. NOTE::. You can also use the lower-case version .. note::, but do not mix lower-case with upper-case. However, you are encouraged to use the upper-case version .. NOTE::. If you want to put anything within the NOTES block, you should indent it at least 4 spaces (no tabs). Here’s an example of a NOTES block:
.. NOTE::
You should note that this sentence is indented at least 4
spaces. Avoid tab characters as much as possible when
writing code or editing the Sage documentation. You should
follow Python conventions by using spaces only.
A WARNING block for critical information about your code. For example, the WARNING block might include information about when or under which conditions your code might break, or information that the user should be particularly aware of. A WARNING block should start with .. WARNING::. It can also be the lower-case form .. warning::. However, you are encouraged to use the upper-case form .. WARNING::. Here’s an example of a WARNING block:
.. WARNING::
Whenever you edit the Sage documentation, make sure that
the edited version still builds. That is, you need to ensure
that you can still build the HTML and PDF versions of the
updated documentation. If the edited documentation fails to
build, it is very likely that you would be requested to
change your patch.
A REFERENCES block to list books or papers (optional). This block serves a similar purpose to a list of references in a research paper, or a bibliography in a monograph. If your method, function or class uses an algorithm that can be found in a standard reference, you should list that reference under this block. The Sphinx/ReST markup for citations is described at http://sphinx.pocoo.org/rest.html#citations. See below for an example.
An AUTHORS block (optional, but encouraged for important functions, so users can see from the docstring who wrote it and therefore whom to contact if they have questions).
Use the following template when documenting functions. Note the indentation:
def point(self, x=1, y=2):
r"""
This function returns the point `(x^5,y)`.
INPUT:
- ``x`` - integer (default: 1) the description of the
argument x goes here. If it contains multiple lines, all
the lines after the first need to be indented.
- ``y`` - integer (default: 2) the ...
OUTPUT:
integer -- the ...
EXAMPLES:
This example illustrates ...
::
sage: A = ModuliSpace()
sage: A.point(2,3)
xxx
We now ...
::
sage: B = A.point(5,6)
sage: xxx
It is an error to ...::
sage: C = A.point('x',7)
Traceback (most recent call last):
...
TypeError: unable to convert x (=r) to an integer
NOTES:
This function uses the algorithm of [BCDT]_ to determine
whether an elliptic curve E over Q is modular.
...
REFERENCES:
.. [BCDT] Breuil, Conrad, Diamond, Taylor, "Modularity ...."
AUTHORS:
- William Stein (2005-01-03)
- First_name Last_name (yyyy-mm-dd)
"""
<body of the function>
If you used Sphinx/ReST markup for the arguments, the beginning of the docstring would look like this:
def point(self, x=1, y=2):
r"""
This function returns the point `(x^5,y)`.
:param x: the description of the argument x goes here.
If it contains multiple lines, all the lines after the
first need to be indented.
:type x: integer; default 1
:param y: the ...
:type y: integer; default 2
:returns: the ...
:rtype: integer, the return type
You are strongly encouraged to:
Use nice LaTeX formatting everywhere. If you use backslashes, either use double backslashes or place an “r” right before the first triple opening quote. For example,
def cos(x):
"""
Returns `\\cos(x)`.
"""
def sin(x):
r"""
Returns `\sin(x)`.
"""
You can also use the MATH block to format complicated mathematical expressions:
.. MATH::
\sum_{i=1}^{\infty} (a_1 a_2 \cdots a_i)^{1/i}
\leq
e \sum_{i=1}^{\infty} a_i
Note
In ReST documentation, you use backticks ` to mark LaTeX code to be typeset. In Sage docstrings, unofficially you may use dollar signs instead – “unofficially” means that it ought to work, but might be a little buggy. Thus `x^2 + y^2 = 1` and $x^2 + y^2 = 1$ should produce identical output, typeset in math mode.
LaTeX style: typeset standard rings and fields like the integers and the real numbers using the locally-defined macro \\Bold, as in \\Bold{Z} for the integers. This macro is defined to be ordinary bold-face \\mathbf by default, but users can switch to blackboard-bold \\mathbb and back on-the-fly by using latex.blackboard_bold(True) and latex.blackboard_bold(False).
The docstring will be available interactively (for the “def point...” example above, by typing “point?” at the “sage:” prompt) and also in the reference manual. When viewed interactively, LaTeX code has the backslashes stripped from it, so “\cos” will appear as “cos”.
Because of the dual role of the docstring, you need to strike a balance between readability (for interactive help) and using perfect LaTeX code (for the reference manual). For instance, instead of using “\frac{a}{b}”, use “a/b” or maybe “a b^{-1}”. Also keep in mind that some users of Sage are not familiar with LaTeX; this is another reason to avoid complicated LaTeX expressions in docstrings, if at all possible: “\frac{a}{b}” will be obscure to someone who doesn’t know any LaTeX.
Finally, a few non-standard LaTeX macros are available to help achieve this balance, including “\ZZ”, “\RR”, “\CC”, and “\QQ”. These are names of Sage rings, and they are typeset using a single boldface character; they allow the use of “\ZZ” in a docstring, for example, which will appear interactively as “ZZ” while being typeset as “\Bold{Z}” in the reference manual. Other examples are “\GF” and “\Zmod”, each of which takes an argument: “\GF{q}” is typeset as “\Bold{F}_{q}” and “\Zmod{n}” is typeset as “\Bold{Z}/n\Bold{Z}”. See the file $SAGE_ROOT/devel/sage/sage/misc/latex_macros.py for a full list and for details about how to add more macros.
Liberally describe what the examples do. Note that there must be a blank line after the example code and before the explanatory text for the next example (indentation is not enough).
Illustrate any exceptions raised by the function with examples, as given above. (It is an error to ...; In particular, use ...)
Include many examples. These are automatically tested on a regular basis, and are crucial for the quality and adaptability of Sage. Without such examples, small changes to one part of Sage that break something else might not go seen until much later when someone uses the system, which is unacceptable. Note that new functions without doctests will not be accepted for inclusion in Sage.
Warning
Functions whose names start with an underscore do not currently appear in the reference manual, so avoid putting crucial documentation in their docstrings. In particular, if you are defining a class, you might put a long informative docstring after the class definition, not for the __init__ method. For example, from the file SAGE_ROOT/devel/sage/sage/crypto/classical.py:
class HillCryptosystem(SymmetricKeyCryptosystem):
"""
Create a Hill cryptosystem defined by the `m` x `m` matrix space
over `\mathbf{Z} / N \mathbf{Z}`, where `N` is the alphabet size of
the string monoid ``S``.
INPUT:
- ``S`` - a string monoid over some alphabet
- ``m`` - integer `> 0`; the block length of matrices that specify
block permutations
OUTPUT:
- A Hill cryptosystem of block length ``m`` over the alphabet ``S``.
EXAMPLES::
sage: S = AlphabeticStrings()
sage: E = HillCryptosystem(S,3)
sage: E
Hill cryptosystem on Free alphabetic string monoid on A-Z of block length 3
"""
and so on, while the __init__ method starts like this:
def __init__(self, S, m):
"""
See ``HillCryptosystem`` for full documentation.
EXAMPLES::
...
"""
Note also that the first docstring is printed if users type “HillCryptosystem?” at the “sage:” prompt.
(Before Sage 3.4, the reference manual used to include methods starting with underscores, so you will probably find many examples in the code which don’t follow this advice...)
The code in the examples should pass automatic testing. This means that if the above code is in the file f.py (or f.sage), then sage -t f.py should not give any error messages. Testing occurs with full Sage preparsing of input within the standard Sage shell environment, as described in Sage preparsing. Important: The file f.py is not imported when running tests unless you have arranged that it be imported into your Sage environment, i.e. unless its functions are available when you start Sage using the sage command. For example, the function cdd_convert in the file SAGE_ROOT/devel/sage/sage/geometry/polyhedra.py includes an EXAMPLES block containing the following:
sage: from sage.geometry.polyhedra import cdd_convert
sage: cdd_convert(' 1 1 0 0')
[1, 1, 0, 0]
Sage does not know about the function cdd_convert by default, so it needs to be imported before it is tested. Hence the first line in the example.
The Python script SAGE_LOCAL/bin/sage-doctest implements documentation testing in Sage (see Automated testing for more details). When writing documentation, keep the following points in mind:
All input is preparsed before being passed to Python, e.g. 2/3 is replaced by Integer(2)/Integer(3), which evaluates to 2/3 as a rational instead of the Python int 0. For more information on preparsing, see Sage preparsing.
If a test outputs to a file, the file should be in a temporary directory. For example (taken from the file SAGE_ROOT/devel/sage/sage/plot/plot.py):
sage: fig.savefig(os.path.join(SAGE_TMP, 'test.png'))
Here fig.savefig is the function doing the saving, SAGE_TMP is a temporary directory—this variable will always be defined properly during automated testing—and os.path.join is the preferred way to construct a path from a directory and a file. It works more generally than a Unix-flavored construction like SAGE_TMP + '/test.png'. If you want to use SAGE_TMP in Sage code, not just in a doctest, then you need to import it. Search the Sage code for examples.
If a test line contains the text random, it is executed by sage-doctest but sage-doctest does not check that the output agrees with the output in the documentation string. For example, the docstring for the __hash__ method for CombinatorialObject in SAGE_ROOT/devel/sage/sage/combinat/combinat.py includes the lines
sage: hash(c) #random
1335416675971793195
sage: c._hash #random
1335416675971793195
However, most functions generating pseudorandom output do not need this tag since the doctesting framework guarantees the state of the pseudorandom number generators (PRNGs) used in Sage for a given doctest. See Randomized testing for details on this framework.
If a line contains the text long time then that line is not tested unless the -long option is given, e.g. sage -t -long f.py. Use this to include examples that take more than about a second to run. These will not be run regularly during Sage development, but will get run before major releases. No example should take more than about 30 seconds.
For instance, here is part of the docstring from the regulator method for rational elliptic curves, from the file SAGE_ROOT/devel/sage/sage/schemes/elliptic_curves/ell_rational.py:
sage: E = EllipticCurve([0, 0, 1, -1, 0])
sage: E.regulator() # long time (1 second)
0.0511114082399688
If a line contains todo: not implemented, it is never tested. It is good to include lines like this to make clear what we want Sage to eventually implement:
sage: factor(x*y - x*z) # todo: not implemented
It is also immediately clear to the user that the indicated example does not currently work.
If a line contains the text optional, it is not tested unless the -optional flag is passed, e.g. sage -t -optional f.py. (Note that -optional must not be the first argument to sage.) Use this to include doctests that require optional packages. For example, the docstring for _magma_init_ in the class EllipticCurve_finite_field from the file SAGE_ROOT/devel/sage/sage/schemes/elliptic_curves/ell_finite_field.py contains
sage: E = EllipticCurve(GF(41),[2,5])
sage: E._magma_init_() # optional - requires Magma
'EllipticCurve([...|GF(41)!0,GF(41)!0,GF(41)!0,GF(41)!2,GF(41)!5])'
If the entire documentation string contains all three words optional, package, and installed, then the entire documentation string is not executed unless the -optional flag is passed to sage -t. This is useful for a long sequence of examples that all require that an optional package be installed.
Using search_src from the Sage prompt (or grep), one can easily find the aforementioned keywords. In the case of todo: not implemented, one can use the results of such a search to direct further development on Sage.
This section describes Sage’s automated testing of test files of the following types: .py, .pyx, .sage, .rst. Briefly, use sage -t <file> to test that the examples in <file> behave exactly as claimed. See the following subsections for more details. See also Documentation strings for a discussion on how to include examples in documentation strings and what conventions to follow. The chapter Parallel Testing the Sage Library contains a tutorial on doctesting modules in the Sage library.
Run sage -t <filename.py> to test all code examples in filename.py. Similar remarks apply to .sage and .pyx files.
sage -t [--verbose] [--optional] [files and directories ... ]
When you run sage -t <filename.py>, Sage makes a copy of <filename.py> with all the sage prompts replaced by >>>, then uses the standard Python doctest framework to test the documentation. More precisely, the Python script SAGE_LOCAL/bin/sage-doctest implements documentation testing. It does the following when asked to test a file foo.py or foo.sage.
Your file passes these tests if the code in it will run when entered at the sage: prompt with no special imports. Thus users are guaranteed to be able to exactly copy code out of the examples you write for the documentation and have them work.
Run sage -t <filename.rst> to test the examples in verbatim environments in ReST documentation. Sage creates a file .doctest_filename.py and tests it just as for .py, .pyx and .sage files.
Of course in ReST files, one often inserts explanatory texts between different verbatim environments. To link together verbatim environments, use the .. link:: comment. For example:
::
sage: a = 1
Next we add 1 to ``a``.
.. link::
::
sage: 1 + a
2
You can also put .. skip:: right before a verbatim environment to have that example skipped when testing the file. This goes right in the same place as the .. link:: in the previous example.
See the files in SAGE_ROOT/devel/sage/doc/en/tutorial/ for many examples of how to include automated testing in ReST documentation for Sage.
In addition to all the examples in your docstrings, which serve as both demonstrations and tests of your code, you should consider creating a test suite. Think of this as a program that will run for a while and “tries” to crash your code using randomly generated input. Your test code should define a class Test with a random() method that runs random tests. These are all assembled together later, and each test is run for a certain amount of time on a regular basis.
For example, see the file SAGE_ROOT/devel/sage/sage/modular/modsym/tests.py.
| [2] | See http://www.sagemath.org/development-map.html |