Representation theory

Ordinary characters

How can you compute character tables of a finite group in Sage? The Sage-GAP interface can be used to compute character tables.

You can construct the table of character values of a permutation group 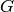as a Sage matrix, using the method character_table of the PermutationGroup class, or via the pexpect interface to the GAP command CharacterTable.

sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3,4)]])
sage: G.order()
8
sage: G.character_table()
[ 1  1  1  1  1]
[ 1 -1 -1  1  1]
[ 1 -1  1 -1  1]
[ 1  1 -1 -1  1]
[ 2  0  0  0 -2]
sage: CT = gap(G).CharacterTable()
sage: print gap.eval("Display(%s)"%CT.name())
CT1
<BLANKLINE>
 2  3  2  2  2  3
<BLANKLINE>
   1a 2a 2b 4a 2c
2P 1a 1a 1a 2c 1a
3P 1a 2a 2b 4a 2c
<BLANKLINE>
X.1     1  1  1  1  1
X.2     1 -1 -1  1  1
X.3     1 -1  1 -1  1
X.4     1  1 -1 -1  1
X.5     2  .  .  . -2

Here is another example:

sage: G = PermutationGroup([[(1,2),(3,4)], [(1,2,3)]])
sage: G.character_table()
[          1           1           1           1]
[          1           1  -zeta3 - 1       zeta3]
[          1           1       zeta3  -zeta3 - 1]
[          3          -1           0           0]
sage: gap.eval("G := Group((1,2)(3,4),(1,2,3))")
'Group([ (1,2)(3,4), (1,2,3) ])'
sage: gap.eval("T := CharacterTable(G)")
'CharacterTable( Alt( [ 1 .. 4 ] ) )'
sage: print gap.eval("Display(T)")
CT2
<BLANKLINE>
     2  2  2  .  .
     3  1  .  1  1
<BLANKLINE>
       1a 2a 3a 3b
    2P 1a 1a 3b 3a
    3P 1a 2a 1a 1a
<BLANKLINE>
X.1     1  1  1  1
X.2     1  1  A /A
X.3     1  1 /A  A
X.4     3 -1  .  .
<BLANKLINE>
A = E(3)^2
  = (-1-ER(-3))/2 = -1-b3

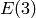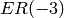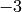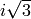where denotes a cube root of unity, denotes a square root of , say , and 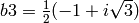. Note the added print Python command. This makes the output look much nicer.

sage: print gap.eval("irr := Irr(G)")
[ Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, 1, 1 ] ),
  Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, E(3)^2, E(3) ] ),
  Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, E(3), E(3)^2 ] ),
  Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 3, -1, 0, 0 ] ) ]
sage: print gap.eval("Display(irr)")
[ [       1,       1,       1,       1 ],
  [       1,       1,  E(3)^2,    E(3) ],
  [       1,       1,    E(3),  E(3)^2 ],
  [       3,      -1,       0,       0 ] ]
sage: gap.eval("CG := ConjugacyClasses(G)")
'[ ()^G, (1,2)(3,4)^G, (1,2,3)^G, (1,2,4)^G ]'
sage: gap.eval("gamma := CG[3]")
'(1,2,3)^G'
sage: gap.eval("g := Representative(gamma)")
'(1,2,3)'
sage: gap.eval("chi := irr[2]")
'Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, E(3)^2, E(3) ] )'
sage: gap.eval("g^chi")
'E(3)^2'

This last quantity is the value of the character chi at the group element g.

Alternatively, if you turn IPython “pretty printing” off, then the table prints nicely.

sage: %Pprint
Pretty printing has been turned OFF
sage: gap.eval("G := Group((1,2)(3,4),(1,2,3))")
'Group([ (1,2)(3,4), (1,2,3) ])'
sage: gap.eval("T := CharacterTable(G)")
'CharacterTable( Alt( [ 1 .. 4 ] ) )'
sage: gap.eval("Display(T)")
CT1

     2  2  2  .  .
     3  1  .  1  1

       1a 2a 3a 3b
    2P 1a 1a 3b 3a
    3P 1a 2a 1a 1a

X.1     1  1  1  1
X.2     1  1  A /A
X.3     1  1 /A  A
X.4     3 -1  .  .

A = E(3)^2
  = (-1-ER(-3))/2 = -1-b3
sage: gap.eval("irr := Irr(G)")
[ Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, 1, 1 ] ),
  Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, E(3)^2, E(3) ] ),
  Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 1, 1, E(3), E(3)^2 ] ),
  Character( CharacterTable( Alt( [ 1 .. 4 ] ) ), [ 3, -1, 0, 0 ] ) ]
sage: gap.eval("Display(irr)")
[ [       1,       1,       1,       1 ],
  [       1,       1,  E(3)^2,    E(3) ],
  [       1,       1,    E(3),  E(3)^2 ],
  [       3,      -1,       0,       0 ] ]
sage: %Pprint
Pretty printing has been turned ON

Brauer characters

The Brauer character tables in GAP do not yet have a “native” interface. To access them you can directly interface with GAP using pexpect and the gap.eval command.

The example below using the GAP interface illustrates the syntax.

sage: print gap.eval("G := Group((1,2)(3,4),(1,2,3))")
Group([ (1,2)(3,4), (1,2,3) ])
sage: print gap.eval("irr := IrreducibleRepresentations(G,GF(7))")   # random arch. dependent output
[ [ (1,2)(3,4), (1,2,3) ] -> [ [ [ Z(7)^0 ] ], [ [ Z(7)^4 ] ] ],
  [ (1,2)(3,4), (1,2,3) ] -> [ [ [ Z(7)^0 ] ], [ [ Z(7)^2 ] ] ],
  [ (1,2)(3,4), (1,2,3) ] -> [ [ [ Z(7)^0 ] ], [ [ Z(7)^0 ] ] ],
  [ (1,2)(3,4), (1,2,3) ] ->
    [ [ [ Z(7)^2, Z(7)^5, Z(7) ], [ Z(7)^3, Z(7)^2, Z(7)^3 ],
        [ Z(7), Z(7)^5, Z(7)^2 ] ],
      [ [ 0*Z(7), Z(7)^0, 0*Z(7) ], [ 0*Z(7), 0*Z(7), Z(7)^0 ],
        [ Z(7)^0, 0*Z(7), 0*Z(7) ] ] ] ]
sage: gap.eval("brvals := List(irr,chi->List(ConjugacyClasses(G),c->BrauerCharacterValue(Image(chi,Representative(c)))))")
''
sage: print gap.eval("Display(brvals)")              # random architecture dependent output
[ [       1,       1,  E(3)^2,    E(3) ],
  [       1,       1,    E(3),  E(3)^2 ],
  [       1,       1,       1,       1 ],
  [       3,      -1,       0,       0 ] ]
sage: print gap.eval("T := CharacterTable(G)")
CharacterTable( Alt( [ 1 .. 4 ] ) )
sage: print gap.eval("Display(T)")
CT3
<BLANKLINE>
     2  2  2  .  .
     3  1  .  1  1
<BLANKLINE>
       1a 2a 3a 3b
    2P 1a 1a 3b 3a
    3P 1a 2a 1a 1a
<BLANKLINE>
X.1     1  1  1  1
X.2     1  1  A /A
X.3     1  1 /A  A
X.4     3 -1  .  .
<BLANKLINE>
A = E(3)^2
  = (-1-ER(-3))/2 = -1-b3