Rings

Matrix rings

How do you construct a matrix ring over a finite ring in Sage? The MatrixSpace constructor accepts any ring as a base ring. Here’s an example of the syntax:

sage: R = IntegerModRing(51)
sage: M = MatrixSpace(R,3,3)
sage: M(0)
[0 0 0]
[0 0 0]
[0 0 0]
sage: M(1)
[1 0 0]
[0 1 0]
[0 0 1]
sage: 5*M(1)
[5 0 0]
[0 5 0]
[0 0 5]

Polynomial rings

How do you construct a polynomial ring over a finite field in Sage? Here’s an example:

sage: R = PolynomialRing(GF(97),'x')
sage: x = R.gen()
sage: f = x^2+7
sage: f in R
True

Here’s an example using the Singular interface:

sage: R = singular.ring(97, '(a,b,c,d)', 'lp')
sage: I = singular.ideal(['a+b+c+d', 'ab+ad+bc+cd', 'abc+abd+acd+bcd', 'abcd-1'])
sage: R
//   characteristic : 97
//   number of vars : 4
//        block   1 : ordering lp
//                  : names    a b c d
//        block   2 : ordering C
sage: I
a+b+c+d,
a*b+a*d+b*c+c*d,
a*b*c+a*b*d+a*c*d+b*c*d,
a*b*c*d-1

Here is another approach using GAP:

sage: R = gap.new("PolynomialRing(GF(97), 4)"); R
PolynomialRing( GF(97), ["x_1", "x_2", "x_3", "x_4"] )
sage: I = R.IndeterminatesOfPolynomialRing(); I
[ x_1, x_2, x_3, x_4 ]
sage: vars = (I.name(), I.name(), I.name(), I.name())
sage: _ = gap.eval("x_0 := %s[1];; x_1 := %s[2];; x_2 := %s[3];;\
...   x_3 := %s[4];;"%vars)
sage: f = gap.new("x_1*x_2+x_3"); f
x_2*x_3+x_4
sage: f.Value(I,[1,1,1,1])
Z(97)^34

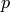-adic numbers

How do you construct 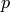-adics in Sage? A great deal of progress has been made on this (see SageDays talks by David Harvey and David Roe). Here only a few of the simplest examples are given.

To compute the characteristic and residue class field of the ring Zp of integers of Qp, use the syntax illustrated by the folowing examples.

sage: K = Qp(3)
sage: K.residue_class_field()
Finite Field of size 3
sage: K.residue_characteristic()
3
sage: a = K(1); a
1 + O(3^20)
sage: 82*a
1 + 3^4 + O(3^20)
sage: 12*a
3 + 3^2 + O(3^21)
sage: a in K
True
sage: b = 82*a
sage: b^4
1 + 3^4 + 3^5 + 2*3^9 + 3^12 + 3^13 + 3^16 + O(3^20)

Quotient rings of polynomials

How do you construct a quotient ring in Sage?

We create the quotient ring , and demonstrate many basic functions with it.

sage: R = PolynomialRing(GF(97),'x')
sage: x = R.gen()
sage: S = R.quotient(x^3 + 7, 'a')
sage: a = S.gen()
sage: S
Univariate Quotient Polynomial Ring in a over Finite Field of size 97 with
modulus x^3 + 7
sage: S.is_field()
True
sage: a in S
True
sage: x in S
True
sage: S.polynomial_ring()
Univariate Polynomial Ring in x over Finite Field of size 97
sage: S.modulus()
x^3 + 7
sage: S.degree()
3

In Sage, in means that there is a “canonical coercion” into the ring. So the integer 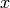and are both in 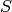, although 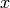really needs to be coerced.

You can also compute in quotient rings without actually computing then using the command quo_rem as follows.

sage: R = PolynomialRing(GF(97),'x')
sage: x = R.gen()
sage: f = x^7+1
sage: (f^3).quo_rem(x^7-1)
(x^14 + 4*x^7 + 7, 8)