How do I compute modular powers in Sage?
To compute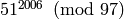 
in Sage, type
sage: R = Integers(97)
sage: a = R(51)
sage: a^2006
12
Instead of R = Integers(97) you can also type R = IntegerModRing(97). Another option is to use the interface with GMP:
sage: 51.powermod(99203843984,97)
96
To find a number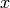 
such that
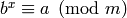(the discrete log of
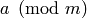), you can call ‘s log command:
sage: r = Integers(125)
sage: b = r.multiplicative_generator()^3
sage: a = b^17
sage: a.log(b)
17
This also works over finite fields:
sage: FF = FiniteField(16,"a")
sage: a = FF.gen()
sage: c = a^7
sage: c.log(a)
7
How do you construct prime numbers in Sage?
The class Primes allows for primality testing:
sage: 2^(2^12)+1 in Primes()
False
sage: 11 in Primes()
True
The usage of next_prime is self-explanatory:
sage: next_prime(2005)
2011
The Pari command primepi is used via the command
pari(x).primepi(). This returns the number of primes
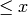, for example:
sage: pari(10).primepi()
4
Using primes_first_n or primes one can check that, indeed,
there are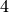 
primes up to 
:
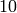sage: primes_first_n(5)
[2, 3, 5, 7, 11]
sage: list(primes(1, 10))
[2, 3, 5, 7]
How do you compute the sum of the divisors of an integer in Sage?
Sage uses divisors(n) for the number (usually denoted
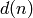) of divisors of 
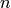and sigma(n,k) for the
sum of the 
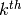powers of the divisors of 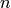(so
divisors(n) and sigma(n,0) are the same). For example:
sage: divisors(28); sum(divisors(28)); 2*28
[1, 2, 4, 7, 14, 28]
56
56
sage: sigma(28,0); sigma(28,1); sigma(28,2)
6
56
1050
Try this:
sage: Q = quadratic_residues(23); Q
[0, 1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18]
sage: N = [x for x in range(22) if kronecker(x,23)==-1]; N
[5, 7, 10, 11, 14, 15, 17, 19, 20, 21]
Q is the set of quadratic residues mod 23 and N is the set of non-residues.
Here is another way to construct these using the kronecker command (which is also called the “Legendre symbol”):
sage: [x for x in range(22) if kronecker(x,23)==1]
[1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18]
sage: [x for x in range(22) if kronecker(x,23)==-1]
[5, 7, 10, 11, 14, 15, 17, 19, 20, 21]