One of ‘s computational specialities is (the very technical field of) modular forms and can do a lot more than is even suggested in this very brief introduction.
How do you compute the dimension of a space of cusp forms using Sage?
To compute the dimension of the space of cusp forms for Gamma use the command dimension_cusp_forms. Here is an example from section “Modular forms” in the Tutorial:
sage: dimension_cusp_forms(Gamma0(11),2)
1
sage: dimension_cusp_forms(Gamma0(1),12)
1
sage: dimension_cusp_forms(Gamma1(389),2)
6112
Related commands: dimension_new__cusp_forms_gamma0 (for dimensions of newforms), dimension_modular_forms (for modular forms), and dimension_eis (for Eisenstein series). The syntax is similar - see the Reference Manual for examples.
In future versions of Sage, more related commands will be added.
The explicit representation of fundamental domains of arithmetic
quotients 
can be determined from the cosets of
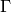in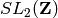 
. How are these cosets
computed in Sage?
Here is an example of computing the coset representatives of
:
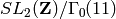sage: G = Gamma0(11); G
Congruence Subgroup Gamma0(11)
sage: list(G.coset_reps())
[[1 0]
[0 1],
[ 0 -1]
[ 1 0],
[1 0]
[1 1],
[ 0 -1]
[ 1 2],
[ 0 -1]
[ 1 3],
[ 0 -1]
[ 1 4],
[ 0 -1]
[ 1 5],
[ 0 -1]
[ 1 6],
[ 0 -1]
[ 1 7],
[ 0 -1]
[ 1 8],
[ 0 -1]
[ 1 9],
[ 0 -1]
[ 1 10]]
Next we illustrate computation of Hecke operators on a space of modular symbols of level 1 and weight 12.
sage: M = ModularSymbols(1,12)
sage: M.basis()
([X^8*Y^2,(0,0)], [X^9*Y,(0,0)], [X^10,(0,0)])
sage: t2 = M.T(2)
sage: f = t2.charpoly('x'); f
x^3 - 2001*x^2 - 97776*x - 1180224
sage: factor(f)
(x - 2049) * (x + 24)^2
sage: M.T(11).charpoly('x').factor()
(x - 285311670612) * (x - 534612)^2
Here t2 represents the Hecke operator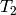 
on the space
of Full Modular Symbols for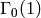 
of weight
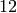with sign 
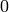and dimension 
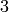over
.
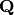sage: M = ModularSymbols(Gamma1(6),3,sign=0)
sage: M
Modular Symbols space of dimension 4 for Gamma_1(6) of weight 3 with sign 0
and over Rational Field
sage: M.basis()
([X,(0,5)], [X,(3,2)], [X,(4,5)], [X,(5,4)])
sage: M._compute_hecke_matrix_prime(2).charpoly()
x^4 - 17*x^2 + 16
sage: M.integral_structure()
Free module of degree 4 and rank 4 over Integer Ring
Echelon basis matrix:
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
See the section on modular forms in the Tutorial or the Reference Manual for more examples.
Sage can compute the genus of 
, 
,
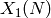and related curves. Here are some examples of the syntax:
sage: dimension_cusp_forms(Gamma0(22))
2
sage: dimension_cusp_forms(Gamma0(30))
3
sage: dimension_cusp_forms(Gamma1(30))
9
See the code for computing dimensions of spaces of modular forms (in sage/modular/dims.py) or the paper by Oesterlé and Cohen {CO} for some details.