See the Sage wiki page http://wiki.sagemath.org/graph_survey for an excellent survey of exisiting graph theory software.
Networkx (http://networkx.lanl.gov) “is a Python package for the creation, manipulation, and study of the structure, dynamics, and functions of complex networks”. More details can also be found on http://wiki.sagemath.org/graph_survey or in Robert Miller’s SageDays 3 talk.
sage: C = graphs.CubeGraph(4)
Now type C.show(vertex_labels=False, node_size=60, graph_border=True, figsize=[9,8]) to view this with some of the options.
The digraph below is a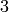 
-cycle with vertices
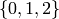and edges 
,
, 
:
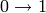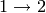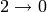sage: D = DiGraph( { 0: [1], 1: [2], 2: [0]} )
Type D.show() to view this.
includes wrappers to many NetworkX commands, written mainly by Emily Kirkman and Robert Miller. The implementation of Cayley graphs was written by Bobby Moretti and Robert Miller.
sage: G = DihedralGroup(5)
sage: C = G.cayley_graph(); C
Digraph on 10 vertices
sage: C.diameter()
3
sage: C.girth()
4
sage: C.automorphism_group().order()
10
sage: len(C.edges())
20
To construct the graph G with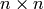 
adjacency
matrix 
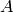, you want a graph 
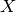so that the
vertex-set of G is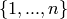 
, and ![[i,j]](_images/math/9467be6543ae7dfc59f1555f3f00952e4f3a00e6.png)
is an edge of G if and only if ![A[i][j] = 1](_images/math/81fd7de5e55f845fecf96f3690400a4e225a66a9.png)
.
Here is an example of the syntax in (copied from Robert Miller’s
SageDays 3 talk): Define the distance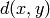 
from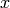 
to
to be the minimum length of a (directed) path in Gamma
joining a vertex 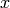to a vertex if such a path
exists, and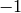 
otherwise.
A diameter of 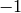is returned if G is not (strongly)
connected. Otherwise, the diameter of G is equal to the maximum
(directed) distance 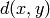in G (as 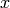and
range over all the vertices of G).
sage: M = Matrix ([ [0, 1, 1], [1, 0, 1], [1, 1, 0] ])
sage: # (the order is the number of edges)
sage: G = Graph(M); G.order()
3
sage: G.distance(0,2)
1
sage: G.diameter()
1