A linear code of length 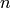 is a finite dimensional
subspace of
is a finite dimensional
subspace of 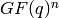 . Sage can compute with linear
error-correcting codes to a limited extent. It basically has some
wrappers to GAP and GUAVA 2.8 commands (GUAVA 2.8 does not include
any of Leon’s C code which was included in previous versions of
GUAVA). GUAVA 2.8 is included with Sage’s install of GAP 4.4.7 and
later.
. Sage can compute with linear
error-correcting codes to a limited extent. It basically has some
wrappers to GAP and GUAVA 2.8 commands (GUAVA 2.8 does not include
any of Leon’s C code which was included in previous versions of
GUAVA). GUAVA 2.8 is included with Sage’s install of GAP 4.4.7 and
later.
Sage can compute Hamming codes
sage: C = HammingCode(3,GF(3))
sage: C
Linear code of length 13, dimension 10 over Finite Field of size 3
sage: C.minimum_distance()
3
sage: C.gen_mat()
[1 0 0 0 0 0 0 0 2 0 0 2 1]
[0 1 0 0 0 0 0 0 2 0 0 2 0]
[0 0 1 0 0 0 0 0 2 0 0 2 2]
[0 0 0 1 0 0 0 0 2 0 0 1 0]
[0 0 0 0 1 0 0 0 2 0 0 1 2]
[0 0 0 0 0 1 0 0 2 0 0 1 1]
[0 0 0 0 0 0 1 0 2 0 0 0 2]
[0 0 0 0 0 0 0 1 2 0 0 0 1]
[0 0 0 0 0 0 0 0 0 1 0 2 2]
[0 0 0 0 0 0 0 0 0 0 1 2 1]
the four Golay codes
sage: C = ExtendedTernaryGolayCode()
sage: C
Linear code of length 12, dimension 6 over Finite Field of size 3
sage: C.minimum_distance()
6
sage: C.gen_mat()
[1 0 0 0 0 0 2 0 1 2 1 2]
[0 1 0 0 0 0 1 2 2 2 1 0]
[0 0 1 0 0 0 1 1 1 0 1 1]
[0 0 0 1 0 0 1 1 0 2 2 2]
[0 0 0 0 1 0 2 1 2 2 0 1]
[0 0 0 0 0 1 0 2 1 2 2 1]
as well as binary Reed-Muller codes, quadratic residue codes, quasi-quadratic residue codes, “random” linear codes, and a code generated by a matrix of full rank (using, as usual, the rows as the basis).
For a given code,  , Sage can return a generator matrix,
a check matrix, and the dual code:
, Sage can return a generator matrix,
a check matrix, and the dual code:
sage: C = HammingCode(3,GF(2))
sage: Cperp = C.dual_code()
sage: C; Cperp
Linear code of length 7, dimension 4 over Finite Field of size 2
Linear code of length 7, dimension 3 over Finite Field of size 2
sage: C.gen_mat()
[1 0 0 1 0 1 0]
[0 1 0 1 0 1 1]
[0 0 1 1 0 0 1]
[0 0 0 0 1 1 1]
sage: C.check_mat()
[1 0 0 1 1 0 1]
[0 1 0 1 0 1 1]
[0 0 1 1 1 1 0]
sage: C.dual_code()
Linear code of length 7, dimension 3 over Finite Field of size 2
sage: C = HammingCode(3,GF(4,'a'))
sage: C.dual_code()
Linear code of length 21, dimension 3 over Finite Field in a of size 2^2
For  and a vector
and a vector 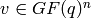 , Sage can try
to decode
, Sage can try
to decode  (i.e., find the codeword
(i.e., find the codeword 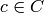 closest to
closest to  in the Hamming metric) using syndrome
decoding. As of yet, no special decoding methods have been
implemented.
in the Hamming metric) using syndrome
decoding. As of yet, no special decoding methods have been
implemented.
sage: C = HammingCode(3,GF(2))
sage: MS = MatrixSpace(GF(2),1,7)
sage: F = GF(2); a = F.gen()
sage: v1 = [a,a,F(0),a,a,F(0),a]
sage: C.decode(v1)
(1, 0, 0, 1, 1, 0, 1)
sage: v2 = matrix([[a,a,F(0),a,a,F(0),a]])
sage: C.decode(v2)
(1, 0, 0, 1, 1, 0, 1)
sage: v3 = vector([a,a,F(0),a,a,F(0),a])
sage: c = C.decode(v3); c
(1, 0, 0, 1, 1, 0, 1)
To plot the (histogram of) the weight distribution of a code, one can use the matplotlib package included with Sage:
sage: C = HammingCode(4,GF(2))
sage: C
Linear code of length 15, dimension 11 over Finite Field of size 2
sage: w = C.weight_distribution(); w
[1, 0, 0, 35, 105, 168, 280, 435, 435, 280, 168, 105, 35, 0, 0, 1]
sage: J = range(len(w))
sage: W = IndexedSequence([ZZ(w[i]) for i in J],J)
sage: P = W.plot_histogram()
Now type show(P) to view this.
There are several coding theory functions we are skipping entirely. Please see the reference manual or the file coding/linear_codes.py for examples.
Sage can also compute algebraic-geometric codes, called AG codes, via the Singular interface § sec:agcodes. One may also use the AG codes implemented in GUAVA via the Sage interface to GAP gap_console(). See the GUAVA manual for more details. {GUAVA}
A special type of stream cipher is implemented in Sage, namely, a linear feedback shift register (LFSR) sequence defined over a finite field. Stream ciphers have been used for a long time as a source of pseudo-random number generators. {linear feedback shift register}
S. Golomb {G} gives a list of three statistical properties a
sequence of numbers 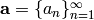 ,
,
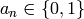 , should display to be considered “random”.
Define the autocorrelation of
, should display to be considered “random”.
Define the autocorrelation of 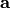 to be
to be
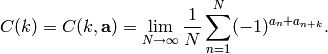
In the case where  is periodic with period
is periodic with period
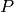 then this reduces to
then this reduces to
Assume  is periodic with period
is periodic with period 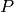 .
.
balance: 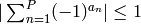 .
.
low autocorrelation:
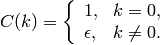
(For sequences satisfying these first two properties, it is known
that 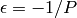 must hold.)
must hold.)
proportional runs property: In each period, half the runs have
length 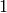 , one-fourth have length
, one-fourth have length 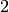 , etc.
Moveover, there are as many runs of
, etc.
Moveover, there are as many runs of 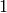 ‘s as there are of
‘s as there are of
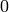 ‘s.
‘s.
A sequence satisfying these properties will be called pseudo-random. {pseudo-random}
A general feedback shift register is a map
 of the form
of the form
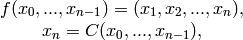
where 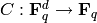 is a given
function. When
is a given
function. When  is of the form
is of the form
..math:: C(x_0,...,x_{n-1})=c_0x_0+...+c_{n-1}x_{n-1},
for some given constants 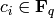 , the map is
called a linear feedback shift register (LFSR). The sequence of
coefficients
, the map is
called a linear feedback shift register (LFSR). The sequence of
coefficients 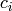 is called the key and the polynomial
is called the key and the polynomial
is sometimes called the connection polynomial.
Example: Over 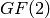 , if
, if
![[c_0,c_1,c_2,c_3]=[1,0,0,1]](_images/math/f9c7070a59d27a64f90fa880642929f399ddfc41.png) then
then
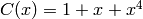 ,
,
The LFSR sequence is then
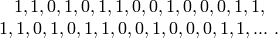
The sequence of 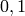 ‘s is periodic with period
‘s is periodic with period
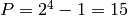 and satisfies Golomb’s three randomness
conditions. However, this sequence of period 15 can be “cracked”
(i.e., a procedure to reproduce
and satisfies Golomb’s three randomness
conditions. However, this sequence of period 15 can be “cracked”
(i.e., a procedure to reproduce  ) by knowing only 8
terms! This is the function of the Berlekamp-Massey algorithm {M},
implemented as lfsr_connection_polynomial (which produces the
reverse of berlekamp_massey).
) by knowing only 8
terms! This is the function of the Berlekamp-Massey algorithm {M},
implemented as lfsr_connection_polynomial (which produces the
reverse of berlekamp_massey).
sage: F = GF(2)
sage: o = F(0)
sage: l = F(1)
sage: key = [l,o,o,l]; fill = [l,l,o,l]; n = 20
sage: s = lfsr_sequence(key,fill,n); s
[1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0]
sage: lfsr_autocorrelation(s,15,7)
4/15
sage: lfsr_autocorrelation(s,15,0)
8/15
sage: lfsr_connection_polynomial(s)
x^4 + x + 1
sage: berlekamp_massey(s)
x^4 + x^3 + 1
has a type for cryptosystems (created by David Kohel, who also wrote the examples below), implementing classical cryptosystems. The general interface is as follows:
sage: S = AlphabeticStrings()
sage: S
Free alphabetic string monoid on A-Z
sage: E = SubstitutionCryptosystem(S)
sage: E
Substitution cryptosystem on Free alphabetic string monoid on A-Z
sage: K = S([ 25-i for i in range(26) ])
sage: e = E(K)
sage: m = S("THECATINTHEHAT")
sage: e(m)
GSVXZGRMGSVSZG
Here’s another example:
sage: S = AlphabeticStrings()
sage: E = TranspositionCryptosystem(S,15);
sage: m = S("THECATANDTHEHAT")
sage: G = E.key_space()
sage: G
Symmetric group of order 15! as a permutation group
sage: g = G([ 3, 2, 1, 6, 5, 4, 9, 8, 7, 12, 11, 10, 15, 14, 13 ])
sage: e = E(g)
sage: e(m)
EHTTACDNAEHTTAH
The idea is that a cryptosystem is a map
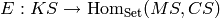 where
where
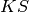 ,
, 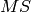 , and
, and  are the key space,
plaintext (or message) space, and ciphertext space, respectively.
are the key space,
plaintext (or message) space, and ciphertext space, respectively.
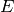 is presumed to be injective, so e.key() returns the
pre-image key.
is presumed to be injective, so e.key() returns the
pre-image key.