Linear Algebra

Sage provides standard constructions from linear algebra, e.g., the characteristic polynomial, echelon form, trace, decomposition, etc., of a matrix.

Creation of matrices and matrix multiplication is easy and natural:

sage: A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
sage: w = vector([1,1,-4])
sage: w*A
(0, 0, 0)
sage: A*w
(-9, 1, -2)
sage: kernel(A)
Free module of degree 3 and rank 1 over Integer Ring
Echelon basis matrix:
[ 1  1 -4]

Note that in Sage, the kernel of a matrix 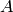is the “left kernel”, i.e. the space of vectors such that .

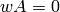Solving matrix equations is easy, using the method solve_right. Evaluating A.solve_right(Y) returns a matrix (or vector) 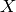so that :

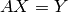sage: Y = vector([0, -4, -1])
sage: X = A.solve_right(Y)
sage: X
(-2, 1, 0)
sage: A * X   # checking our answer...
(0, -4, -1)

A backslash \ can be used in the place of solve_right; use A \ Y instead of A.solve_right(Y).

sage: A \ Y
(-2, 1, 0)

If there is no solution, Sage returns an error:

sage: A.solve_right(w)
...
ValueError: matrix equation has no solutions

Similarly, use A.solve_left(Y) to solve for 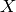in .

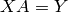Sage can also compute eigenvalues and eigenvectors:

sage: A = matrix([[0, 4], [-1, 0]])
sage: A.eigenvalues ()
[-2*I, 2*I]
sage: B = matrix([[1, 3], [3, 1]])
sage: B.eigenvectors_left()
[(4, [
(1, 1)
], 1), (-2, [
(1, -1)
], 1)]

(The syntax for the output of eigenvectors_left is a list of triples: (eigenvalue, eigenvector, multiplicity).) Eigenvalues and eigenvectors over QQ or RR can also be computed using Maxima (see Maxima below).

As noted in Basic Rings, the ring over which a matrix is defined affects some of its properties. In the following, the first argument to the matrix command tells Sage to view the matrix as a matrix of integers (the ZZ case), a matrix of rational numbers (QQ), or a matrix of reals (RR):

sage: AZ = matrix(ZZ, [[2,0], [0,1]])
sage: AQ = matrix(QQ, [[2,0], [0,1]])
sage: AR = matrix(RR, [[2,0], [0,1]])
sage: AZ.echelon_form()
[2 0]
[0 1]
sage: AQ.echelon_form()
[1 0]
[0 1]
sage: AR.echelon_form()
[ 1.00000000000000 0.000000000000000]
[0.000000000000000  1.00000000000000]

Matrix spaces

We create the space 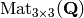of 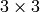matrices with rational entries:

sage: M = MatrixSpace(QQ,3)
sage: M
Full MatrixSpace of 3 by 3 dense matrices over Rational Field

(To specify the space of 3 by 4 matrices, you would use MatrixSpace(QQ,3,4). If the number of columns is omitted, it defaults to the number of rows, so MatrixSpace(QQ,3) is a synonym for MatrixSpace(QQ,3,3).) The space of matrices has a basis which Sage stores as a list:

sage: B = M.basis()
sage: len(B)
9
sage: B[1]
[0 1 0]
[0 0 0]
[0 0 0]

We create a matrix as an element of M.

sage: A = M(range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]

Next we compute its reduced row echelon form and kernel.

sage: A.echelon_form()
[ 1  0 -1]
[ 0  1  2]
[ 0  0  0]
sage: A.kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2  1]

Next we illustrate computation of matrices defined over finite fields:

sage: M = MatrixSpace(GF(2),4,8)
sage: A = M([1,1,0,0, 1,1,1,1, 0,1,0,0, 1,0,1,1,
...          0,0,1,0, 1,1,0,1, 0,0,1,1, 1,1,1,0])
sage: A
[1 1 0 0 1 1 1 1]
[0 1 0 0 1 0 1 1]
[0 0 1 0 1 1 0 1]
[0 0 1 1 1 1 1 0]
sage: rows = A.rows()
sage: A.columns()
[(1, 0, 0, 0), (1, 1, 0, 0), (0, 0, 1, 1), (0, 0, 0, 1),
 (1, 1, 1, 1), (1, 0, 1, 1), (1, 1, 0, 1), (1, 1, 1, 0)]
sage: rows
[(1, 1, 0, 0, 1, 1, 1, 1), (0, 1, 0, 0, 1, 0, 1, 1),
 (0, 0, 1, 0, 1, 1, 0, 1), (0, 0, 1, 1, 1, 1, 1, 0)]

We make the subspace over spanned by the above rows.

sage: V = VectorSpace(GF(2),8)
sage: S = V.subspace(rows)
sage: S
Vector space of degree 8 and dimension 4 over Finite Field of size 2
Basis matrix:
[1 0 0 0 0 1 0 0]
[0 1 0 0 1 0 1 1]
[0 0 1 0 1 1 0 1]
[0 0 0 1 0 0 1 1]
sage: A.echelon_form()
[1 0 0 0 0 1 0 0]
[0 1 0 0 1 0 1 1]
[0 0 1 0 1 1 0 1]
[0 0 0 1 0 0 1 1]

The basis of 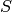used by Sage is obtained from the non-zero rows of the reduced row echelon form of the matrix of generators of .

Sparse Linear Algebra

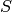Sage has support for sparse linear algebra over PIDs.

sage: M = MatrixSpace(QQ, 100, sparse=True)
sage: A = M.random_element(density = 0.05)
sage: E = A.echelon_form()

The multi-modular algorithm in Sage is good for square matrices (but not so good for non-square matrices):

sage: M = MatrixSpace(QQ, 50, 100, sparse=True)
sage: A = M.random_element(density = 0.05)
sage: E = A.echelon_form()
sage: M = MatrixSpace(GF(2), 20, 40, sparse=True)
sage: A = M.random_element()
sage: E = A.echelon_form()

Note that Python is case sensitive:

sage: M = MatrixSpace(QQ, 10,10, Sparse=True)
...
TypeError: MatrixSpace() got an unexpected keyword argument 'Sparse'