Conversion of symbolic expressions to other types¶

This module provides routines for converting new symbolic expressions to other types. Primarily, it provides a class Converter which will walk the expression tree and make calls to methods overridden by subclasses.

class sage.symbolic.expression_conversions.AlgebraicConverter(field)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

Convert a symbolic expression to an algebraic number.

EXAMPLES:

sage: from sage.symbolic.expression_conversions import AlgebraicConverter
sage: f = 2^(1/2)
sage: a = AlgebraicConverter(QQbar)
sage: a.arithmetic(f, f.operator())
1.414213562373095?

composition(ex, operator)¶

Coerce to an algebraic number.

EXAMPLES:

sage: from sage.symbolic.expression_conversions import AlgebraicConverter
sage: a = AlgebraicConverter(QQbar)
sage: a.composition(exp(I*pi/3), exp)
0.500000000000000? + 0.866025403784439?*I
sage: a.composition(sin(pi/5), sin)
0.5877852522924731? + 0.?e-18*I

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import AlgebraicConverter
sage: a = AlgebraicConverter(QQbar)
sage: f = SR(2)
sage: a.pyobject(f, f.pyobject())
2
sage: _.parent()
Algebraic Field

class sage.symbolic.expression_conversions.Converter(use_fake_div=False)¶

Bases: object

arithmetic(ex, operator)¶

The input to this method is a symbolic expression and the infix operator corresponding to that expression. Typically, one will convert all of the arguments and then perform the operation afterward.

TESTS:

sage: from sage.symbolic.expression_conversions import Converter
sage: f = x + 2
sage: Converter().arithmetic(f, f.operator())
...
NotImplementedError: arithmetic        

composition(ex, operator)¶

The input to this method is a symbolic expression and its operator. This method will get called when you have a symbolic function application.

TESTS:

sage: from sage.symbolic.expression_conversions import Converter
sage: f = sin(2)
sage: Converter().composition(f, f.operator())
...
NotImplementedError: composition        

derivative(ex, operator)¶

The input to this method is a symbolic expression which corresponds to a relation.

TESTS:

sage: from sage.symbolic.expression_conversions import Converter
sage: a = function('f', x).diff(x); a
D[0](f)(x)
sage: Converter().derivative(a, a.operator())
...
NotImplementedError: derivative

get_fake_div(ex)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import Converter
sage: c = Converter(use_fake_div=True)
sage: c.get_fake_div(sin(x)/x)
FakeExpression([sin(x), x], <built-in function div>)
sage: c.get_fake_div(-1*sin(x))
FakeExpression([sin(x)], <built-in function neg>)
sage: c.get_fake_div(-x)
FakeExpression([x], <built-in function neg>)
sage: c.get_fake_div((2*x^3+2*x-1)/((x-2)*(x+1)))
FakeExpression([2*x^3 + 2*x - 1, FakeExpression([x - 2, x + 1], <built-in function mul>)], <built-in function div>)

Check if #8056 is fixed, i.e., if numerator is 1.:

sage: c.get_fake_div(1/pi/x)
FakeExpression([1, FakeExpression([pi, x], <built-in function mul>)], <built-in function div>)

pyobject(ex, obj)¶

The input to this method is the result of calling pyobject() on a symbolic expression.

Note

Note that if a constant such as pi is encountered in the expression tree, its corresponding pyobject which is an instance of sage.symbolic.constants.Pi will be passed into this method. One cannot do arithmetic using such an object.

TESTS:

sage: from sage.symbolic.expression_conversions import Converter
sage: f = SR(1)
sage: Converter().pyobject(f, f.pyobject())
...
NotImplementedError: pyobject

relation(ex, operator)¶

The input to this method is a symbolic expression which corresponds to a relation.

TESTS:

sage: from sage.symbolic.expression_conversions import Converter
sage: import operator
sage: Converter().relation(x==3, operator.eq)
...
NotImplementedError: relation
sage: Converter().relation(x==3, operator.lt)
...
NotImplementedError: relation

symbol(ex)¶

The input to this method is a symbolic expression which corresponds to a single variable. For example, this method could be used to return a generator for a polynomial ring.

TESTS:

sage: from sage.symbolic.expression_conversions import Converter
sage: Converter().symbol(x)
...
NotImplementedError: symbol

class sage.symbolic.expression_conversions.FakeExpression(operands, operator)¶

Bases: object

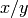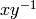Pynac represents $x/y$ as $xy^{-1}$ . Often, tree-walkers would prefer to see divisions instead of multiplications and negative exponents. To allow for this (since Pynac internally doesn’t have division at all), there is a possibility to pass use_fake_div=True; this will rewrite an Expression into a mixture of Expression and FakeExpression nodes, where the FakeExpression nodes are used to represent divisions. These nodes are intended to act sufficiently like Expression nodes that tree-walkers won’t care about the difference.

operands()¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import FakeExpression
sage: import operator; x,y = var('x,y')
sage: f = FakeExpression([x, y], operator.div)
sage: f.operands()
[x, y]

operator()¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import FakeExpression
sage: import operator; x,y = var('x,y')
sage: f = FakeExpression([x, y], operator.div)
sage: f.operator()
<built-in function div>

pyobject()¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import FakeExpression
sage: import operator; x,y = var('x,y')
sage: f = FakeExpression([x, y], operator.div)
sage: f.pyobject()
...
TypeError: self must be a numeric expression

class sage.symbolic.expression_conversions.FastCallableConverter(ex, etb)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

EXAMPLES:

sage: from sage.ext.fast_callable import ExpressionTreeBuilder
sage: etb = ExpressionTreeBuilder(vars=['x','y'])
sage: var('x,y')
(x, y)
sage: (x+y)._fast_callable_(etb)
add(v_0, v_1)
sage: (-x)._fast_callable_(etb)
neg(v_0)
sage: (x+y+x^2)._fast_callable_(etb)
add(add(ipow(v_0, 2), v_0), v_1)

TESTS:

Check if rational functions with numerator 1 can be converted. #8056:

sage: (1/pi/x)._fast_callable_(etb)
div(1, mul(pi, v_0))

sage: etb = ExpressionTreeBuilder(vars=['x'], domain=RDF)
sage: (x^7)._fast_callable_(etb)
ipow(v_0, 7)
sage: f(x)=1/pi/x; plot(f,2,3)

composition(ex, function)¶

Given an ExpressionTreeBuilder, return an Expression representing this value.

EXAMPLES:

sage: from sage.ext.fast_callable import ExpressionTreeBuilder
sage: etb = ExpressionTreeBuilder(vars=['x','y'])
sage: x,y = var('x,y')
sage: sin(sqrt(x+y))._fast_callable_(etb)
sin(sqrt(add(v_0, v_1)))
sage: arctan2(x,y)._fast_callable_(etb)
{arctan2}(v_0, v_1)

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.ext.fast_callable import ExpressionTreeBuilder
sage: etb = ExpressionTreeBuilder(vars=['x'])
sage: pi._fast_callable_(etb)
pi
sage: etb = ExpressionTreeBuilder(vars=['x'], domain=RDF)
sage: pi._fast_callable_(etb)
3.14159265359

relation(ex, operator)¶

EXAMPLES:

sage: ff = fast_callable(x == 2, vars=['x'])
sage: ff(2)
0
sage: ff(4)
2
sage: ff = fast_callable(x < 2, vars=['x'])
...
NotImplementedError

symbol(ex)¶

Given an ExpressionTreeBuilder, return an Expression representing this value.

EXAMPLES:

sage: from sage.ext.fast_callable import ExpressionTreeBuilder
sage: etb = ExpressionTreeBuilder(vars=['x','y'])
sage: x, y, z = var('x,y,z')
sage: x._fast_callable_(etb)
v_0
sage: y._fast_callable_(etb)
v_1
sage: z._fast_callable_(etb)
...
ValueError: Variable 'z' not found

class sage.symbolic.expression_conversions.FastFloatConverter(ex, *vars)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

EXAMPLES:

sage: x,y = var('x,y')
sage: f = x*x-y
sage: ff = f._fast_float_('x','y')
sage: ff(2,3)
1.0
    
sage: a = x + 2*y
sage: f = a._fast_float_('x', 'y')
sage: f(1,0)
1.0
sage: f(0,1)
2.0

sage: f = sqrt(x)._fast_float_('x'); f.op_list()
['load 0', 'call sqrt(1)']

sage: f = (1/2*x)._fast_float_('x'); f.op_list()
['load 0', 'push 0.5', 'mul']

composition(ex, operator)¶

EXAMPLES:

sage: f = sqrt(x)._fast_float_('x')
sage: f(2)
1.41421356237309...
sage: y = var('y')
sage: f = sqrt(x+y)._fast_float_('x', 'y')
sage: f(1,1)
1.41421356237309...

sage: f = sqrt(x+2*y)._fast_float_('x', 'y')
sage: f(2,0)
1.41421356237309...
sage: f(0,1)
1.41421356237309...

pyobject(ex, obj)¶

EXAMPLES:

sage: f = SR(2)._fast_float_()
sage: f(3)
2.0

relation(ex, operator)¶

EXAMPLES:

sage: ff = fast_float(x == 2, 'x')
sage: ff(2)
0.0
sage: ff(4)
2.0
sage: ff = fast_float(x < 2, 'x')
...
NotImplementedError

symbol(ex)¶

EXAMPLES:

sage: f = x._fast_float_('x', 'y')
sage: f(1,2)
1.0
sage: f = x._fast_float_('y', 'x')
sage: f(1,2)
2.0

class sage.symbolic.expression_conversions.InterfaceInit(interface)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

EXAMPLES:

sage: import operator
sage: from sage.symbolic.expression_conversions import InterfaceInit
sage: m = InterfaceInit(maxima)
sage: m.arithmetic(x+2, operator.add)
'(x)+(2)'

composition(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import InterfaceInit
sage: m = InterfaceInit(maxima)
sage: m.composition(sin(x), sin)
'sin(x)'
sage: m.composition(ceil(x), ceil)
'ceiling(x)'

sage: m = InterfaceInit(mathematica)
sage: m.composition(sin(x), sin)
'Sin[x]'        

derivative(ex, operator)¶

EXAMPLES:

sage: import operator
sage: from sage.symbolic.expression_conversions import InterfaceInit
sage: m = InterfaceInit(maxima)
sage: a = function('f', x).diff(x); a
D[0](f)(x)
sage: print m.derivative(a, a.operator())
diff('f(x), x, 1)
sage: b = function('f', x).diff(x).diff(x)
sage: print m.derivative(b, b.operator())
diff('f(x), x, 2)

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import InterfaceInit
sage: ii = InterfaceInit(gp)
sage: f = 2+I
sage: ii.pyobject(f, f.pyobject())
'I + 2'

sage: ii.pyobject(SR(2), 2)
'2'

sage: ii.pyobject(pi, pi.pyobject())
'Pi'

relation(ex, operator)¶

EXAMPLES:

sage: import operator
sage: from sage.symbolic.expression_conversions import InterfaceInit
sage: m = InterfaceInit(maxima)
sage: m.relation(x==3, operator.eq)
'x = 3'
sage: m.relation(x==3, operator.lt)
'x < 3'

symbol(ex)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import InterfaceInit
sage: m = InterfaceInit(maxima)
sage: m.symbol(x)
'x'
sage: f(x) = x
sage: m.symbol(f)
'x'

class sage.symbolic.expression_conversions.PolynomialConverter(ex, base_ring=None, ring=None)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

EXAMPLES:

sage: import operator
sage: from sage.symbolic.expression_conversions import PolynomialConverter

sage: x, y = var('x, y')
sage: p = PolynomialConverter(x, base_ring=RR)
sage: p.arithmetic(pi+e, operator.add)
5.85987448204884
sage: p.arithmetic(x^2, operator.pow)
x^2

sage: p = PolynomialConverter(x+y, base_ring=RR)
sage: p.arithmetic(x*y+y^2, operator.add)
x*y + y^2

composition(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import PolynomialConverter
sage: a = sin(2)
sage: p = PolynomialConverter(a*x, base_ring=RR)
sage: p.composition(a, a.operator())
0.909297426825682

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import PolynomialConverter
sage: p = PolynomialConverter(x, base_ring=QQ)
sage: f = SR(2)
sage: p.pyobject(f, f.pyobject())
2
sage: _.parent()
Rational Field

relation(ex, op)¶

EXAMPLES:

sage: import operator
sage: from sage.symbolic.expression_conversions import PolynomialConverter

sage: x, y = var('x, y')
sage: p = PolynomialConverter(x, base_ring=RR)

sage: p.relation(x==3, operator.eq)
x - 3.00000000000000
sage: p.relation(x==3, operator.lt)
...
ValueError: Unable to represent as a polynomial

sage: p = PolynomialConverter(x - y, base_ring=QQ)
sage: p.relation(x^2 - y^3 + 1 == x^3, operator.eq)
-x^3 - y^3 + x^2 + 1

symbol(ex)¶

Returns a variable in the polynomial ring.

EXAMPLES:

sage: from sage.symbolic.expression_conversions import PolynomialConverter
sage: p = PolynomialConverter(x, base_ring=QQ)
sage: p.symbol(x)
x
sage: _.parent()
Univariate Polynomial Ring in x over Rational Field

class sage.symbolic.expression_conversions.RingConverter(R, subs_dict=None)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import RingConverter
sage: P.<z> = ZZ[]
sage: R = RingConverter(P, subs_dict={x:z})
sage: a = 2*x^2 + x + 3
sage: R(a)
2*z^2 + z + 3

composition(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import RingConverter
sage: R = RingConverter(RIF)
sage: R(cos(2))
-0.4161468365471424?

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import RingConverter
sage: R = RingConverter(RIF)
sage: R(SR(5/2))
2.5000000000000000?

symbol(ex)¶

All symbols appearing in the expression must appear in subs_dict in order for the conversion to be successful.

EXAMPLES:

sage: from sage.symbolic.expression_conversions import RingConverter
sage: R = RingConverter(RIF, subs_dict={x:2})
sage: R(x+pi)
5.141592653589794?

sage: R = RingConverter(RIF)
sage: R(x+pi)
...
TypeError

class sage.symbolic.expression_conversions.SubstituteFunction(ex, original, new)¶

Bases: sage.symbolic.expression_conversions.Converter

arithmetic(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SubstituteFunction
sage: foo = function('foo'); bar = function('bar')
sage: s = SubstituteFunction(foo(x), foo, bar)
sage: f = x*foo(x) + pi/foo(x)
sage: s.arithmetic(f, f.operator())
x*bar(x) + pi/bar(x)

composition(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SubstituteFunction
sage: foo = function('foo'); bar = function('bar')
sage: s = SubstituteFunction(foo(x), foo, bar)
sage: f = foo(x)
sage: s.composition(f, f.operator())
bar(x)
sage: f = foo(foo(x))
sage: s.composition(f, f.operator())
bar(bar(x))
sage: f = sin(foo(x))
sage: s.composition(f, f.operator())
sin(bar(x))
sage: f = foo(sin(x))
sage: s.composition(f, f.operator())
bar(sin(x))

derivative(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SubstituteFunction
sage: foo = function('foo'); bar = function('bar')
sage: s = SubstituteFunction(foo(x), foo, bar)
sage: f = foo(x).diff(x)
sage: s.derivative(f, f.operator())
D[0](bar)(x)

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SubstituteFunction
sage: foo = function('foo'); bar = function('bar')
sage: s = SubstituteFunction(foo(x), foo, bar)
sage: f = SR(2)
sage: s.pyobject(f, f.pyobject())
2
sage: _.parent()
Symbolic Ring

relation(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SubstituteFunction
sage: foo = function('foo'); bar = function('bar')
sage: s = SubstituteFunction(foo(x), foo, bar)
sage: eq = foo(x) == x
sage: s.relation(eq, eq.operator())
bar(x) == x

symbol(ex)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SubstituteFunction
sage: foo = function('foo'); bar = function('bar')
sage: s = SubstituteFunction(foo(x), foo, bar)
sage: s.symbol(x)
x

class sage.symbolic.expression_conversions.SympyConverter(use_fake_div=False)¶

Bases: sage.symbolic.expression_conversions.Converter

Converts any expression to SymPy.

EXAMPLE:

sage: import sympy
sage: var('x,y')
(x, y)
sage: f = exp(x^2) - arcsin(pi+x)/y
sage: f._sympy_()
-asin(pi + x)/y + exp(x**2)
sage: _._sage_()
-arcsin(pi + x)/y + e^(x^2)

sage: sympy.sympify(x) # indirect doctest
x    

arithmetic(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SympyConverter
sage: s = SympyConverter()
sage: f = x + 2
sage: s.arithmetic(f, f.operator())
2 + x

composition(ex, operator)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SympyConverter
sage: s = SympyConverter()
sage: f = sin(2)
sage: s.composition(f, f.operator())
sin(2)
sage: type(_)
sin
sage: f = arcsin(2)
sage: s.composition(f, f.operator())
asin(2)

pyobject(ex, obj)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SympyConverter
sage: s = SympyConverter()
sage: f = SR(2)
sage: s.pyobject(f, f.pyobject())
2
sage: type(_)
<class 'sympy.core.numbers.Integer'>

symbol(ex)¶

EXAMPLES:

sage: from sage.symbolic.expression_conversions import SympyConverter
sage: s = SympyConverter()
sage: s.symbol(x)
x
sage: type(_)
<class 'sympy.core.symbol.Symbol'>

sage.symbolic.expression_conversions.algebraic(ex, field)¶

Returns the symbolic expression ex as a element of the algebraic field field.

EXAMPLES:

sage: a = SR(5/6)
sage: AA(a)
5/6
sage: type(AA(a))
<class 'sage.rings.qqbar.AlgebraicReal'>
sage: QQbar(a)
5/6
sage: type(QQbar(a))
<class 'sage.rings.qqbar.AlgebraicNumber'>
sage: QQbar(i)
1*I
sage: AA(golden_ratio)
1.618033988749895?
sage: QQbar(golden_ratio)
1.618033988749895?
sage: QQbar(sin(pi/3))
0.866025403784439?

sage: QQbar(sqrt(2) + sqrt(8))
4.242640687119285?
sage: AA(sqrt(2) ^ 4) == 4
True
sage: AA(-golden_ratio)
-1.618033988749895?
sage: QQbar((2*I)^(1/2))
1 + 1*I
sage: QQbar(e^(pi*I/3))
0.500000000000000? + 0.866025403784439?*I

sage: AA(x*sin(0))
0
sage: QQbar(x*sin(0))
0

sage.symbolic.expression_conversions.fast_callable(ex, etb)¶

Given an ExpressionTreeBuilder etb, return an Expression representing the symbolic expression ex.

EXAMPLES:

sage: from sage.ext.fast_callable import ExpressionTreeBuilder
sage: etb = ExpressionTreeBuilder(vars=['x','y'])
sage: x,y = var('x,y')
sage: f = y+2*x^2
sage: f._fast_callable_(etb)
add(mul(ipow(v_0, 2), 2), v_1)

sage: f = (2*x^3+2*x-1)/((x-2)*(x+1))
sage: f._fast_callable_(etb)
div(add(add(mul(ipow(v_0, 3), 2), mul(v_0, 2)), -1), mul(add(v_0, -2), add(v_0, 1)))

sage.symbolic.expression_conversions.fast_float(ex, *vars)¶

Returns an object which provides fast floating point evaluation of the symbolic expression ex.

See sage.ext.fast_eval for more information.

EXAMPLES:

sage: from sage.symbolic.expression_conversions import fast_float
sage: f = sqrt(x+1)
sage: ff = fast_float(f, 'x')
sage: ff(1.0)
1.4142135623730951

sage.symbolic.expression_conversions.polynomial(ex, base_ring=None, ring=None)¶

Returns a polynomial from the symbolic expression ex. Either a base ring base_ring or a polynomial ring ring can be specified for the parent of result. If just a base ring is given, then the variables of the base ring will be the variables of the expression ex.

EXAMPLES:

sage: from sage.symbolic.expression_conversions import polynomial
sage: f = x^2 + 2
sage: polynomial(f, base_ring=QQ)
x^2 + 2
sage: _.parent()
Univariate Polynomial Ring in x over Rational Field

sage: polynomial(f, ring=QQ['x,y'])
x^2 + 2
sage: _.parent()
Multivariate Polynomial Ring in x, y over Rational Field

sage: x, y = var('x, y')
sage: polynomial(x + y^2, ring=QQ['x,y'])
y^2 + x
sage: _.parent()
Multivariate Polynomial Ring in x, y over Rational Field

sage: s,t=var('s,t')
sage: expr=t^2-2*s*t+1
sage: expr.polynomial(None,ring=SR['t'])
t^2 - 2*s*t + 1
sage: _.parent()
Univariate Polynomial Ring in t over Symbolic Ring

The polynomials can have arbitrary (constant) coefficients so long as they coerce into the base ring:

sage: polynomial(2^sin(2)*x^2 + exp(3), base_ring=RR)
1.87813065119873*x^2 + 20.0855369231877

Conversion of symbolic expressions to other types¶

Previous topic

Next topic

This Page

Navigation

Conversion of symbolic expressions to other types¶

Previous topic

Next topic

This Page

Quick search

Navigation